如何理解泊松分布
文章目录
- 一、引例——鲸鱼研究
- 二、泊松分布
一、引例——鲸鱼研究
有生态学家对生活在北冰洋水域的鲸鱼进行了跟踪研究,他们利用一台水下无人机来探测鲸鱼数量,这是近十天的数据:
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | 第9天 | 第10天 |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 10 | 14 | 12 | 11 | 15 | 8 | 9 | 7 | 6 |
最后四天鲸鱼数目的连续减少趋势令人担忧,水质恶化吗?。
注意到每天探测到的鲸鱼不会是同时发生的,而是分散在一天的不同时间段。
这事实上是一个随机事件的时间分布,于是我们将一天时间划分为12段,那么第一天的数据如下:

那么对于这组数据,鲸鱼出现的概率 p = 5/6
我们试图把鱼群数量转换成时间上的二项分布,那么 12 个 时间段就转化成了一个二项分布,一天内出现10头鲸鱼的概率如下:
Cnk⋅pk⋅(1−p)n−k=C1210⋅(56)10⋅(16)2=0.2961C_n^k \cdot p^k \cdot (1-p)^{n-k} = C_{12}^{10} \cdot (\frac{5}{6})^{10} \cdot (\frac{1}{6})^2 = 0.2961 Cnk⋅pk⋅(1−p)n−k=C1210⋅(65)10⋅(61)2=0.2961
这正是 拉普拉斯 得意门生 西莫恩·德尼·泊松(1781~1840) 的思路。
前面我们选取的是第一天的数据,我们现在选取第二天的数据,有14头鲸鱼,12个时间段有些不够用,于是我们划分成24个时间段。

则一天中出现14头鲸鱼的概率:
pi=1424=712则Cnk⋅pk⋅(1−p)n−k=C2414⋅(712)14⋅(512)10=0.1634\begin{align} & p_i = \frac{14}{24} = \frac{7}{12} & 则 C_n^k \cdot p^k \cdot (1-p)^{n-k} = C_{24}^{14} \cdot (\frac{7}{12})^{14} \cdot (\frac{5}{12})^{10} = 0.1634 \end{align} pi=2414=127则Cnk⋅pk⋅(1−p)n−k=C2414⋅(127)14⋅(125)10=0.1634
但是我们上面的思考有一个漏洞就:一个时间段是有可能有多头鲸鱼出现的
这说明什么?时间段太大了!我们直接把一天划分成无数个时间段,单独每个时间段都趋于无穷小,这样无论两头鲸鱼的时间挨得有多近,都能区分开来,则有:
limn→∞Cnk⋅pk⋅(1−p)n−k,其中:n代表时间分段数,p代表任意时间段内鲸鱼出现的概率p的估计不再以某一天数据为准,而是选取平均值,即p=μn\begin{align} & lim_{n \rightarrow \infty} C_n^k \cdot p^k \cdot (1-p)^{n-k},其中:\\ & n代表时间分段数,p代表任意时间段内鲸鱼出现的概率 \\ & p的估计不再以某一天数据为准,而是选取平均值,即 p = \frac{\mu}{n} \end{align} limn→∞Cnk⋅pk⋅(1−p)n−k,其中:n代表时间分段数,p代表任意时间段内鲸鱼出现的概率p的估计不再以某一天数据为准,而是选取平均值,即p=nμ
公式的进一步推导:
limn→∞Cnk⋅pk⋅(1−p)n−k=limn→∞Cnk⋅(μn)k⋅(1−μn)n−k=limn→∞n(n−1)(n−2)⋯(n−k+1)k!⋅μknk⋅(1−μn)n−k=μkk!⋅limn→∞n(n−1)(n−2)⋯(n−k+1)nk⋅(1−μn)n−k=μkk!⋅limn→∞nn(n−1)n(n−2)n⋯(n−k+1)n⋅(1−μn)n−k=μkk!⋅limn→∞1⋅1…1⋅(1−μn)n−k=μkk!⋅limn→∞(1−μn)n−k=μkk!⋅limn→∞(1−μn)n⋅limn→∞(1−μn)−k=μkk!⋅limn→∞(1−μn)n=μkk!e−μ(等价无穷小)\begin{align} & lim_{n \rightarrow \infty} C_n^k \cdot p^k \cdot (1-p)^{n-k} \\ =& lim_{n \rightarrow \infty} C_n^k \cdot (\frac{\mu}{n})^k \cdot (1-\frac{\mu}{n})^{n-k} \\ =& \lim _{n \rightarrow \infty} \frac{n(n-1)(n-2) \cdots(n-k+1)}{k!} \cdot \frac{\mu^{k}}{n^{k}} \cdot\left(1-\frac{\mu}{n}\right)^{n-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} \frac{n(n-1)(n-2) \cdots(n-k+1)}{n^{k}} \cdot\left(1-\frac{\mu}{n}\right)^{n-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} \frac{n}{n} \frac{(n-1)}{n} \frac{(n-2)}{n} \cdots \frac{(n-k+1)}{n} \cdot\left(1-\frac{\mu}{n}\right)^{n-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} 1 \cdot 1 \dots 1 \cdot\left(1-\frac{\mu}{n}\right)^{n-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} \left(1-\frac{\mu}{n}\right)^{n-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} \left(1-\frac{\mu}{n}\right)^{n} \cdot \lim _{n \rightarrow \infty} \left(1-\frac{\mu}{n}\right)^{-k} \\ =& \frac{\mu^{k}}{k!} \cdot \lim _{n \rightarrow \infty} \left(1-\frac{\mu}{n}\right)^{n} \\ =& \frac{\mu^{k}}{k!} e^{-\mu} (等价无穷小) \\ \end{align} =========limn→∞Cnk⋅pk⋅(1−p)n−klimn→∞Cnk⋅(nμ)k⋅(1−nμ)n−kn→∞limk!n(n−1)(n−2)⋯(n−k+1)⋅nkμk⋅(1−nμ)n−kk!μk⋅n→∞limnkn(n−1)(n−2)⋯(n−k+1)⋅(1−nμ)n−kk!μk⋅n→∞limnnn(n−1)n(n−2)⋯n(n−k+1)⋅(1−nμ)n−kk!μk⋅n→∞lim1⋅1…1⋅(1−nμ)n−kk!μk⋅n→∞lim(1−nμ)n−kk!μk⋅n→∞lim(1−nμ)n⋅n→∞lim(1−nμ)−kk!μk⋅n→∞lim(1−nμ)nk!μke−μ(等价无穷小)
二、泊松分布
我们把上面的μ 换成 λ,就得到了我们熟悉的泊松分布公式:
λkk!e−λ,其中λ代表给定时间段或空间区域内,随机事件平均发生的次数。\frac{\lambda^k}{k!}e^{-\lambda},其中 \lambda 代表给定时间段或空间区域内,随机事件平均发生的次数。 k!λke−λ,其中λ代表给定时间段或空间区域内,随机事件平均发生的次数。
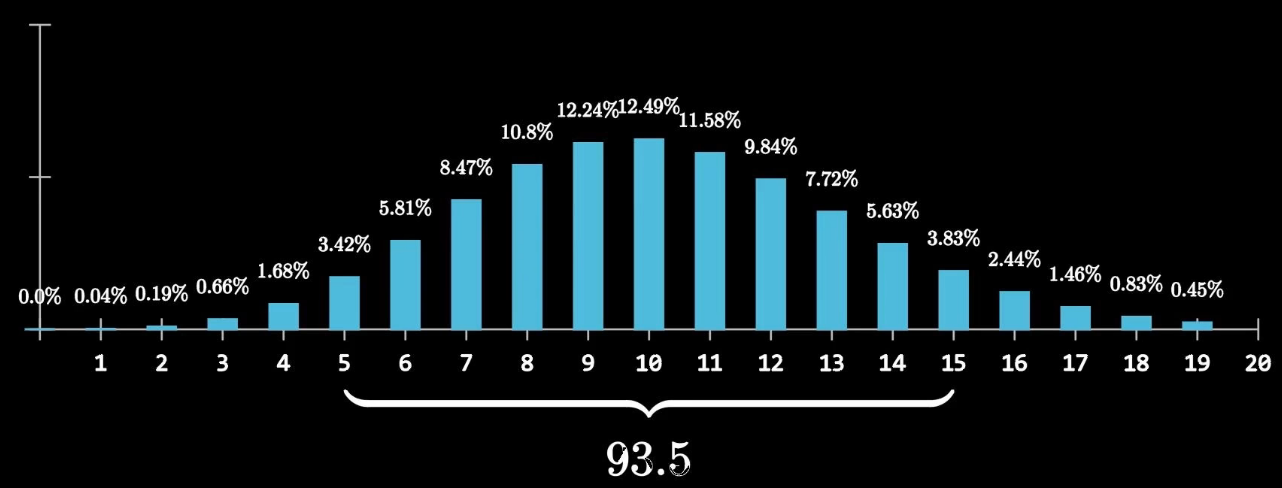
我们利用该公式计算引例中各时间段鲸鱼出现数目的可能性,并用柱状图来表示:
我们取显著性水平为 6.5%,那么从图中可以得知,鲸鱼数目在[5, 15]都是正常范围,我们的样本都在正常范围内。
有时候我们会用用泊松分布近似二项分布,一般在 试验次数n 很大,成功概率 p 很小,且 λ = np 为有限值时,二项分布可以用泊松分布来近似,经过前面的推导,不难明白其中缘由。