零基础-动手学深度学习-6.1 从全连接层到卷积
基于卷积神经网络架构的模型在计算机视觉领域中已经占主导地位,在本章的开始,我们将介绍构成所有卷积网络主干的基本元素。 这包括卷积层本身、填充(padding)和步幅(stride)的基本细节、用于在相邻区域汇聚信息的汇聚层(pooling)、在每一层中多通道(channel)的使用,以及有关现代卷积网络架构的仔细讨论。
先前讨论的MLP适合处理表格数据,行列对应的样本和特征,然而对于高维感知的数据并不适用。
尤其是想一下要是百万级的像素图片输入,直接用全连接层哪怕是降维到1000(这样的话效果还不是很好),需要的参数也是上亿级别的,拟合这样的参数还需要收集大量的数据,因此我们需要卷积。
6.1.1. 不变性
假设我们想从一张图片中找到某个物体。 合理的假设是:无论哪种方法找到这个物体,都应该和物体的位置无关,因此我们可以使用一个“沃尔多检测器”扫描图像。 该检测器将图像分割成多个区域,并为每个区域包含沃尔多的可能性打分。 卷积神经网络正是将空间不变性的这一概念系统化,从而基于这个模型使用较少的参数来学习有用的表示。
现在,我们将上述想法总结一下,从而帮助我们设计适合于计算机视觉的神经网络架构。
平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
让我们看看这些原则是如何转化为数学表示的。
6.1.2. 多层感知机的限制

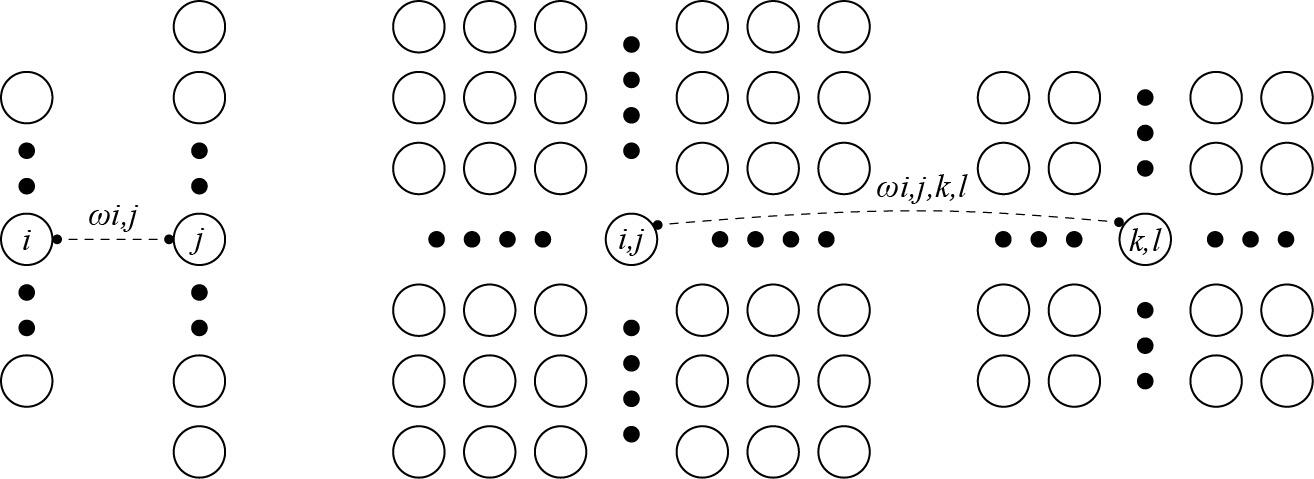
这里好像是有点难以理解?可以看下面的图示,针对于原本只有长度维度的向量输入的全连接层的变换如下图左边所示,输入i变化成输出j维度,其中权重为wij,然而对于有高度宽度的的输入向量xij,我们自然要用四阶的权重张量来连接,可以得到第一个式子,就是x遍布kl得到ij的全连接,这个时候为了方便观察,我们修改权重索引,让k=i+a,l=j+b,这样我们就可以发现通过索引ab可以在基于ij的正偏移和负偏移下去覆盖这整个图像,对于隐藏表示输出Hij我们可以理解为对输入Xij为中心进行v的加权求和得到的结果。
 下一步就是把平移不变性和局部性运用进去:
下一步就是把平移不变性和局部性运用进去:
1.平移不变性需要X无论怎么偏移都可以识别出来,因此即是输出和权重不能依赖于ij的值,那么这个时候卷积的概念已经出来了,我们将使用权重Vab对位置ij附近的像素i+a,j+b进行加权以得到Hij输出,这个时候我们发现权重也变小了,一石二鸟。
2.局部性,太远的像素之间关联不要,那么只要限制ab取值就行。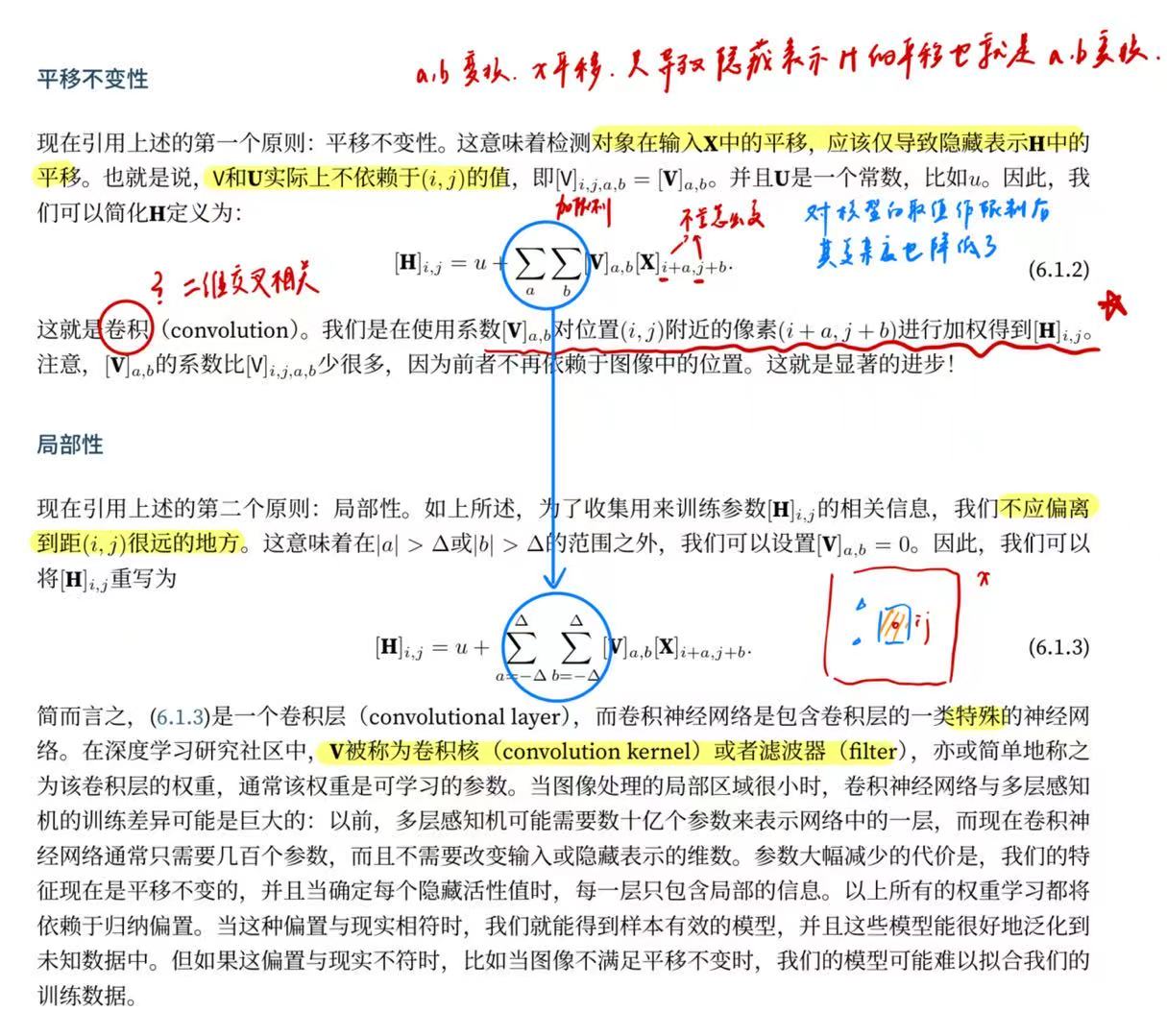
上面的说完书上还讲了一些卷积的基本定义,很简单就不说了,下面还有个通道:
 然而,仍有许多问题亟待解决。 例如,图像中是否到处都有存在沃尔多的可能?如何有效地计算输出层?如何选择适当的激活函数?为了训练有效的网络,如何做出合理的网络设计选择?我们将在本章的其它部分讨论这些问题。
然而,仍有许多问题亟待解决。 例如,图像中是否到处都有存在沃尔多的可能?如何有效地计算输出层?如何选择适当的激活函数?为了训练有效的网络,如何做出合理的网络设计选择?我们将在本章的其它部分讨论这些问题。
