188.买卖股票的最佳时机IV 309.最佳买卖股票时机含冷冻期 714.买卖股票的最佳时机含手续费
LeetCode 188.买卖股票的最佳时机IV
思路：
与买卖股票的最佳时机III的差不多，前者是2笔交易，这里是k笔交易，只不过状态数目需要根据k的大小进行确定而已。根据前者的递推公式可以得到这道题递推公式的规律。另外需要特别注意在买入股票这个操作下有两个特殊情况，即有无起始金额，遇到无起始金额的情况需要额外进行递推。
Code
class Solution(object):def maxProfit(self, k, prices):""":type k: int:type prices: List[int]:rtype: int"""# k笔，2k个状态# 1. dp数组定义，dp[i][2k]dp = [ [float('-inf')] * 2*k for _ in range(len(prices))]# 2. dp初始化# 偶数购入，奇数卖出# dp[0][0] = -pirces[0]# dp[0][1] = 0# dp[0][2] = -pirces[0]# dp[0][3] = 0for i in range(2*k):if i%2 == 0:dp[0][i] = -prices[0]elif i%2 == 1:dp[0][i] = 0# print(dp)# 3. 递推公式# dp[i][0] = max(dp[i-1][0], -pirces[i]+dp[i-1][1])# dp[i][1] = max(dp[i-1][0], pirces[i]+dp[i-1][0])# 4. 遍历顺序for i in range(1, len(prices)):for j in range(2*k):if j == 0: ### 这是特殊情况，买入的情况分为两种，有起始金额和没起始金额 dp[i][j] = max(dp[i-1][j], -prices[i])elif j % 2 == 0:dp[i][j] = max(dp[i-1][j], -prices[i]+dp[i-1][j-1])elif j % 2 == 1:dp[i][j] = max(dp[i-1][j], prices[i]+dp[i-1][j-1])# 5. dp数组打印# print(dp)return dp[-1][2*k-1]LeetCode 309.最佳买卖股票时机含冷冻期
手撕Code
class Solution(object):def maxProfit(self, prices):""":type prices: List[int]:rtype: int"""# 可以多次购买一只股票，不限制次数，因此两个状态可以衡量# 1. dp数组定义dp = [ [float('-inf')] * 2 for _ in range(len(prices)) ]# 2. dp数组初始化dp[0][0] = -prices[0]dp[0][1] = 0# 3. dp递推公式# dp[i][0] = max(dp[i-1][0], dp[i-2][1]-prices[i]) ## 没有冷静期时的递推公式# dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i])# 4. 遍历顺序for i in range(1, len(prices)):if i < 2: ## 前两天进行买入卖出无所谓，关键在于卖出后的冷静期。dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])else:dp[i][0] = max(dp[i-1][0], dp[i-2][1]-prices[i]) ## 买入时的股票一定是在前天之前交易完后才能买入（中间隔了一天冷静期）dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]) # 5. dp打印# print(dp)return dp[-1][1]上述代码可以在LeetCode上通过，dp[i][0] = dp[i-2][1]-prices[i]可以很好地限定后续买入股票一定是基于前天卖出股票后才进行的。但可能是刚好由于冷冻期是一天，因此if i < 2可以解决这种做法存在的缺陷，当冷冻期长时，这种做法可能就行不通了（需要检验一下）。由于卖出+冷冻期+买入一共是三天，因此起始时说不会有冷冻期这种说法的，因此要if i < 2来限定让前两天能够取到最大利润。
将各状态进行区分设计dp数组的做法
思路：
由于本道题有三个状态，买入-卖出-冷冻期；又由于冷冻期与具体哪一天卖出股票（之前卖出股票状态是表示第i天之前（包括第i天）的状态，现在是切分成了第i天前的股票状态，和第i天进行股票卖出的操作）相关，因此本道题涉及到冷冻期买卖股票的有四种状态，第i天前(包括第i天)股票，第i天前卖出股票，具体第i天卖出股票，第i天是冷冻期。因此，dp数组定义如下：
1. dp数组定义
- dp[i][0]: 第i天前(包括第i天)买入股票
- dp[i][1]: 第i天前卖出股票的状态
- dp[i][2]: 具体第i天卖出股票
- dp[i][3]: 第i天是冷冻期
2. 递推公式
dp[i][0] = max(dp[i-1][0], dp[i-1][3]-prices[i], dp[i-1][1]-prices[i])
- dp[i][0] = dp[i-1][0], 表示第i天没买入股票，延续之前买入股票的状态。
- dp[i][0] = dp[i-1][3]-prices[i]，表示买入股票，且昨天是冷冻期。
- dp[i][0] = dp[i-1][1]-prices[i]，表示买入股票，且基于之前所获得的起始金额。
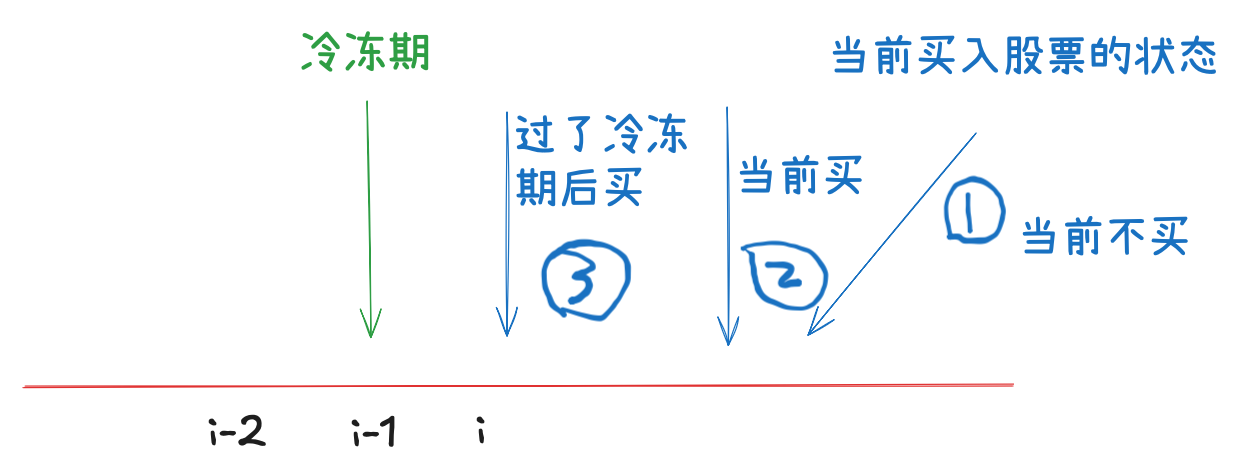
dp[i][1] = max(dp[i-1][1], dp[i-1][2])
- dp[i][1] = dp[i-1][1], 表示之前卖出股票，且已经过了冷冻期，故继承之前卖出股票的状态。
- dp[i][1] = dp[i-1][2], 表示昨天卖出股票，今天是冷冻期，故继承冷冻期前卖出股票的状态。
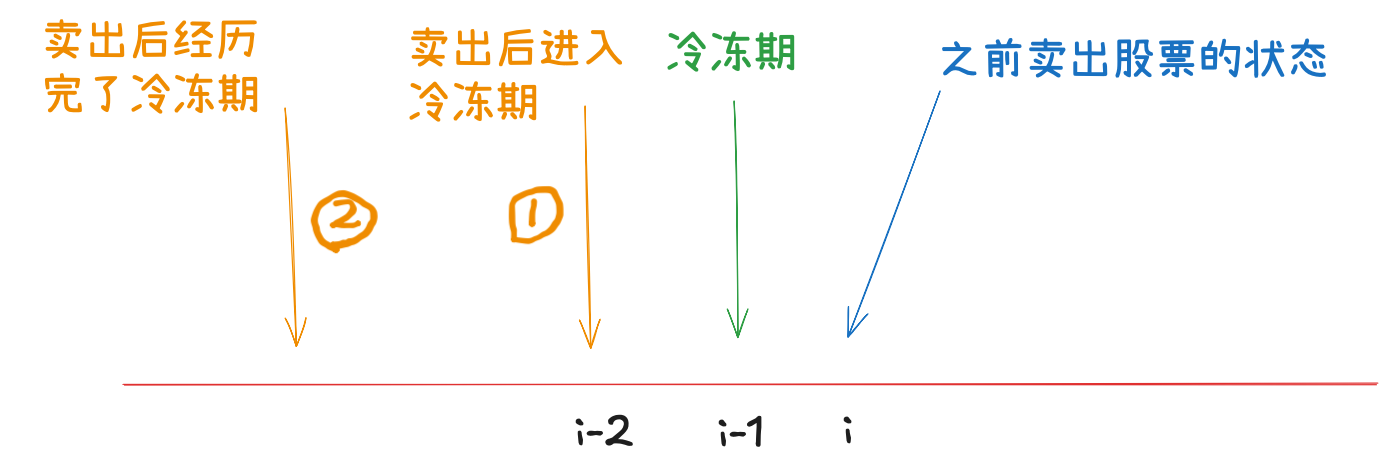dp[i][2] = dp[i-1][0] + prices[i]
- dp[i][2] = dp[i-1][0] + prices[i]，表示第i天卖出股票
dp[i][3]= dp[i-1][2]
- dp[i][3]= dp[i-1][2]，第i天的冷静期状态，取决于i-1天是否卖出股票。
Code
class Solution(object):def maxProfit(self, prices):""":type prices: List[int]:rtype: int"""## 1. dp数组定义# dp[i][0] 第i天前(包括第i天)买入股票的状态# dp[i][1] 第i天前卖出股票的状态# dp[i][2] 第i天卖出股票的状态# dp[i][3] 第i天冷静期时的状态dp = [[float('-inf')]*4 for _ in range(len(prices))]## 2. 递推公式## 3. 初始化## 4. 遍历顺序dp[0][0] = -prices[0]dp[0][1] = 0dp[0][2] = 0dp[0][3] = 0for i in range(1,len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i], dp[i-1][3]-prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][3])dp[i][2] = dp[i-1][0] + prices[i]dp[i][3] = dp[i-1][2]# 5. 打印dp# print(dp)return max(dp[-1][1], dp[-1][2], dp[-1][3])LeetCode 714.买卖股票的最佳时机含手续费
思路：
跟多次买卖股票得到最大利润的类似，只不过需要减去手续费。
另外，需要特别注意当第一天的卖出股票状态不能为负，最小为0，不然的话会默认成了起始金额是负值，导致向右递推出现错误。
class Solution(object):def maxProfit(self, prices, fee):""":type prices: List[int]:type fee: int:rtype: int"""# 1. dp数组定义dp = [[float('-inf')]*2 for _ in range(len(prices))]# 2. dp初始化dp[0][0] = - prices[0]dp[0][1] = 0 ### 需要注意的是，若是第一天利润已经小于0了，那就初始化为0，此时需要默认不对股票进行操作。否则，起始金额在向右进行递推的时候会出现错误。# 3.递推公式# dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])# dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)# 4. 遍历顺序for i in range(1, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)# 5. 打印dp# print(dp)return dp[-1][1]