当前位置：首页 > news >正文

位置编码(position embedding)

news 2025/7/25 9:38:53

点乘与旋转变化

在直角坐标系中，对于向量 $x\mathbf{x}$ 和 $y\mathbf{y}$ 来说，其点乘满足公式 $xT⋅y=∣∣x∣∣⋅∣∣y∣∣⋅cosγ\mathbf{x^T} \cdot \mathbf{y}=||x||\cdot||y||\cdot cos\gamma$ 。这个夹角就是两个向量之间的相对向量。只要两个向量的模长不变，夹角不变，无论在坐标系的哪个位置，点乘的结果就不会发生变化。
在线性代数中，矩阵是可以表示线性变换的。对于二位向量 $x\mathbf{x}$ ，绕原点旋转 $m$ 弧度后，变成 $Rm⋅xR_m\cdot \mathbf{x}$ 。其中，矩阵 $R_m$ 的形式如下：
$R_m= \begin{bmatrix} cosm & -sinm \\ sinm & cosm \end{bmatrix}$
进一步可得到 $RmT⋅Rn=Rn−mR_m^T\cdot R_n=R_{n-m}$ 。其中， $n - m$ 就可以理解为旋转弧度的相对信息。

为什么需要位置编码？

在Transformer出现以前，NLP任务大多是以RNN，LSTM为代表的循环处理方式：一个token一个token的输入到当前模型中。虽然这样使得模型天生就包含了token在序列中的位置信息。但是也有很多缺陷：
1.会出现"遗忘"现象，随着模型的进行，前面的信息出遗忘。
2.有时候句子越靠后的token对结果的影响越大。
3.只能利用上文信息，不能获取下文信息。
4.循环网络是一个token一个token输入的，只能串行计算，计算时间复杂度较高。
Transformer出现后，能同时获取上下文信息、遗忘的问题也解决了。但是模型没有办法知道每个token在句子中的相对和绝对位置信息。

在Transformer的输入层中，使用了Positional Encodeing，最终的输入表示为Input = embedding+positional_encoding。

为什么这里是加法？
我个人比较赞成其中一个说法：
假设每一个位置的token向量表示为 $xi∈R(d,1)x^i \in R^{(d,1)}$ ，给其concat一个代表位置信息的one-hot向量 $pi∈R(N,1)p^i \in R^{(N,1)}$ ，（N代表有N个位置）形成 $xpi∈R(d+N,1)=[xipi]x_p^i \in R^{(d+N,1)}=\begin{bmatrix} x^i \\ p^i \end{bmatrix}$ 。
然后对其做线性变换，映射到我们需要的维度 $d$ ，记变换矩阵 $W∈R(d,d+N)=[WI,Wp]，Wi∈R(d,d),Wp∈R(d,N)W\in R^{(d,d+N)}=\begin{bmatrix} W^I , W^p \end{bmatrix}，W^i \in R^{(d,d)},W^p \in R^{(d,N)}$ 。
变换结果：
$W⋅xpi=[WI,Wp]⋅[xipi]=WI⋅xi+Wp⋅xp=emdedi+posiW\cdot x_p^i=\begin{bmatrix} W^I , W^p \end{bmatrix}\cdot \begin{bmatrix} x^i \\ p^i \end{bmatrix}=W^I\cdot x^i +W^p \cdot x^p=emded^i+pos^i$
由变换结果可知，在原始输入上concat一个位置向量在经过线性变换后等同于将输入经过线性变换后直接加上位置编码。

Position Encoding

位置编码的公式如下：
$PE_t^{(i)} = \begin{cases} \sin(w_k t), & \text{if } i = 2k \\ \cos(w_k t), & \text{if } i = 2k + 1 \end{cases}$
$wk=1100002idw_k=\frac{1}{10000^{\frac{2i}{d}}}$
对于 $s in (w * p os)$ 函数， $w$ 越小，周期越大，频率越小，震荡就越慢。
1.为什么要这样设计 $w_k$ ？
显然，维度 $i$ 越小， $w_i$ 越大—>表示周期短，频率高。
这样对于两个相邻位置pos=1和pos=2.
用高频的函数，比如sin(1pos):
$sin(1∗1)≈0.84sin(1*1)\approx 0.84$
$sin(1∗2)≈0.91sin(1*2)\approx 0.91$
用低频正弦函数，比如sin(0.0001pos):
$sin(0.0001∗1)≈0.0001sin(0.0001*1)\approx 0.0001$
$sin(0.0001∗2)≈0.0002sin(0.0001*2)\approx 0.0002$
对于相邻位置，变化极小，难以区分。
所以高频位置编码在相邻位置之间的值变化很大，模型容易感知到“位置的微小差异”。

2.既然高频位置编码高频率能感受到微小的位置信息差异，为什么在维度增加时反而让频率变小？
前面已经提到高频变化能清晰捕捉到局部的相对位置变化。
但对于长距离的位置变化，由于sin函数周期重叠的原因，无法建立长期依赖。
比如说： $s in (1000 t)$ 在 $t = 0 和 t = 10$ 内已经震荡很多次了。
⁡因此：低维捕捉细节，高维捕捉全局。
3.为什么又添加了cos交替来表示位置？
目前为止只使用 $s in$ 的位置向量实现了如下功能：
1）每个token的向量唯一
2）位置向量的值是有界的，且位于连续空间中，模型更容易泛化。

但是这样只能表示一个token的绝对位置，还需想个办法表示相对位置。即需要满足： $PEt+△t=T△t∗PEtPE_{t+\bigtriangleup t}=T_{\bigtriangleup t}*PE_t$
那么我们就可以把 $T△tT_{\bigtriangleup t}$ 当作一个旋转矩阵。
则上式可进一步写成：
$\begin{bmatrix} sin(t+\bigtriangleup t) \\ cos(t+\bigtriangleup t) \end{bmatrix} = \begin{bmatrix} cos\bigtriangleup t & -sin\bigtriangleup t \\ sin\bigtriangleup t & cos\bigtriangleup t \end{bmatrix} \cdot \begin{bmatrix} sin(t) \\ cos(t) \end{bmatrix}$
有了这个性质，我们就可以把原来全是sin函数的 $PE_t$ 做一个替换，让位置两两一组，分别用sin、cos来表示。就得到最终的位置编码了。

Transformer位置编码可视化

下图是一串序列长度为50，位置编码维度为128的位置编码可视化结果：
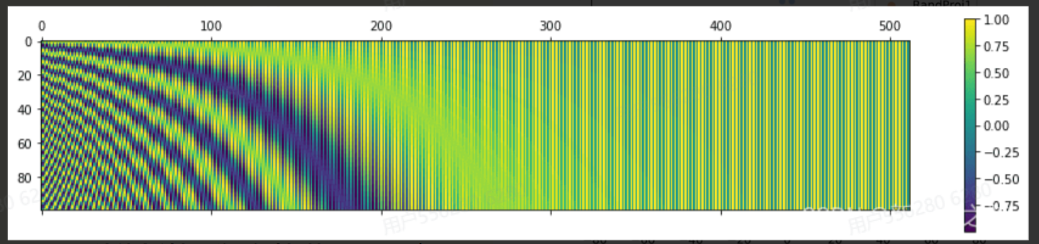
在这里插入图片描述

可以发现，由于sin/cos函数的性质，位置向量的每一个值都位于[-1, 1]之间。同时，纵向来看，图的右半边几乎都是蓝色的，这是因为越往后的位置，频率越小，波长越长，所以不同的t对最终的结果影响不大。而越往左边走，颜色交替的频率越频繁。

重要性质

性质1）：两个位置编码的点积仅取决于位置偏移量，也即两个位置编码的点积可以反映出两个位置编码的距离。
证明：
以二维向量为例，可扩展至多维场景。
$\begin{aligned} PE_t * PE_{t+\bigtriangleup t} &=[sin(w_it) ,cos(w_it)]\cdot [sin(w_i({t+\bigtriangleup t})，cos(w_i({t+\bigtriangleup t}))]^T \\ &=cos(w_i{t+\bigtriangleup t}) \end{aligned}$
性质2）：位置编码的点积是无向的，即 $PEtT⋅PEt+△t=PEtT⋅PEt−△tPE_t^T\cdot PE_{t+\bigtriangleup t}=PE_t^T\cdot PE_{t-\bigtriangleup t}$
也就是说，虽然位置向量的点积可以用于表示距离(distance-aware)，但是它却不能用来表示位置的方向性(lack-of-directionality)。

缺点

进入attention层后，内积的距离意识模式也遭到了破坏。尽管Transformer的原始位置编码能够间接地表示相对位置信息，但这种表示并不是直接或显式的。

$x_i=embed_i+PE_i$
$Q=xW_Q,K=xW_k$
利用 $attention_score=softmax(Qi⋅Kj)attention\_score=softmax(Q_i\cdot K_j)$ 来判断i和j两个token的之间的相关性。
但是显然，位置编码虽然加入了位置信息，但是在经过一系列线性变换后，原来我们可以直接感受到的“哪个token离我仅，哪个远”的位置感知能力被破坏了。
attention分数完全依赖 $Q 和 K$ 的点积，而不是 $∣ i - j ∣$
位置信息变成隐含因素，模型不能直接感知“相对距离”。
总的来说就是加法注入的方式太“弱”，不能在深层保持。