数字化转型：概念性名词浅谈（第三十四讲）

大家好，今天接着介绍数字化转型的概念性名词系列。

（1）线性规划问题

线性规划问题又称线性规划，在数学中线性规划（Linear Programming，简称LP）特指目标函数和约束条件皆为线性的最优化问题。

线性规划是最优化问题中的一个重要领域。在作业研究中所面临的许多实际问题都可以用线性规划来处理，特别是某些特殊情况，例如：网络流、多商品流量等问题，都被认为非常重要。现阶段已有大量针对线性规划算法的研究。很多最优化问题算法都可以分解为线性规划子问题，然后逐一求解。在线性规划的历史发展过程中所衍伸出的诸多概念，建立了最优化理论的核心思维，例如“对偶”、“分解”、“凸集”的重要性及其一般化等。在微观经济学和商业管理领域中，线性规划亦被大量应用于例如降低生产过程的成本等手段，最终提升产值与营收。乔治·丹齐格被认为是线性规划之父。

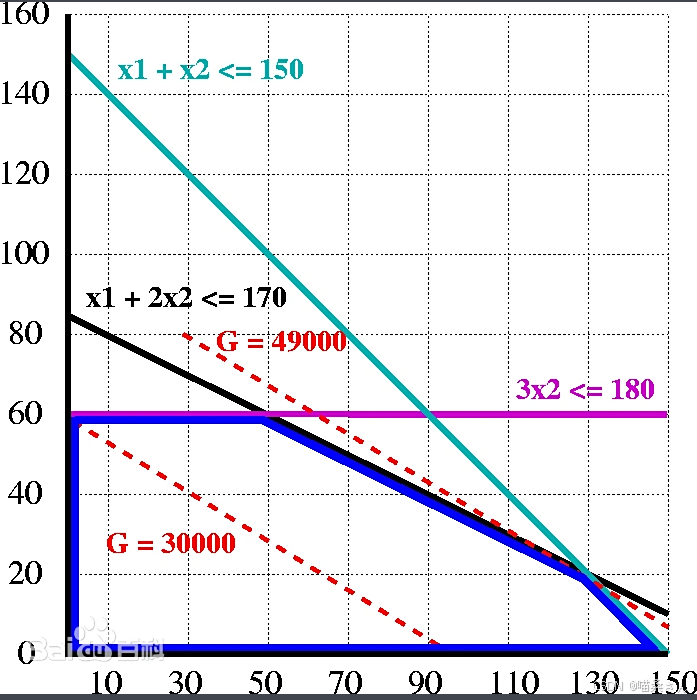
几何上，线性约束条件的集合相当于一个凸包或凸集，叫做可行域。因为目标函数亦是线性的，所以其极值点会自动成为最值点。线性目标函数亦暗示其最优解只会在其可行域的边界点中出现。

在两种情况下线性规划问题没有最优解。其中一种是在约束条件相互矛盾的情况下，其可行域将会变成空集，问题没有解，因此亦没有最优解。在这种情况下，该线性规划问题会被称之为“不可行”。

另一种情况是，约束条件的多面体可以在目标函数的方向无界，目标函数可以取得任意大的数值，所以没有最优解。

除了以上两种病态的情况以外（问题通常都会受到资源的限制，如上面的例子），最优解永远都能够在多面体的顶点中取得。但最优解未必只有一个：有可能出现一组最优解，覆盖多面体的一条边、一个面、甚至是整个多面体（最后一种情况会在目标函数只能等于0的情况下出现）。

要求所有的未知量都为整数的线性规划问题叫做整数规划（integer programming, IP）或整数线性规划（integer linear programming, ILP）问题。相对于即使在最坏情况下也能有效率地解出的线性规划问题，整数规划问题的最坏情况是不确定的，在某些实际情况中（有约束变量的那些）为NP困难问题。

0-1整数规划是整数规划的特殊情况，所有的变量都要是0或1（而非任意整数）。这类问题亦被分类为NP困难问题 [2]。

只要求当中某几个未知数为整数的线性规划问题叫做混合整数规划（mixed integer programming, MIP）问题。这类问题通常亦被分类为NP困难问题。

存在着几类IP和MIP的子问题，它们可以被有效率地解出，最值得注意的一类是具有完全单位模约束矩阵，和约束条件的右边全为整数的一类。

一个解决大型整数线性规划问题的先进算法为delayed column generation。

（2）动态规划

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。

动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法比用其它方法求解更为方便 。

虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时间无关的静态规划(如线性规划、非线性规划)，只要人为地引进时间因素，把它视为多阶段决策过程，也可以用动态规划方法方便地求解 。

概念引入

在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线。这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法。

基本思想

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式 。

本篇文章要介绍的就是这么多，我们下篇文章再见。