当前位置：首页 > news >正文

深度相机---像素转物理尺寸

news 2025/7/25 11:25:19

深度相机（如TOF相机、结构光相机、双目立体相机）的核心价值在于能同时输出二维图像和三维深度信息，而将图像中的像素尺寸转换为真实物理尺寸（如米、毫米）是其在工业测量、机器人导航、三维重建等领域的关键应用。这一转换过程涉及光学原理、坐标系转换、相机校准等多方面知识，需结合深度信息、相机内参、视场角等参数，通过几何关系推导实现。

一、核心概念与坐标系基础

在进行像素到物理尺寸的转换前，需明确四个核心坐标系及它们之间的映射关系。

1. 四个关键坐标系

像素坐标系（u, v）：图像中像素的位置，以左上角为原点（0,0），横向为u轴（像素列），纵向为v轴（像素行），单位为“像素”。例如，640×480分辨率的图像中，像素坐标范围为u∈[0,639]，v∈[0,479]。
图像坐标系（x, y）：以像素物理尺寸为单位的二维坐标系，原点为图像光学中心（主点），x轴与u轴平行，y轴与v轴平行，单位为“米”（或毫米）。其与像素坐标系的关系为： $x=(u-u_0)p_x$ ， $y=(v-v_0)p_y$ ，其中 $u_0,v_0$ 为主点的像素坐标（光学中心在图像中的像素位置）， $p_x,p_y$ 为单个像素的物理宽高（如 $p_x=3μm$ 表示1像素的物理宽度为3微米）。
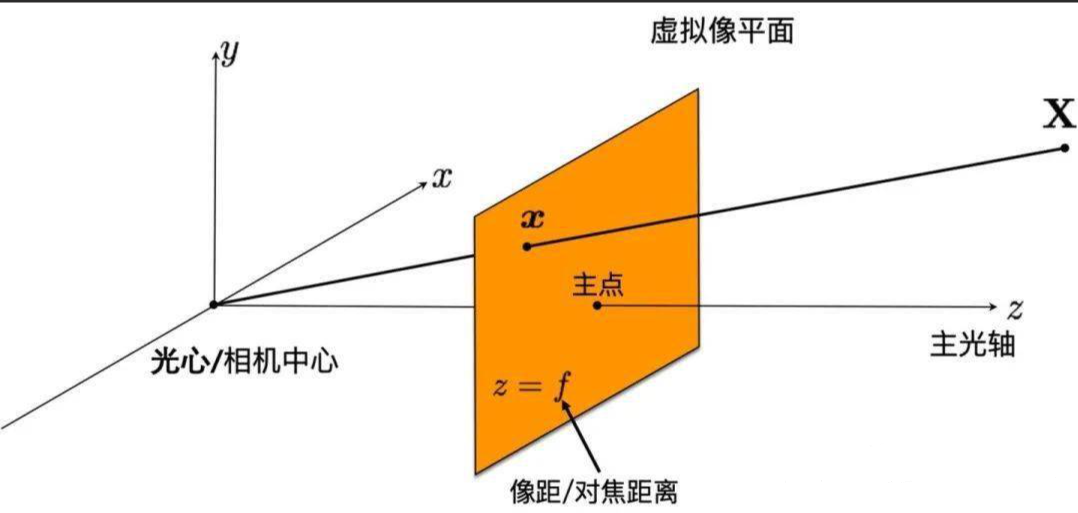
相机坐标系（X, Y, Z）：以相机光心为原点的三维坐标系，Z轴为光轴方向（垂直于像平面），X轴与图像坐标系x轴平行，Y轴与y轴平行，单位为“米”。该坐标系是连接二维图像与三维物理空间的桥梁。
世界坐标系（X_w, Y_w, Z_w）：自定义的三维参考坐标系（如地面坐标系、物体自身坐标系），需通过相机外参（旋转矩阵 $R$ 、平移向量 $T$ ）与相机坐标系关联。

2. 深度信息的本质

深度相机输出的“深度图”中，每个像素（u, v）对应的深度值 $Z$ ，本质是该点在相机坐标系中的Z坐标（即该点到光心的距离，单位通常为米或毫米）。

二、转换的核心原理：从像素坐标到物理尺寸

像素尺寸到物理尺寸的转换，本质是通过相机的光学参数（内参、视场角）和深度信息，建立“像素差”与“物理距离”的映射关系。其核心逻辑可概括为：先将像素坐标转换为相机坐标系下的三维坐标，再通过坐标系关系得到物理尺寸。

1. 相机内参：

相机内参矩阵（Intrinsic Matrix）是描述相机光学特性的关键参数，通过相机校准（如张正友标定法）获得，其表达式为：
$\begin{bmatrix} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix}$
其中：

$f_x = f / p_x$ 、 $f_y = f / p_y$ ：像素焦距（单位：像素）， $f$ 为镜头物理焦距（单位：米）， $p_x、p_y$ 为单个像素的物理宽高（单位：米/像素）；
$u_0、v_0$ ：主点（光学中心）的像素坐标（通常接近图像中心，但受镜头装配影响可能偏移）。

2. 像素坐标到相机坐标系的转换

对于图像中任意像素（u, v），其在相机坐标系中的三维坐标（X, Y, Z）可通过内参矩阵推导：

先将像素坐标（u, v）转换为图像坐标系坐标（x, y）：
$u_0) \cdot p_x, \quad y = (v - v_0) \cdot p_y$
结合深度 $Z$ （相机坐标系Z坐标），根据相似三角形原理（光心、像素点、三维空间点构成相似三角形），推导相机坐标系的X、Y坐标：
$X=Z⋅xf=Z⋅(u−u0)⋅pxf=Z⋅u−u0fx\frac{X}{Z} = \frac{x}{f} \implies X = Z \cdot \frac{x}{f} = Z \cdot \frac{(u - u_0) \cdot p_x}{f} = Z \cdot \frac{u - u_0}{f_x}$
同理：
$\cdot \frac{v - v_0}{f_y}$

最终，像素（u, v）在相机坐标系中的三维坐标为：
$\left( Z \cdot \frac{u - u_0}{f_x}, \quad Z \cdot \frac{v - v_0}{f_y}, \quad Z \right)$

在这里插入图片描述

3. 物理尺寸的计算：基于两点坐标差

若需计算图像中两个点（ $u_1, v_1$ ）和（ $u_2, v_2$ ）之间的物理距离，可通过以下步骤：

分别获取两点的深度值 $Z_1、Z_2$ （若两点在同一平面且与相机平行，可近似取 $Z_1=Z_2=Z$ ）；
计算两点在相机坐标系中的三维坐标：
$(X1,Y1,Z1)=(Z1⋅u1−u0fx,Z1⋅v1−v0fy,Z1)(X_1, Y_1, Z_1) = \left( Z_1 \cdot \frac{u_1 - u_0}{f_x}, \quad Z_1 \cdot \frac{v_1 - v_0}{f_y}, \quad Z_1 \right)$
$(X2,Y2,Z2)=(Z2⋅u2−u0fx,Z2⋅v2−v0fy,Z2)(X_2, Y_2, Z_2) = \left( Z_2 \cdot \frac{u_2 - u_0}{f_x}, \quad Z_2 \cdot \frac{v_2 - v_0}{f_y}, \quad Z_2 \right)$
两点间的物理距离（三维欧氏距离）为：
$\sqrt{(X_2 - X_1)^2 + (Y_2 - Y_1)^2 + (Z_2 - Z_1)^2}$

若两点在同一深度平面（ $Z_1=Z_2=Z$ ），则简化为二维距离：
$\sqrt{\left( Z \cdot \frac{u_2 - u_1}{f_x} \right)^2 + \left( Z \cdot \frac{v_2 - v_1}{f_y} \right)^2}$

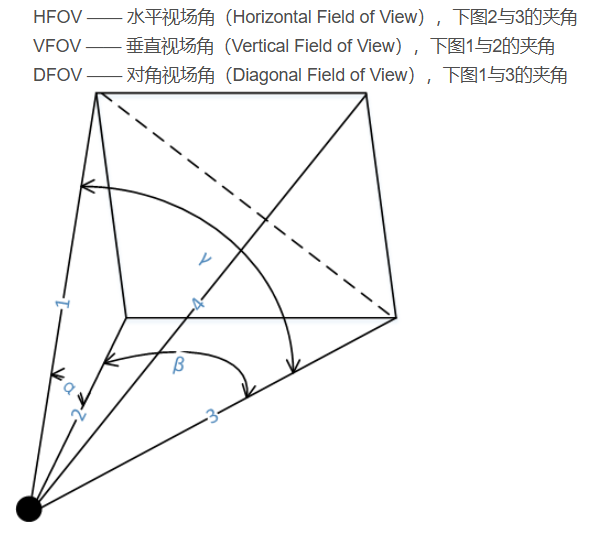
视场角（FOV)

1. 基础定义

视场角（FOV）：相机能够捕捉到的视野范围，通常分为水平视场角（θₕ） 和垂直视场角（θᵥ），单位为角度（°）或弧度（rad）。例如，水平视场角60°表示相机在水平方向能覆盖从光轴向左30°到向右30°的范围。
像素（Pixel）：图像的最小离散单位，通常用图像的水平像素数（W，如1920） 和垂直像素数（H，如1080） 描述图像尺寸（如1920×1080）。

2. 核心关系：角度分辨率

视场角和像素的直接关系体现为**“每个像素对应的角度”（即角度分辨率**），它描述了“图像中1个像素的变化对应实际场景中多大的角度范围”。

公式：像素对应的角度分辨率

对于水平方向：
$水平角度分辨率=水平视场角（θh）水平像素数（W）\text{水平角度分辨率} = \frac{\text{水平视场角}（θₕ）}{\text{水平像素数}（W）}$
（单位：度/像素或弧度/像素）

对于垂直方向：
$垂直角度分辨率=垂直视场角（θv）垂直像素数（H）\text{垂直角度分辨率} = \frac{\text{垂直视场角}（θᵥ）}{\text{垂直像素数}（H）}$

3. 物理意义：从角度到空间尺度的转换

角度分辨率仅描述了像素与角度的对应关系，若结合相机到目标的距离（depth），可进一步将“像素”转换为“实际物理尺寸”（如米、厘米），这也是视场角与像素在实际应用中的核心价值。

以水平方向为例：

已知水平视场角θₕ，相机到目标的距离为depth，则相机在水平方向能覆盖的实际物理宽度（Lₕ） 为：
$\cdot depth \cdot \tan\left(\frac{θₕ}{2}\right)$
（原理：视场角对称分布在光轴两侧，通过三角函数将角度转换为线性距离）
图像水平像素数为W，则每个水平像素对应的实际物理长度（ΔLₕ） 为：
$\frac{Lₕ}{W} = \frac{2 \cdot depth \cdot \tan\left(\frac{θₕ}{2}\right)}{W}$

在这里插入图片描述
下面是通过视场角算出像素图对应实际物理尺寸Ground Pixel Area的C++代码

double GPA(double depth, int img_view_rows, int img_view_cols)
{double length = depth * tan(theta_length) * 2 / img_view_cols;double width = depth * tan(theta_width) * 2 / img_view_rows;return length * width;
}

4. 视场角（FOV）与内参的关联：无内参时的替代方案

若未获取相机内参，可通过视场角（FOV）推导转换关系。视场角是相机可观测的角度范围（水平HFOV、垂直VFOV），与内参的关系为：
$tan⁡(HFOV2)=(W/2−u0)⋅pxf=W/2−u0fx(假设主点在中心，u0=W/2)\tan\left( \frac{HFOV}{2} \right) = \frac{(W/2 - u_0) \cdot p_x}{f} = \frac{W/2 - u_0}{f_x} \quad (\text{假设主点在中心，}u_0=W/2)$
简化得（主点居中时）：
$fx=W/2tan⁡(HFOV/2),fy=H/2tan⁡(VFOV/2)f_x = \frac{W/2}{\tan(HFOV/2)}, \quad f_y = \frac{H/2}{\tan(VFOV/2)}$

将其代入物理尺寸公式，可得基于FOV的转换公式：

水平方向1像素对应的物理尺寸（当深度为Z时）：
$px_phys=X2−X1u2−u1=Zfx=2Z⋅tan⁡(HFOV/2)Wp_{x\_phys} = \frac{X_2 - X_1}{u_2 - u_1} = \frac{Z}{f_x} = \frac{2Z \cdot \tan(HFOV/2)}{W}$
垂直方向1像素对应的物理尺寸：
$py_phys=2Z⋅tan⁡(VFOV/2)Hp_{y\_phys} = \frac{2Z \cdot \tan(VFOV/2)}{H}$

因此，若目标在图像中占据 $Δu=∣u2−u1∣\Delta u = |u_2 - u_1|$ 像素（水平）和 $Δv=∣v2−v1∣\Delta v = |v_2 - v_1|$ 像素（垂直），其物理尺寸为：
$物理宽度=Δu⋅px_phys=Δu⋅2Z⋅tan⁡(HFOV/2)W\text{物理宽度} = \Delta u \cdot p_{x\_phys} = \Delta u \cdot \frac{2Z \cdot \tan(HFOV/2)}{W}$
$物理高度=Δv⋅py_phys=Δv⋅2Z⋅tan⁡(VFOV/2)H\text{物理高度} = \Delta v \cdot p_{y\_phys} = \Delta v \cdot \frac{2Z \cdot \tan(VFOV/2)}{H}$

三、关键细节：影响转换精度的核心因素

实际应用中，转换精度受多种因素影响，需针对性处理以避免误差累积。

1. 畸变校正：消除镜头“失真”

相机镜头存在光学畸变（径向畸变、切向畸变），导致像素坐标与理想位置偏移，若不校正会直接影响转换精度。

径向畸变：由镜头曲率导致，表现为“桶形畸变”（边缘像素向外偏移）或“枕形畸变”（边缘像素向内偏移），校正公式为：
$xcorrected=x⋅(1+k1r2+k2r4+k3r6),ycorrected=y⋅(1+k1r2+k2r4+k3r6)x_{\text{corrected}} = x \cdot (1 + k_1 r^2 + k_2 r^4 + k_3 r^6), \quad y_{\text{corrected}} = y \cdot (1 + k_1 r^2 + k_2 r^4 + k_3 r^6)$
其中 $r^2 = x^2 + y^2$ ， $k_1、k_2、k_3$ 为径向畸变系数。
切向畸变：由镜头装配偏差导致，校正公式为：
$xcorrected=x+2p1xy+p2(r2+2x2),ycorrected=y+p1(r2+2y2)+2p2xyx_{\text{corrected}} = x + 2p_1 xy + p_2 (r^2 + 2x^2), \quad y_{\text{corrected}} = y + p_1 (r^2 + 2y^2) + 2p_2 xy$
其中 $p_1、p_2$ 为切向畸变系数。

校正步骤：先通过畸变系数将像素坐标（u, v）转换为无畸变的理想坐标（ $uundistort,vundistortu_{\text{undistort}}, v_{\text{undistort}}$ ），再代入转换公式。

2. 深度信息的可靠性：精度的“基石”

深度值 $Z$ 的准确性直接决定物理尺寸精度，需注意以下问题：

深度噪声：TOF相机受多路径反射影响，结构光相机受环境光干扰，双目相机受纹理缺失影响，均会导致深度值波动（如±5%的误差）。需通过滤波（中值滤波、高斯滤波）或多帧融合降低噪声。
深度分辨率：深度图的分辨率通常低于彩色图（如1280×720彩色图对应640×360深度图），需通过像素对齐（如插值）确保像素-深度对应关系准确。
深度单位：不同相机的深度单位不同（如Intel RealSense的深度图单位为毫米，Azure Kinect为米），转换前需统一单位（如将毫米转换为米）。

3. 像素的“非正方形”特性：宽高比的影响

部分相机的像素并非正方形（如工业相机的像素宽高比为4:3），此时 $fx/fy≠W/Hf_x / f_y \neq W / H$ ，导致水平和垂直方向的1像素物理尺寸不同（ $px_phys≠py_physp_{x\_phys} \neq p_{y\_phys}$ ）。若误用正方形像素假设（ $p_x = p_y$ ），会引入2%-5%的误差。

判断方法：通过内参计算宽高比 $r = (f_x / W) / (f_y / H)$ ，若 $\neq 1$ ，则为非正方形像素，需分别计算水平和垂直方向的物理尺寸。

4. 目标平面与像平面的夹角：倾斜场景的处理

当目标平面与相机像平面不平行（如倾斜的桌面），不同像素的深度值 $Z$ 不同，此时不能用平均深度近似，需逐像素计算三维坐标后再求物理尺寸。例如：

倾斜平面上两点的深度分别为 $Z_1=1.0m$ 和 $Z_2=1.2m$ ，若直接用平均深度 $Z = 1.1 m$ 计算，可能导致5%以上的误差；
正确做法：分别用 $Z_1、Z_2$ 计算两点的（X1,Y1）和（X2,Y2），再通过三维距离公式计算物理距离。

四、实际应用：从参数获取到误差验证

1. 核心参数的获取途径

内参与畸变系数：通过相机厂商提供的校准文件（如Intel RealSense的json文件）获取；或使用OpenCV的calibrateCamera函数自行标定（需打印棋盘格，拍摄10-20张不同角度的图像）;或者用ROS2来标定。
视场角（FOV）：厂商规格书通常会标注（如HFOV=90°，VFOV=70°）；也可通过内参反推： $\cdot \arctan(W/(2f_x))$ 。
深度图：通过相机SDK获取（如realsense2库的depth_frame，k4a库的k4a_image_get_buffer）。

2. 步骤示例：测量一本书的物理尺寸

假设使用Intel RealSense D435i相机，参数如下：

分辨率：W=640像素，H=480像素；
内参： $f_x=615$ 像素， $f_y=615$ 像素， $u_0=320$ ， $v_0=240$ ；
书本在图像中的像素坐标：左上角（100, 100），右下角（500, 300），深度值 $Z = 1.0 m$ （平面与相机平行）。

计算步骤：

计算像素差： $Δu=500−100=400\Delta u = 500 - 100 = 400$ 像素， $Δv=300−100=200\Delta v = 300 - 100 = 200$ 像素；
计算物理宽度：
$宽度=Z⋅Δufx=1.0⋅400615≈0.650m=650mm\text{宽度} = Z \cdot \frac{\Delta u}{f_x} = 1.0 \cdot \frac{400}{615} \approx 0.650m = 650mm$
计算物理高度：
$高度=Z⋅Δvfy=1.0⋅200615≈0.325m=325mm\text{高度} = Z \cdot \frac{\Delta v}{f_y} = 1.0 \cdot \frac{200}{615} \approx 0.325m = 325mm$
验证：用尺子实际测量书本尺寸为645mm×320mm，误差约0.8%（在合理范围内）。

3. 误差来源与优化方案

实际转换中常见误差及解决方法：

误差来源	误差占比	优化方案
深度值误差	40%-50%	多帧平均、滤波算法、避开强反射区域
畸变未校正	15%-20%	用相机校准工具获取畸变系数并校正
内参不准确	10%-15%	重新标定（使用高精度棋盘格）
像素-深度对齐偏差	5%-10%	用相机SDK提供的对齐功能（如RealSense的align函数）
非平面目标	5%-10%	用三维点云直接计算物理尺寸