Leetcode力扣解题记录--第240题(矩阵搜索)
题目链接:240. 搜索二维矩阵 II - 力扣(LeetCode)
题目描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
-
每行的元素从左到右升序排列。
-
每列的元素从上到下升序排列。
示例 1:
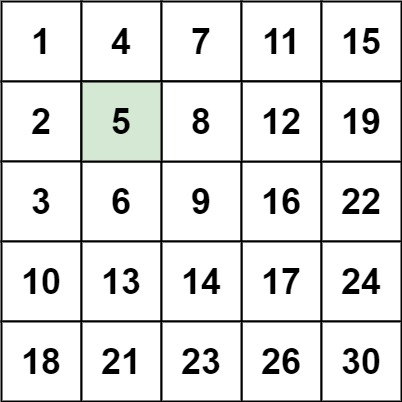
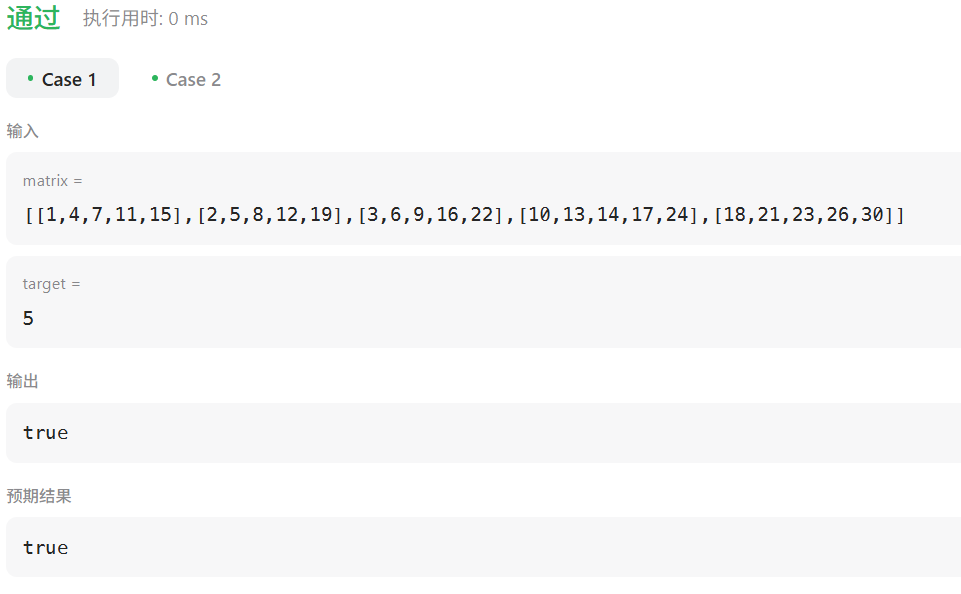
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
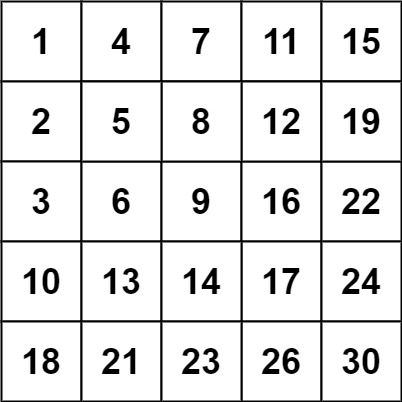
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
题目作答
解决这个问题的核心思想是利用矩阵的结构特性,逐步缩小搜索范围。一个低效的方法是逐行进行二分查找,时间复杂度为 O(m log n),但这并未完全利用“列也排序”的特性。
最高效的算法是“Z”字形或“马鞍点”查找法。该方法的巧妙之处在于选择一个合适的起点,使得每一步比较后都能明确地排除一行或一列,从而将搜索空间线性地减小。
这个理想的起点是矩阵的右上角(或者左下角也可以)。为什么是右上角呢?
-
选择起点:我们将搜索指针初始化在矩阵的右上角,即 (row = 0, col = n - 1)。
-
比较与移动:
-
令当前元素为 current = matrix[row][col]。
-
如果 current == target:恭喜,我们找到了目标值,直接返回 true。
-
如果 current > target:因为当前行的元素从左到右是递增的,所以 target 不可能在 current 的右边。同时,因为当前列的元素从上到下是递增的,所以 target 也不可能在 current 的下方(下方的元素都比current大)。因此,唯一可能的位置是在 current 的左边。我们可以安全地排除当前所在的整列,将指针向左移动一位,即 col--。
-
如果 current < target:因为当前列的元素从上到下是递增的,所以 target 不可能在 current 的上方。同时,因为当前行的元素从左到右是递增的,所以 target 也不可能在 current 的左边(左边的元素都比current小)。因此,唯一可能的位置是在 current 的下方。我们可以安全地排除当前所在的整行,将指针向下移动一位,即 row++。
-
-
终止条件:我们重复上述比较和移动的过程,直到找到 target,或者指针移出了矩阵的边界(row 超出下边界或 col 超出左边界)。如果循环结束仍未找到,说明矩阵中不存在该目标值。
这个算法在每一步都稳定地排除一行或一列,其路径最多走 m + n 步,因此时间复杂度为 O(m + n),空间复杂度为 O(1),非常高效。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {// 处理边界情况if (matrix.empty() || matrix[0].empty()) {return false;}int m = matrix.size();int n = matrix[0].size();// 1. 从矩阵的右上角开始搜索int row = 0;int col = n - 1;// 循环条件:指针在矩阵边界内while (row < m && col >= 0) {int current = matrix[row][col];if (current == target) {// 2. 找到了目标值return true;} else if (current > target) {// 3. 当前值大于目标值,排除当前列,向左移动col--;} else { // current < target// 4. 当前值小于目标值,排除当前行,向下移动row++;}}// 如果循环结束仍未找到,说明目标值不存在return false;}
};