深度学习 --- 激活函数
深度学习 — 激活函数
文章目录
- 深度学习 --- 激活函数
- 一,基础概念
- 1.1 线性
- 1.2 非线性可视化
- 1.3总结
- 二,常见的激活函数
- 2.1 sigmoid
- 2.2 tanh
- 2.3 Relu
- 2.4 LeakyRelu
- 2.5 softmax
一,基础概念
激活函数的作用是在隐藏层引入非线性,使得神经网络能够学习和表示复杂的函数关系,使网络具备非线性能力,增强其表达能力。
1.1 线性
- 核心观点:如果神经网络的隐藏层不使用激活函数,整个网络将表现为一个线性模型,无法捕捉数据中的非线性关系。
- 数学推导:
- 单层网络:输出为线性变换,即
对于单层网络(输入层到输出层),如果没有激活函数,输出a(1)\mathbf{a}^{(1)}a(1) 可以表示为:
a(1)=W(1)x+b(1)\mathbf{a}^{(1)} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}a(1)=W(1)x+b(1)
- 多层网络:
如果有L层,每层都没有激活函数,则第l层的输出为:a(l)=W(l)a(l−1)+b(l)\mathbf{a}^{(l)} = \mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}a(l)=W(l)a(l−1)+b(l) - 结论:
- 激活函数是引入非线性特性、使神经网络能够处理复杂问题的关键。
- 没有激活函数的多层神经网络等价于一个单层线性模型。
1.2 非线性可视化
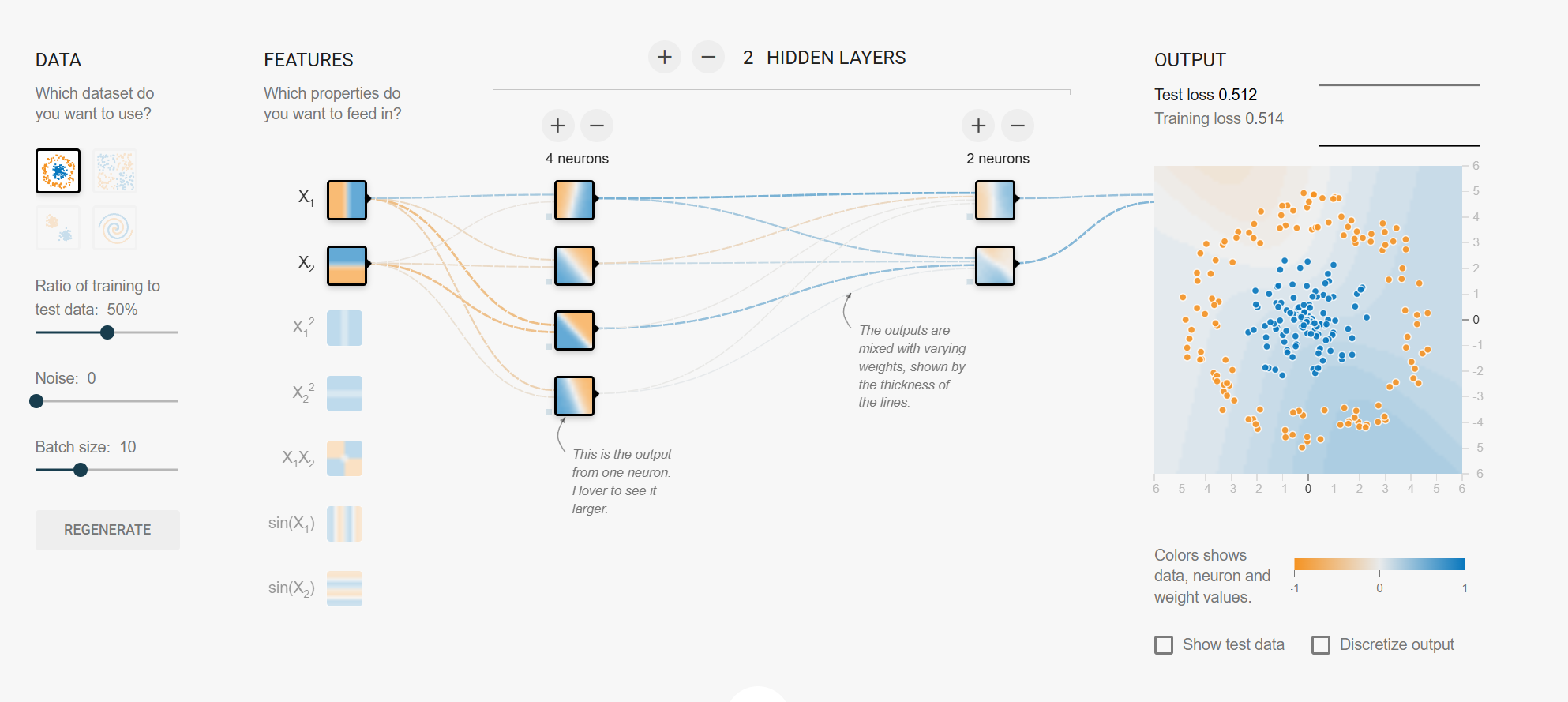
- 工具:使用 TensorFlow Playground 进行可视化。
- 可视化目的:通过可视化的方式理解非线性拟合能力。
- 可视化工具的特点:
- 可以选择不同的数据集、调整训练与测试数据的比例。
- 可以选择输入特征、调整权重和偏置。
- 可以观察神经网络的输出,通过颜色显示数据点和预测值。
- 提供了对网络结构(如隐藏层数量、激活函数等)的调整功能。
- 可视化结果:
- 激活函数的使用使得神经网络能够捕捉数据中的非线性关系。
- 不同的激活函数和网络结构对拟合能力有显著影响。
1.3总结
- 线性与非线性的重要性:
- 没有激活函数的神经网络只能处理线性问题,而现实世界中的许多问题是非线性的。
- 激活函数是神经网络能够处理复杂非线性问题的关键。
- 可视化工具的作用:
- TensorFlow Playground 提供了一个直观的方式来理解神经网络的非线性拟合能力。
- 通过调整网络结构和激活函数,可以观察到不同的拟合效果,从而更好地理解神经网络的工作原理。
二,常见的激活函数
激活函数通过引入非线性来增强神经网络的表达能力,对于解决线性模型的局限性至关重要。由于反向传播算法(BP)用于更新网络参数,因此激活函数必须是可微的,也就是说能够求导的。
2.1 sigmoid
Sigmoid激活函数是一种常见的非线性激活函数,特别是在早期神经网络中应用广泛。它将输入映射到0到1之间的值,因此非常适合处理概率问题。
| 方面 | 内容 |
|---|---|
| 公式 | f(x)=σ(x)=11+e−xf(x) = \sigma(x) = \frac{1}{1 + e^{-x}}f(x)=σ(x)=1+e−x1 |
| 特征 | 1. 将任意实数输入映射到 (0, 1) 之间,适合处理概率场景。 2. 一般用于二分类输出层。 3. 导数计算方便,可以用自身表达式表示:σ′(x)=σ(x)⋅(1−σ(x))\sigma'(x) = \sigma(x) \cdot (1 - \sigma(x))σ′(x)=σ(x)⋅(1−σ(x)) |
| 优点 | 1. 输出范围在 (0, 1) 之间,适合处理概率问题。 2. 导数计算简单,便于反向传播。 |
| 缺点 | 1. 梯度消失:输入非常大或非常小时,梯度接近于0,导致早期层权重更新缓慢,训练速度变慢甚至停滞。 2. 信息丢失:输入值相差很大时,激活值几乎相同(如输入100和10000的激活值都接近1)。 3. 计算成本高:涉及指数运算,计算复杂度比ReLU等函数高。 |
import torch
import matplotlib.pyplot as plt# plt支持中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test001():# 一行两列绘制图像_, ax = plt.subplots(1, 2)# 绘制函数图像x = torch.linspace(-10, 10, 100)y = torch.sigmoid(x)# 网格ax[0].grid(True)ax[0].set_title("sigmoid 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 在第一行第一列绘制sigmoid函数曲线图ax[0].plot(x, y)# 绘制sigmoid导数曲线图x = torch.linspace(-10, 10, 100, requires_grad=True)# y = torch.sigmoid(x) * (1 - torch.sigmoid(x))# 自动求导torch.sigmoid(x).sum().backward()ax[1].grid(True)ax[1].set_title("sigmoid 函数导数曲线图", color="red")ax[1].set_xlabel("x")ax[1].set_ylabel("y")# ax[1].plot(x.detach().numpy(), y.detach())# 用自动求导的结果绘制曲线图ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())# 设置曲线颜色ax[1].lines[0].set_color("red")plt.show()if __name__ == "__main__":test001()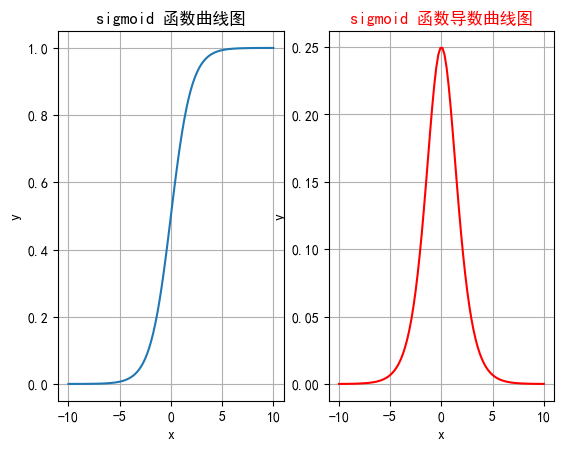
2.2 tanh
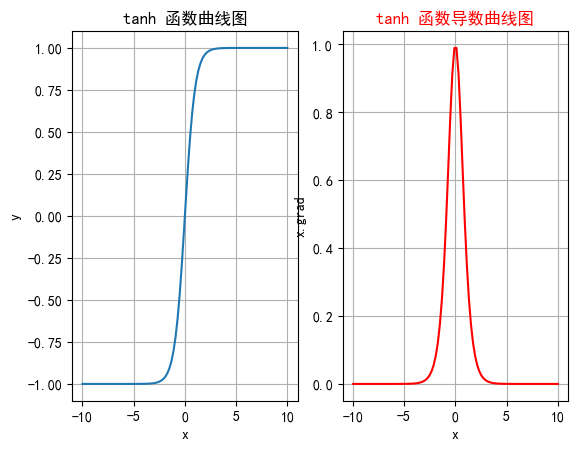
tanh(双曲正切)是一种常见的非线性激活函数,常用于神经网络的隐藏层。tanh 函数也是一种S形曲线,输出范围为(−1,1)(−1,1)(−1,1)
| 方面 | 内容 |
|---|---|
| 公式 | tanh(x)=ex−e−xex+e−x\text{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}tanh(x)=ex+e−xex−e−x |
| 特征 | 1. 输出范围在 (−1,1)(-1, 1)(−1,1) 之间,零中心化输出有助于加速收敛。 2. 是关于原点对称的奇函数,输入为0时输出也为0,有助于数据平衡。 3. 全局连续可微,导数公式为:ddxtanh(x)=1−tanh2(x)\frac{d}{dx} \text{tanh}(x) = 1 - \text{tanh}^2(x)dxdtanh(x)=1−tanh2(x)。 |
| 优点 | 1. 输出零中心化,加速收敛。 2. 对称性有助于数据平衡。 3. 全局可微,适合梯度下降优化。 |
| 缺点 | 1. 梯度消失:输入值非常大或非常小时,导数接近于0,深层网络中仍会导致训练缓慢甚至无法收敛。 2. 计算成本:涉及指数运算,计算复杂度较高,尽管与 Sigmoid 相比差异不大。 |
import torch
import matplotlib.pyplot as plt# plt支持中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test001():# 一行两列绘制图像_, ax = plt.subplots(1, 2)# 绘制函数图像x = torch.linspace(-10, 10, 100)y = torch.tanh(x)# 网格ax[0].grid(True)ax[0].set_title("tanh 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 在第一行第一列绘制tanh函数曲线图ax[0].plot(x, y)# 绘制tanh导数曲线图x = torch.linspace(-10, 10, 100, requires_grad=True)# y = torch.tanh(x) * (1 - torch.tanh(x))# 自动求导:需要标量才能反向传播torch.tanh(x).sum().backward()ax[1].grid(True)ax[1].set_title("tanh 函数导数曲线图", color="red")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")# ax[1].plot(x.detach().numpy(), y.detach())# 用自动求导的结果绘制曲线图ax[1].plot(x.detach().numpy(), x.grad.detach().numpy())# 设置曲线颜色ax[1].lines[0].set_color("red")plt.show()if __name__ == "__main__":test001()
2.3 Relu
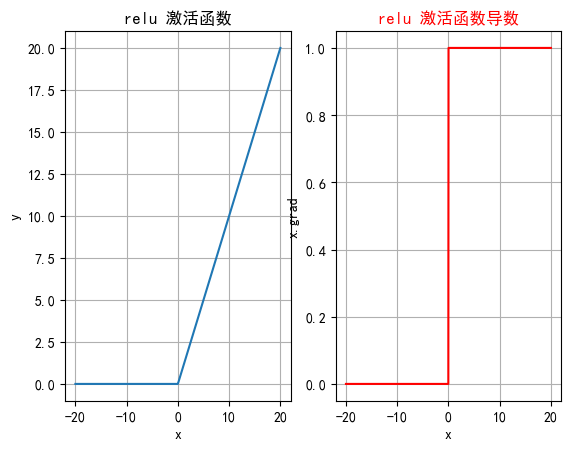
ReLU(Rectified Linear Unit)是深度学习中最常用的激活函数之一,它的全称是修正线性单元。ReLU 激活函数的定义非常简单,但在实践中效果非常好。
| 方面 | 内容 |
|---|---|
| 定义 | ReLU(x)=max(0,x)\text{ReLU}(x) = \max(0, x)ReLU(x)=max(0,x) |
| 特征 | 1. 当 x>0x > 0x>0 时,ReLU(x) = x 2. 当 x≤0x \leq 0x≤0 时,ReLU(x) = 0 3. 导数是分段函数:ReLU′(x)={1,if x>00,if x≤0\text{ReLU}'(x) = \begin{cases} 1, & \text{if } x > 0 \\ 0, & \text{if } x \leq 0 \end{cases}ReLU′(x)={1,0,if x>0if x≤0 4. 计算简单,只需要一次比较运算。 |
| 优点 | 1. 计算简单:加速神经网络的训练。 2. 缓解梯度消失问题:在正半区导数恒为1,不存在饱和问题,有利于深层网络的梯度传播。 3. 稀疏激活:引入稀疏性,减少冗余信息,提高效率和泛化能力。 |
| 缺点 | 1. 神经元死亡问题:当输入小于等于0时,神经元输出为0,且导数为0,可能导致神经元永远不再激活,降低模型的表达能力。 |
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt# 中文问题
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test006():# 输入数据xx = torch.linspace(-20, 20, 1000)y = F.relu(x)# 绘制一行2列_, ax = plt.subplots(1, 2)ax[0].plot(x.numpy(), y.numpy())# 显示坐标格子ax[0].grid()ax[0].set_title("relu 激活函数")ax[0].set_xlabel("x")ax[0].set_ylabel("y")# 绘制导数函数x = torch.linspace(-20, 20, 1000, requires_grad=True)F.relu(x).sum().backward()ax[1].plot(x.detach().numpy(), x.grad.numpy())ax[1].grid()ax[1].set_title("relu 激活函数导数", color="red")# 设置绘制线色颜色ax[1].lines[0].set_color("red")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")plt.show()if __name__ == "__main__":test006()
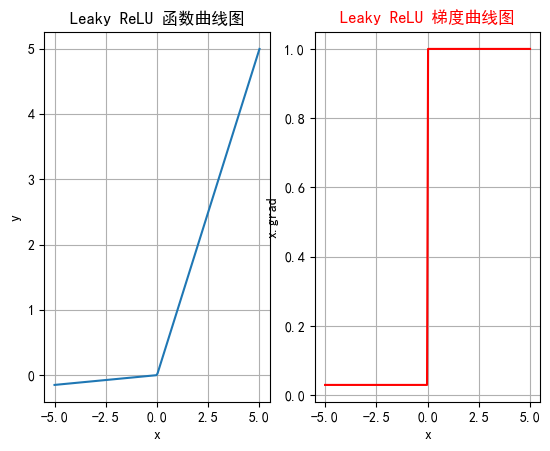
2.4 LeakyRelu
Leaky ReLU是一种对 ReLU 函数的改进,旨在解决 ReLU 的一些缺点,特别是Dying ReLU 问题。Leaky ReLU 通过在输入为负时引入一个小的负斜率来改善这一问题。
| 方面 | 内容 |
|---|---|
| 定义 | Leaky ReLU(x)={x,if x>0αx,if x≤0\text{Leaky ReLU}(x) = \begin{cases} x, & \text{if } x > 0 \\ \alpha x, & \text{if } x \leq 0 \end{cases}Leaky ReLU(x)={x,αx,if x>0if x≤0 其中,α\alphaα 是一个非常小的常数(如 0.01),控制负半轴的斜率。 |
| 特征 | 1. 当 x>0x > 0x>0 时,Leaky ReLU(x) = x。 2. 当 x≤0x \leq 0x≤0 时,Leaky ReLU(x) = αx\alpha xαx,其中 α\alphaα 是一个小的负斜率。 3. 计算简单,与 ReLU 类似,只需简单的比较和线性运算。 |
| 优点 | 1. 避免神经元死亡:通过在 x≤0x \leq 0x≤0 区域引入一个小的负斜率,即使输入值小于等于零,Leaky ReLU 仍然会有梯度,允许神经元继续更新权重,避免神经元在训练过程中完全“死亡”的问题。 2. 计算简单:与 ReLU 类似,计算开销低。 |
| 缺点 | 1. 参数选择:α\alphaα 是一个需要调整的超参数,选择合适的 α\alphaα 值可能需要实验和调优。 2. 可能出现负激活:如果 α\alphaα 设定得不当,仍然可能导致激活值过低,影响网络的性能。 |
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt# 中文设置
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = Falsedef test006():x = torch.linspace(-5, 5, 200)# 设置leaky_relu的负斜率超参数slope = 0.03y = F.leaky_relu(x, slope)# 一行两列_, ax = plt.subplots(1, 2)# 开始绘制函数曲线图ax[0].plot(x, y)ax[0].set_title("Leaky ReLU 函数曲线图")ax[0].set_xlabel("x")ax[0].set_ylabel("y")ax[0].grid(True)# 绘制leaky_relu的梯度曲线图x = torch.linspace(-5, 5, 200, requires_grad=True)F.leaky_relu(x, slope).sum().backward()ax[1].plot(x.detach().numpy(), x.grad)ax[1].set_title("Leaky ReLU 梯度曲线图", color="red")ax[1].set_xlabel("x")ax[1].set_ylabel("x.grad")ax[1].grid(True)# 设置线的颜色ax[1].lines[0].set_color("red")plt.show()if __name__ == "__main__":test006()
2.5 softmax
Softmax激活函数通常用于分类问题的输出层,它能够将网络的输出转换为概率分布,使得输出的各个类别的概率之和为 1。Softmax 特别适合用于多分类问题。
| 方面 | 内容 |
|---|---|
| 定义 | Softmax(zi)=ezi∑j=1nezj\mathrm{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}Softmax(zi)=∑j=1nezjezi |
| 特征 | 1. 将输出转化为概率分布,每个输出值在 (0, 1) 之间,且所有输出值之和为 1。 2. 突出差异,使得概率最大的类别的输出值更接近 1,其他类别更接近 0。 3. 常与交叉熵损失函数结合使用,用于多分类问题。 4. 导数计算:当 i=ji = ji=j 时,∂pi∂zi=pi(1−pi)\frac{\partial p_i}{\partial z_i} = p_i(1 - p_i)∂zi∂pi=pi(1−pi);当 i≠ji \neq ji=j 时,∂pi∂zj=−pipj\frac{\partial p_i}{\partial z_j} = -p_i p_j∂zj∂pi=−pipj。 |
| 优点 | 1. 概率化输出:将网络输出转化为概率分布,便于分类决策。 2. 突出差异:放大差异,使得最大概率值更接近 1,其他值更接近 0。 3. 数学性质良好:导数计算简单,适合多分类问题。 |
| 缺点 | 1. 数值不稳定性:当 ziz_izi 的数值过大时,ezie^{z_i}ezi 可能导致数值溢出。可以通过减去最大值 max(z)\max(z)max(z) 来解决:Softmax(zi)=ezi−max(z)∑j=1nezj−max(z)\mathrm{Softmax}(z_i) = \frac{e^{z_i - \max(z)}}{\sum_{j=1}^n e^{z_j - \max(z)}}Softmax(zi)=∑j=1nezj−max(z)ezi−max(z)。 2. 计算开销大:在处理大量类别时(如大词汇表),计算开销较大。 |
import torch
import torch.nn as nn# 表示4分类,每个样本全连接后得到4个得分,下面示例模拟的是两个样本的得分
input_tensor = torch.tensor([[-1.0, 2.0, -3.0, 4.0], [-2, 3, -3, 9]])softmax = nn.Softmax()
output_tensor = softmax(input_tensor)
# 关闭科学计数法
torch.set_printoptions(sci_mode=False)
print("输入张量:", input_tensor)
print("输出张量:", output_tensor)
