DAY17 常见聚类算法

@浙大疏锦行

知识点回顾

1.聚类的指标

1.1 轮廓系数 (Silhouette Score)

• 定义：轮廓系数衡量每个样本与其所属簇的紧密程度以及与最近其他簇的分离程度。
• 取值范围：[-1, 1]
  • 轮廓系数越接近 1，表示样本与其所属簇内其他样本很近，与其他簇很远，聚类效果越好。
  • 轮廓系数越接近 - 1，表示样本与其所属簇内样本较远，与其他簇较近，聚类效果越差（可能被错误分类）。
  • 轮廓系数接近 0，表示样本在簇边界附近，聚类效果无明显好坏。
• 使用建议：选择轮廓系数最高的 k 值作为最佳簇数量。

1.2 CH 指数 (Calinski-Harabasz Index)

• 定义：CH 指数是簇间分散度与簇内分散度之比，用于评估簇的分离度和紧凑度。
• 取值范围：[0, +∞)
  • CH 指数越大，表示簇间分离度越高，簇内紧凑度越高，聚类效果越好。
  • 没有固定的上限，值越大越好。
• 使用建议：选择 CH 指数最高的 k 值作为最佳簇数量。

1.3 DB 指数 (Davies-Bouldin Index)

• 定义：DB 指数衡量簇间距离与簇内分散度的比值，用于评估簇的分离度和紧凑度。
• 取值范围：[0, +∞)
  • DB 指数越小，表示簇间分离度越高，簇内紧凑度越高，聚类效果越好。
  • 没有固定的上限，值越小越好。
• 使用建议：选择 DB 指数最低的 k 值作为最佳簇数量。

2.聚类常见算法

2.1 KMeans 聚类

算法原理
KMeans 是一种基于距离的聚类算法，需要预先指定聚类个数，即 k。其核心步骤如下：

1. 随机选择 k 个样本点作为初始质心（簇中心）。
2. 计算每个样本点到各个质心的距离，将样本点分配到距离最近的质心所在的簇。
3. 更新每个簇的质心为该簇内所有样本点的均值。
4. 重复步骤 2 和 3，直到质心不再变化或达到最大迭代次数为止。

确定簇数的方法：肘部法

• 肘部法（Elbow Method）是一种常用的确定 k 值的方法。
• 原理：通过计算不同 k 值下的簇内平方和（Within-Cluster Sum of Squares, WCSS），绘制 k 与 WCSS 的关系图。
• 选择标准：在图中找到 “肘部” 点，即 WCSS 下降速率明显减缓的 k 值，通常认为是最佳簇数。这是因为增加 k 值带来的收益（WCSS 减少）在该点后变得不显著。

KMeans 算法的优缺点
优点

• 简单高效：算法实现简单，计算速度快，适合处理大规模数据集。
• 适用性强：对球形或紧凑的簇效果较好，适用于特征空间中簇分布较为均匀的数据。
• 易于解释：聚类结果直观，簇中心具有明确的物理意义。

缺点

• 需预先指定 k 值：对簇数量 k 的选择敏感，不合适的 k 会导致聚类效果较差。
• 对初始质心敏感：初始质心的随机选择可能导致结果不稳定或陷入局部最优（可通过 KMeans++ 初始化方法缓解）。
• 对噪声和异常值敏感：异常值可能会显著影响质心的位置，导致聚类结果失真。
• 不适合非球形簇：对非线性可分或形状复杂的簇效果较差，无法处理簇密度不均的情况。

 

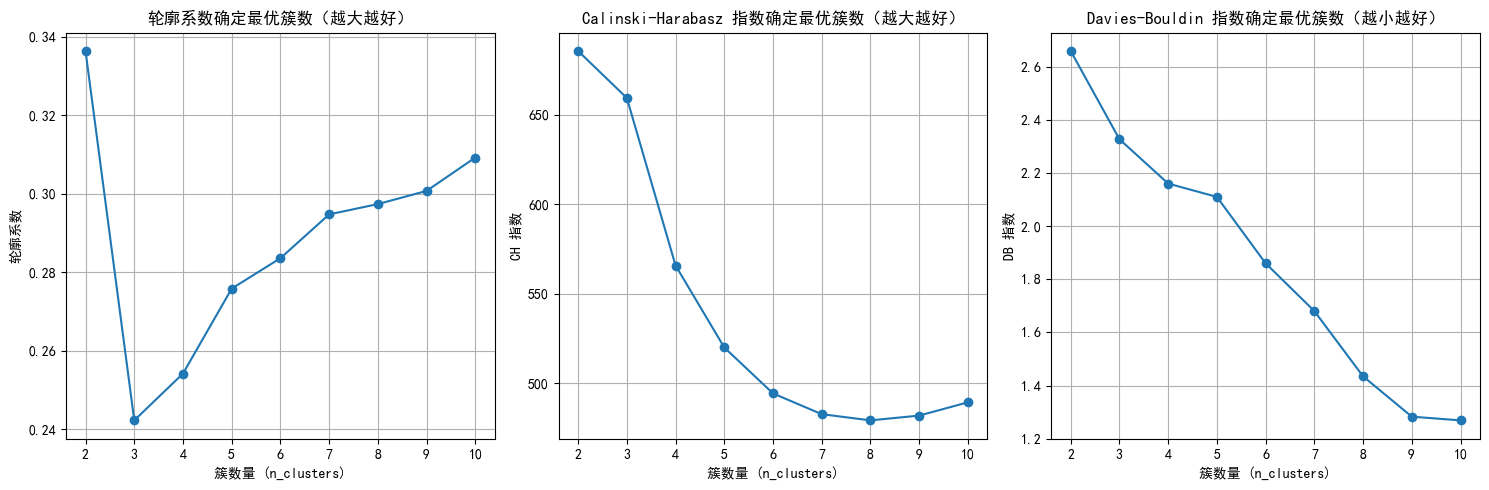
我和大家说下上面这几个图怎么看，

1. 肘部法则图： 找下降速率变慢的拐点，这里都差不多

2. 轮廓系数图：找局部最高点，这里选6不能选7

3. CH指数图： 找局部最高点，这里选7之前的都还行

4. DB指数图：找局部最低点，这里选6 7 9 10都行

综上，选择6比较合适。

- 为什么选择局部最优的点，因为比如簇间差异，分得越细越好，但是k太细了没价值，所以要有取舍。

- 比如k可以选3和5，推荐选择5，能包含更多信息

2.2 DBSCAN聚类 

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，它不需要预先指定簇的数量，能够自动发现任意形状的簇，并识别出噪声点。其核心思想是：簇是由足够高密度的区域组成的，同一簇内的样本点之间是密度可达的，而不同簇之间被低密度区域（噪声）分隔。

一、核心概念

在理解 DBSCAN 算法前，需要先明确几个关键定义：

1. ε（Epsilon，邻域半径）
   用于定义 “邻域” 的范围，即一个样本点周围距离小于等于 ε 的所有点构成该样本的 “ε- 邻域”。

2. MinPts（最小样本数）
   判定一个区域是否为 “高密度区域” 的阈值：若一个样本的 ε- 邻域内包含的样本数（包括自身）大于等于 MinPts，则该样本被称为 “核心点”。

3. 核心点（Core Point）
   满足 “ε- 邻域内样本数 ≥ MinPts” 的样本点，是构成簇的核心元素。

4. 边界点（Border Point）
   不满足核心点条件，但落在某个核心点的 ε- 邻域内的样本点。边界点属于其所在的核心点对应的簇，但自身无法作为核心点扩展簇。

5. 噪声点（Noise Point）
   既不是核心点，也不落在任何核心点的 ε- 邻域内的样本点，最终会被判定为噪声，不归属任何簇。

6. 密度可达（Density-Reachable）
   若存在一条核心点链（p1→p2→…→pn），其中每个点都在前者的 ε- 邻域内，且 p1 是核心点，则称 pn 从 p1 “密度可达”。同一簇内的所有点之间都是密度可达的。

7. 密度相连（Density-Connected）
   若存在一个核心点 o，使得点 p 和点 q 都从 o 密度可达，则 p 和 q “密度相连”。密度相连的点属于同一簇。

二、算法步骤

DBSCAN 的聚类过程可概括为 “基于核心点扩展簇”，具体步骤如下：

1. 遍历数据集中的每个样本点，根据 ε 和 MinPts 判断其是否为核心点。
2. 对每个未被分类的核心点，以其为起点，将所有从它密度可达的样本点（包括核心点和边界点）划分为一个簇。
3. 若样本点是边界点且已被划分到某个簇，则不再处理；若未被划分，需检查其所在的核心点对应的簇，将其归入该簇。
4. 所有样本点处理完毕后，未被归入任何簇的点即为噪声点。

简单来说，DBSCAN 通过核心点 “扩张” 形成簇：核心点像 “种子” 一样，不断将其 ε- 邻域内的点纳入簇中，直到没有新的点可以被纳入，最终形成一个完整的簇；而噪声点因周围没有足够密集的样本，无法形成簇。

三、参数选择（ε 和 MinPts 的确定）

DBSCAN 的聚类效果严重依赖于参数 ε 和 MinPts 的选择，需根据数据特点调整：

1. ε 的选择
   常用方法是 “k - 距离法”：计算每个样本到其第 k 个最近邻样本的距离，绘制 “k - 距离曲线”，选择曲线中 “拐点” 对应的距离作为 ε（拐点处距离突然增大，代表多数样本的邻域范围在此处边界）。通常 k 可设为 MinPts-1（与 MinPts 对应）。

2. MinPts 的选择
   一般根据数据集的维度（d）设定，经验值为 MinPts = d + 1（如二维数据可设为 3）。若数据噪声较多，可适当增大 MinPts 以过滤噪声；若数据稀疏，可减小 MinPts。

四、优缺点

优点

1. 无需预先指定簇数 k
   算法能自动根据数据密度确定簇的数量，避免了 KMeans 中 k 值选择的难题。

2. 能识别噪声
   明确区分噪声点，适合处理含噪声的数据。

3. 可处理任意形状的簇
   对非球形、不规则形状（如环形、条形）的簇聚类效果较好，优于 KMeans 等基于距离的算法。

4. 对数据分布适应性强
   能处理密度不均的簇（只要同一簇内密度足够高）。

缺点

1. 对参数 ε 和 MinPts 敏感
   不同的 ε 和 MinPts 可能导致完全不同的聚类结果，且参数选择没有统一标准，需结合领域知识或多次实验调整。

2. 对高维数据效果较差
   高维空间中 “距离” 的定义变得模糊（维度灾难），ε- 邻域的意义被削弱，可能导致核心点难以识别。

3. 计算复杂度较高
   基本实现的时间复杂度为 O (n²)（n 为样本数），对大规模数据集效率较低（可通过空间索引如 KD 树优化，但仍不及 KMeans）。

4. 对密度差异大的簇处理不佳
   若数据中存在密度差异显著的簇（如一个簇密集、一个簇稀疏），同一组 ε 和 MinPts 可能无法同时适配两个簇（密集簇需要小 ε，稀疏簇需要大 ε）。

 eps=0.3, min_samples=3, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.3, min_samples=4, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.3, min_samples=5, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.3, min_samples=6, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.3, min_samples=7, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.4, min_samples=3, 簇数: 1, 噪声点: 7497, 无法计算评估指标
eps=0.4, min_samples=4, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.4, min_samples=5, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.4, min_samples=6, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.4, min_samples=7, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.5, min_samples=3, 簇数: 21, 噪声点: 7420, 轮廓系数: 0.494, CH 指数: 89.64, DB 指数: 0.613
eps=0.5, min_samples=4, 簇数: 5, 噪声点: 7473, 轮廓系数: 0.463, CH 指数: 83.11, DB 指数: 0.749
eps=0.5, min_samples=5, 簇数: 1, 噪声点: 7495, 无法计算评估指标
eps=0.5, min_samples=6, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.5, min_samples=7, 簇数: 0, 噪声点: 7500, 无法计算评估指标
eps=0.6, min_samples=3, 簇数: 56, 噪声点: 7214, 轮廓系数: 0.267, CH 指数: 58.95, DB 指数: 0.953
eps=0.6, min_samples=4, 簇数: 21, 噪声点: 7356, 轮廓系数: 0.306, CH 指数: 72.52, DB 指数: 0.988
eps=0.6, min_samples=5, 簇数: 7, 噪声点: 7433, 轮廓系数: 0.347, CH 指数: 42.56, DB 指数: 0.988
eps=0.6, min_samples=6, 簇数: 6, 噪声点: 7452, 轮廓系数: 0.414, CH 指数: 48.32, DB 指数: 0.843
eps=0.6, min_samples=7, 簇数: 2, 噪声点: 7486, 轮廓系数: 0.758, CH 指数: 109.90, DB 指数: 0.318
eps=0.7, min_samples=3, 簇数: 90, 噪声点: 6800, 轮廓系数: 0.028, CH 指数: 22.65, DB 指数: 0.918
eps=0.7, min_samples=4, 簇数: 39, 噪声点: 7047, 轮廓系数: -0.026, CH 指数: 20.20, DB 指数: 0.955
eps=0.7, min_samples=5, 簇数: 15, 噪声点: 7214, 轮廓系数: -0.013, CH 指数: 26.35, DB 指数: 1.010
eps=0.7, min_samples=6, 簇数: 5, 噪声点: 7313, 轮廓系数: 0.015, CH 指数: 25.90, DB 指数: 1.101
eps=0.7, min_samples=7, 簇数: 5, 噪声点: 7337, 轮廓系数: 0.035, CH 指数: 26.04, DB 指数: 1.337

 

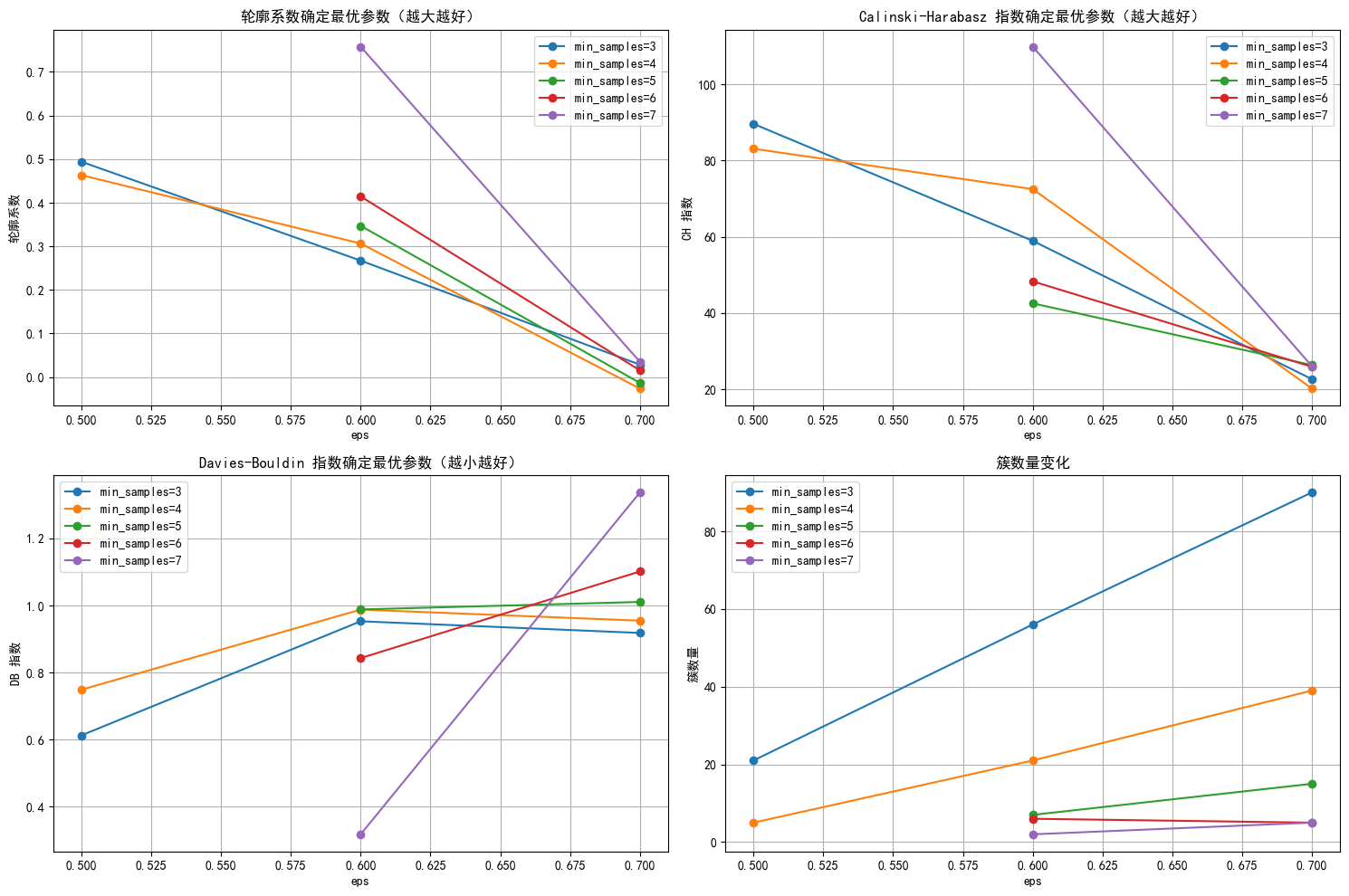
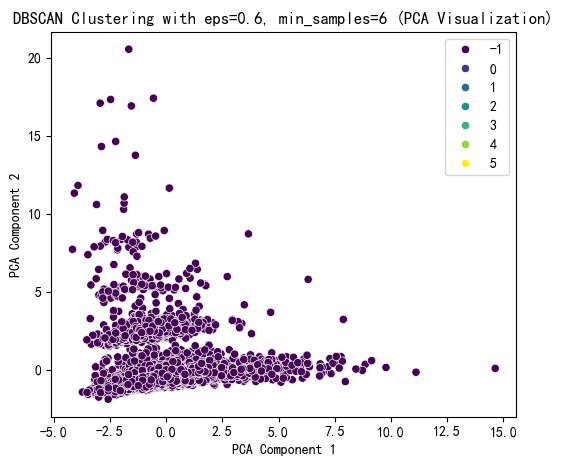
从结果来看 这个聚类是失败的 因为没有少数簇的数目太少，也可能是dbscan这个算法不太合适 

 2.3 层次聚类

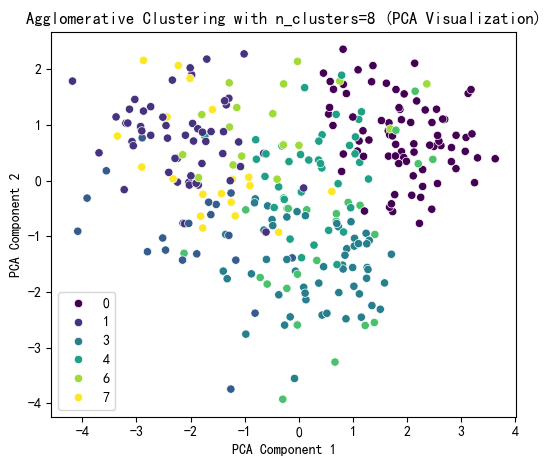
Agglomerative Clustering 是一种自底向上的层次聚类方法，初始时每个样本是一个簇，然后逐步合并最相似的簇，直到达到指定的簇数量或满足停止条件。由于它需要指定簇数量（类似于 KMeans），我将通过测试不同的簇数量 n_clusters 来评估聚类效果，并使用轮廓系数（Silhouette Score）、CH 指数（Calinski-Harabasz Index）和 DB 指数（Davies-Bouldin Index）作为评估指标。

 

 

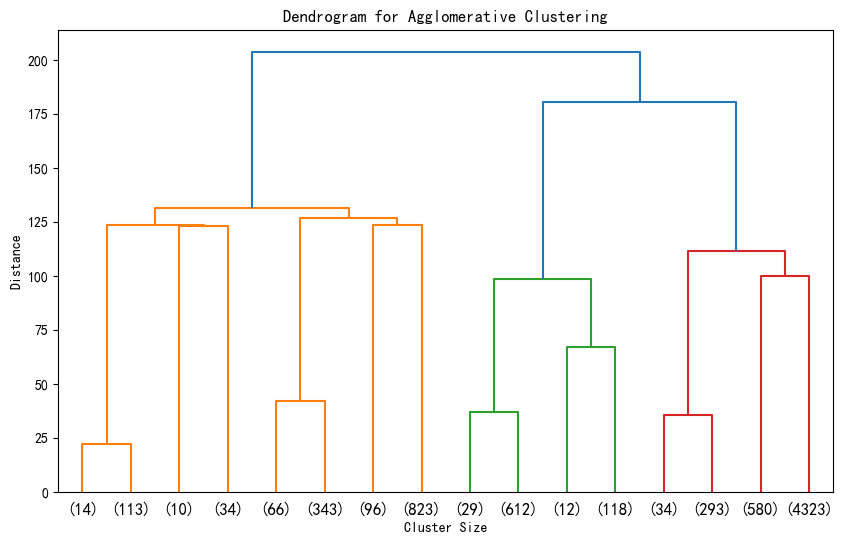
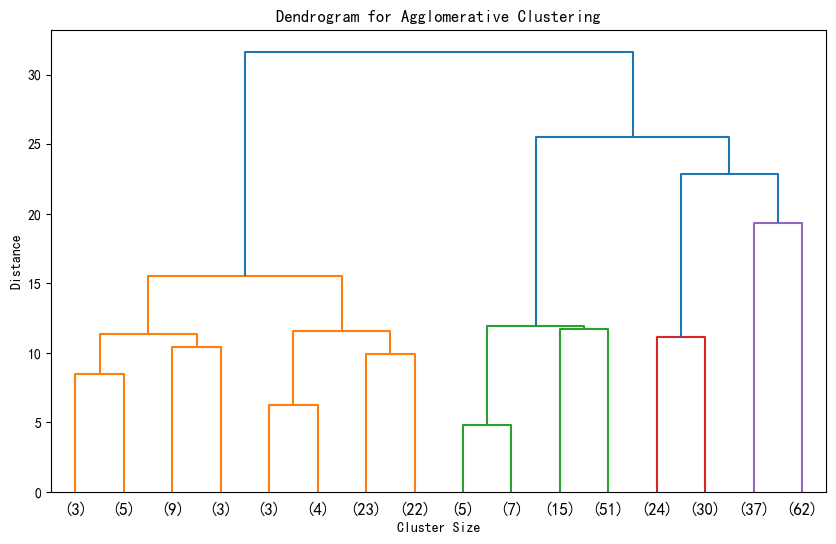
1. 横坐标代表每个簇对应样本的数据，这些样本数目加一起是整个数据集的样本数目。这是从上到下进行截断，p=3显示最后3层，不用p这个参数会显示全部。

2. 纵轴代表距离 ，反映了在聚类过程中，不同样本或簇合并时的距离度量值。距离越大，意味着两个样本或簇之间的差异越大；距离越小，则差异越小。

作业

 

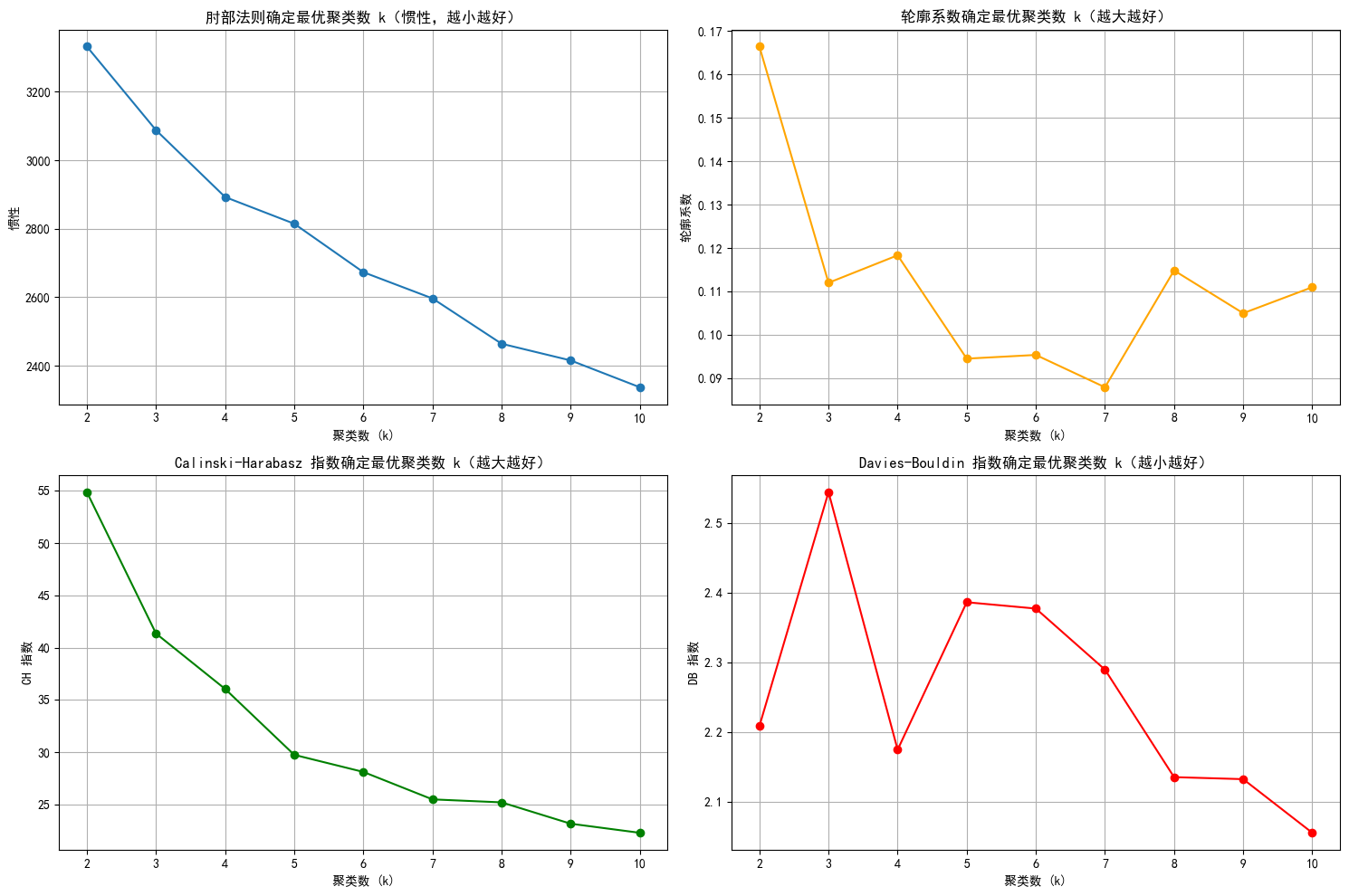
逐图分析 & 交叉验证

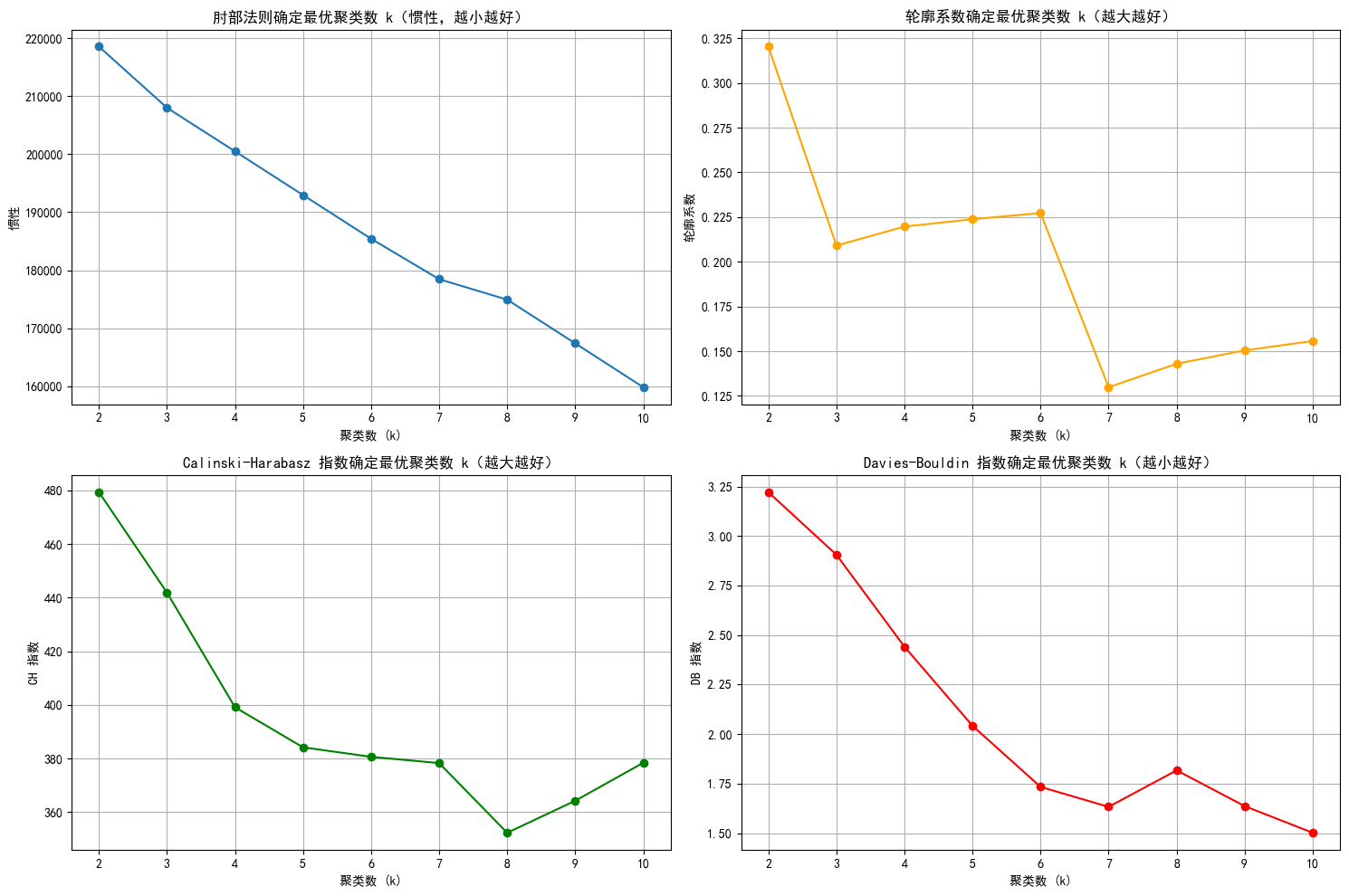
• 肘部法：看蓝色折线，k=3 或 k=4 附近有 “肘部” 趋势（WCSS 下降速率明显放缓），初步标记候选。
• 轮廓系数：黄色折线在 k=2 最高，但 k=2 可能太粗颗粒；k=6 前后也有相对高值，需结合其他指标。
• CH 指数：绿色折线 k=2 最高，k>2 后快速下降，k=2 看似最优，但需警惕 “过拟合”（簇数太少丢失细节）。
• DB 指数：红色折线 k=10 最低，但 k=10 可能簇太碎；k=6 或 k=7 也处于低值区间，可关注。

综合决策逻辑

• 优先看 “共识”：若多个指标指向同一 k，优先选。比如：
  • 若业务需要 “大簇、少分类”，k=2 或 k=3 可考虑（肘部法、CH 指数支持，但轮廓系数 k=2 高，实际看业务场景是否接受粗分类）。
  • 若追求 “更细分、高质量簇”，看 k=6 左右：
    • 肘部法 k=4 后下降趋缓，k=6 算合理；
    • 轮廓系数 k=6 分数不差；
    • CH 指数 k=6 虽不如 k=2，但属于 “下降后相对平稳” 区间；
    • DB 指数 k=6 处于低值，聚类质量有保障。

综上选k=6

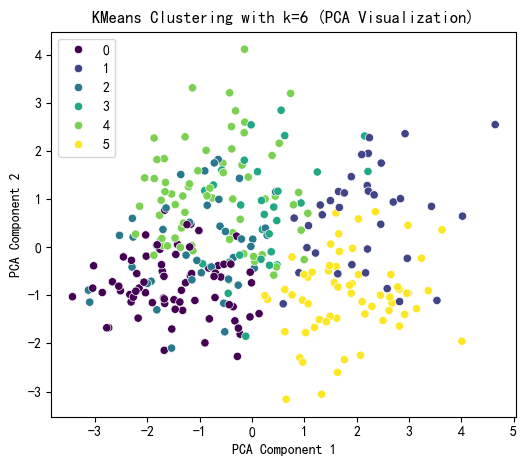
KMeans Cluster labels (k=6) added to X:
KMeans_Cluster
0                 71
4                 66
5                 61
2                 41
1                 35
3                 29
Name: count, dtype: int64

2. DBSCAN聚类

eps=0.3, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.3, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.4, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.5, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.6, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=3, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=4, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=5, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=6, 簇数: 0, 噪声点: 303, 无法计算评估指标
eps=0.7, min_samples=7, 簇数: 0, 噪声点: 303, 无法计算评估指标 

显然效果很差。

3.  层次聚类

 

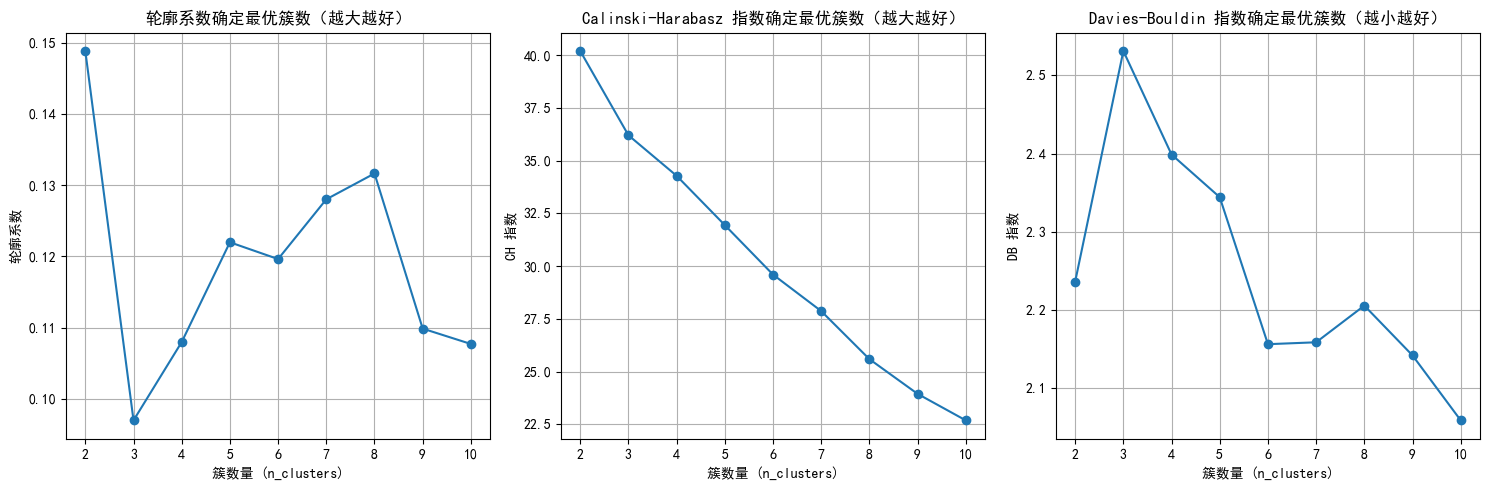
逐图分析候选 k

（1）轮廓系数（左图）

• 蓝色折线在 k=2 最高，但 k=2 可能过于粗略（簇数太少，丢失细节）；
• k=8 也有相对高值，需结合其他指标验证。

（2）CH 指数（中图）

• 绿色折线 k=2 最高，k>2 后持续下降；
• 但 k=2 可能 “过度简化”，需警惕簇数太少导致的信息丢失。

（3）DB 指数（右图）

• 红色折线 k=10 最低，但 k=10 可能簇太碎（过拟合，业务意义弱）；
• k=7/k=8 处于低值区间，k=10 虽低但需权衡业务实用性。

 交叉验证 & 决策逻辑

核心原则：找多个指标 “共识” 的 k，或业务可解释的 k

（1）排除极端值

• k=2：CH 指数、轮廓系数高，但簇数太少，实际场景中分类太粗，除非业务明确需要 “二分”，否则不优先选。
• k=10：DB 指数最低，但簇数过多，业务中难解释（比如客户分 10 类，管理成本高），除非数据天然极细分，否则谨慎选。

（2）看 “平衡区间”

关注 k=7/k=8/k=9：

• 轮廓系数：k=8 相对高，k=7/k=9 中等；
• CH 指数：k=7/k=8 虽不如 k=2，但处于 “下降后平稳” 区间；
• DB 指数：k=7/k=8 低值，聚类质量有保障。

（3）业务导向验证

• 若业务需要 “适度细分、可解释”：优先选 k=7 或 k=8（DB 低、轮廓系数不差，簇质量平衡）。
• 若追求 “更高区分度”：k=8 更优（轮廓系数相对高，CH 指数、DB 指数也适配）。

综上选取k=8。