LinkedList与链表(单向)(Java实现)
引入链表结构:
一:链表
1:结构:

链表中的元素可以抽象为对象,每一个对象包含一个val值与next值,next就是指向下一个节点的地址。,这样就实现了虽然物理上不连续,但是逻辑上实现了连续。
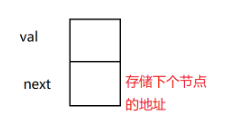

演示:
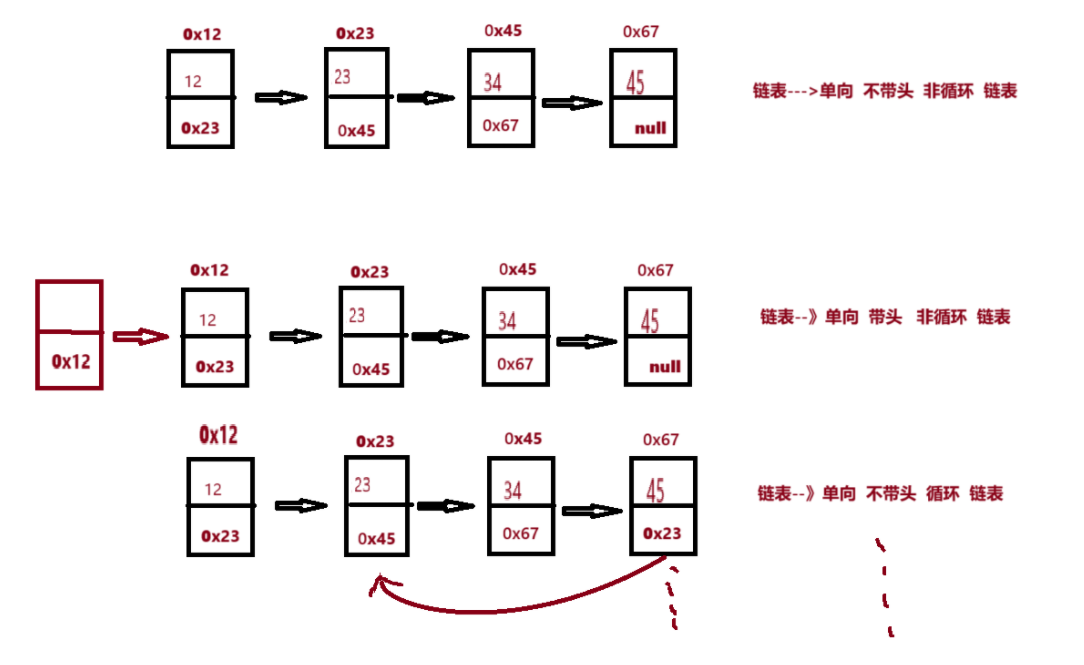
链表结构一共8中,分别是:
单向 带头 非循环 单向 不带头 非循环 双向 不带头 非循环 双向 不带头 循环
单向 带头 循环 单向 不带头 循环 双向 带头 非循环 双向 带头 循环
2:实现:
对链表的增删该查方法进行手动实现:
将链表抽象为对象,每一个对象中都包含一个val值与next值,将val与next初始化为内部类的成员属性,通过构造方法对传输的val值进行初始化,这样传输的val值就带有一个next属性,成为了一个对象。
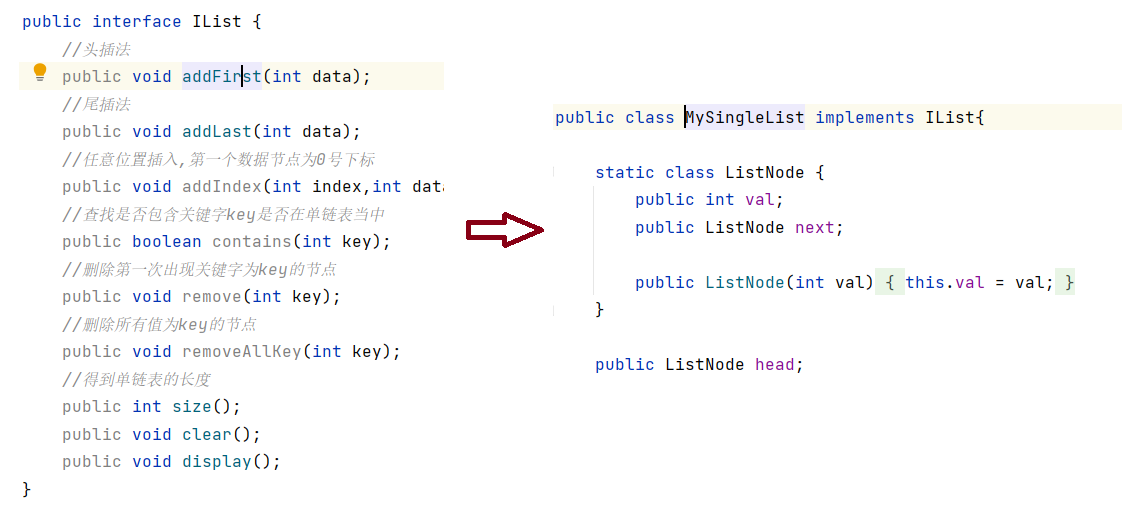 代码解释:
代码解释:
next 是一个指向同类对象的引用:
1: 它存储内存中下一个节点对象的内存地址
2: 类型为 ListNode 表示它只能指向另一个 ListNode 类型的对象
3: 最后一个节点的 next 通常设为 null(表示链表结束)
public ListNode head; 的含义:
1:head:变量名,表示链表的头节点(链表的起始点)
2:返回ListNode对象,相当于这个head是一个ListNode对象,包含val属性与next属性(链 表由节点组成,头节点是链表的起点)
ListNode 作为返回类型意味着什么?
1: 返回的是对ListNode 对象的引用(reference)
2 : 引用本质上是对象的句柄,包含:
2.1 对象的内存地址(但 Java 不直接暴露地址)
2.2 通过引用可以访问对象的完整状态(字段)和行为(方法)
初始化对象:
当使用 new Node(value) 时:new 操作符在堆内存中分配空间创建新对象 → 生成新地址
然后调用构造方法初始化对象状态
最后返回该对象的引用(地址)

2.1:创建一个链表
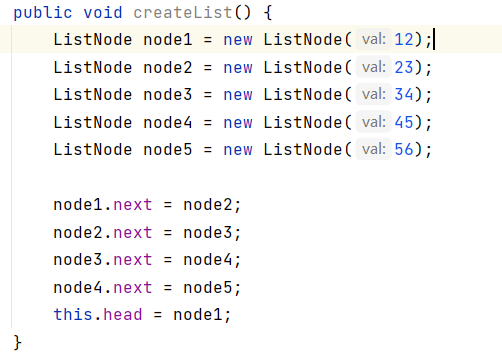
ListNode node=new ListNode(val): 调用ListNode内部类,传入val值,然后调用构造方法初始化对象,最后形成链表(对象)。
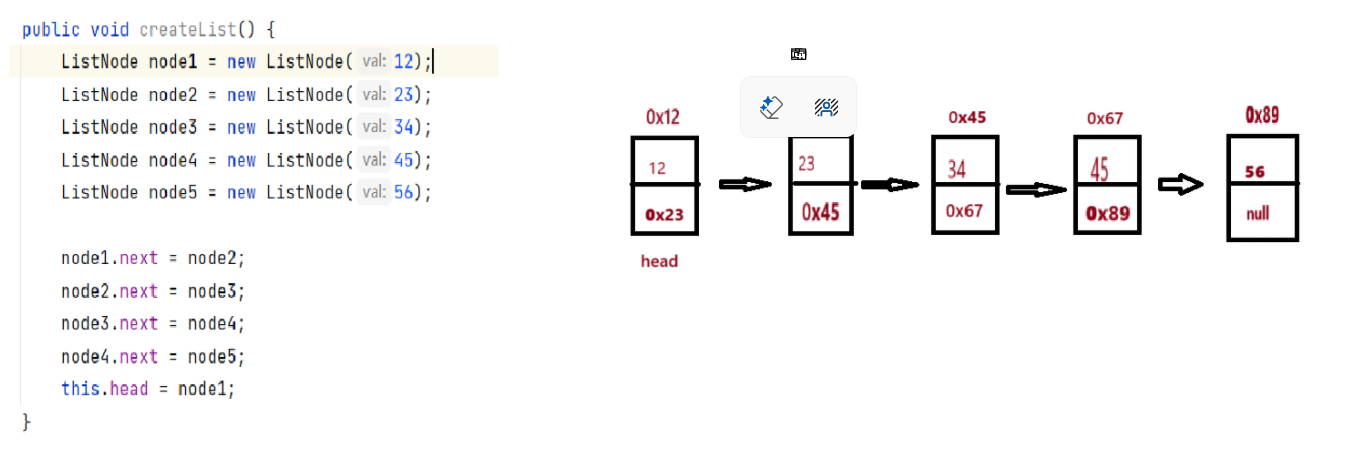
2.2:display(打印链表)

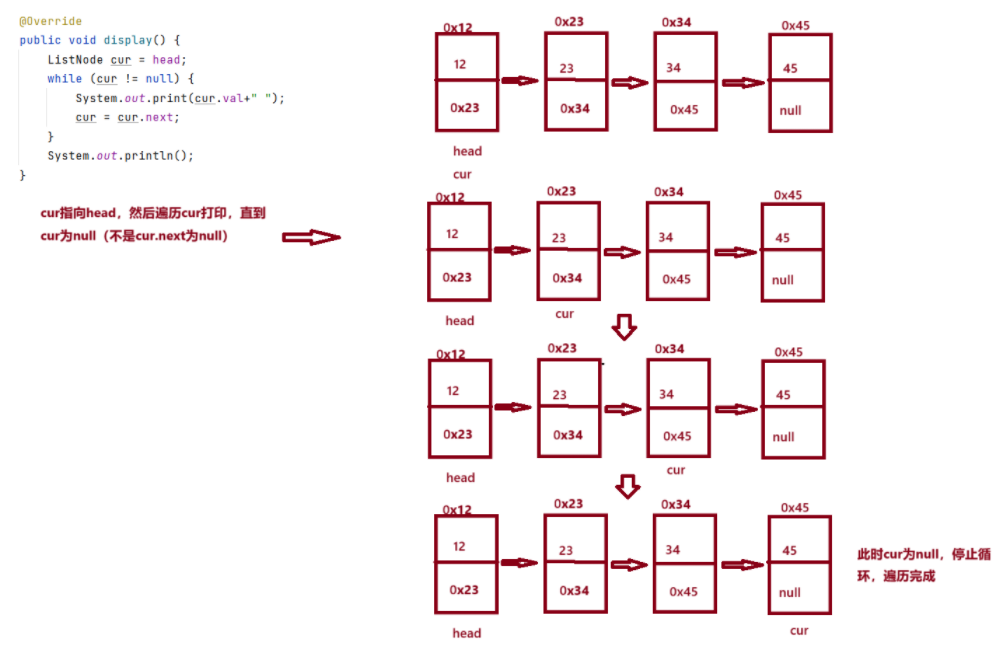
2.3:size(链表长度)
逐一遍历直到cur为null,也就是遍历完最后一个节点,最后一个节点的next的节点为null时,停止遍历,返回len。

2.4:findNodeOfKey(查找)
遍历cur,直到cur的val为key时,返回cur。

图示:
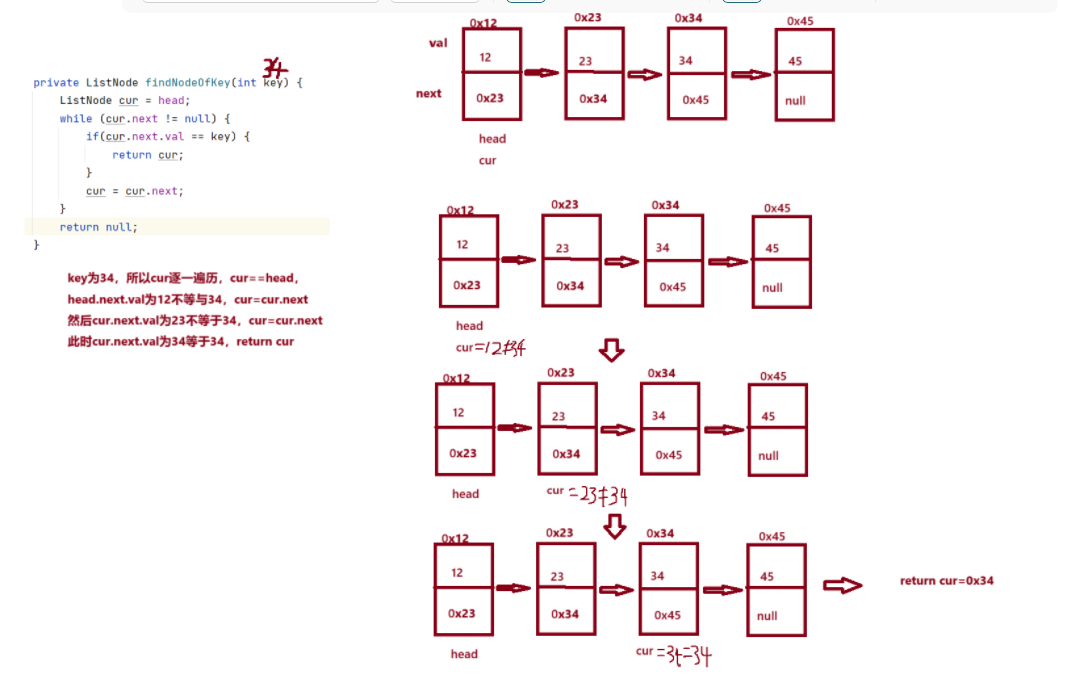
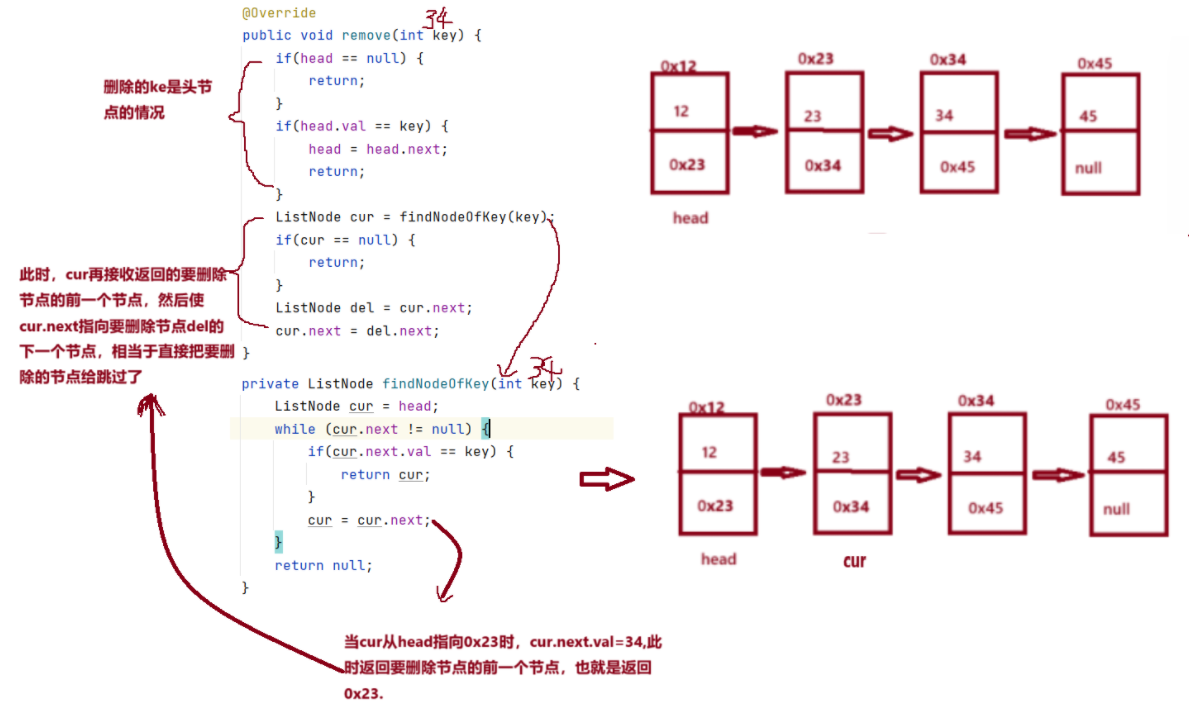
2.5: remove(删除一个指定元素)
首先保证存在链表,如果要删除的key值为头节点,然后使head节点指向下一个节点,如果不是头节点则执行逻辑代码,先找到要删除节点的前一个节点,然后del保存为要删除节点的下一个节点,使cur.next指向要删除节点的下一个节点,这样要删除的节点直接被跳过了。
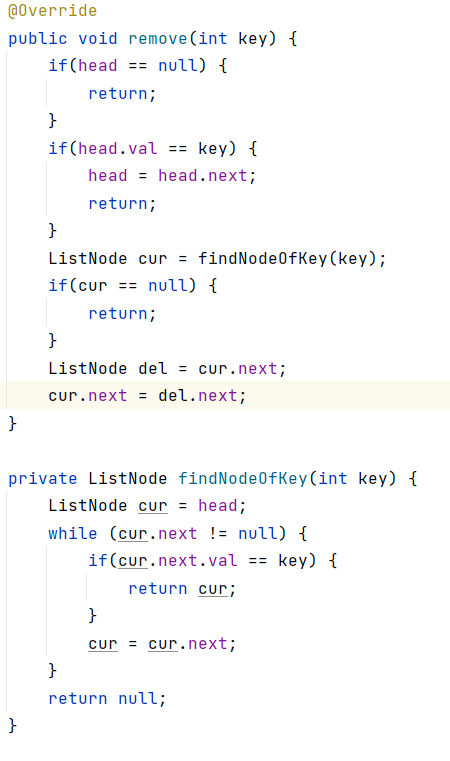
图示展示:
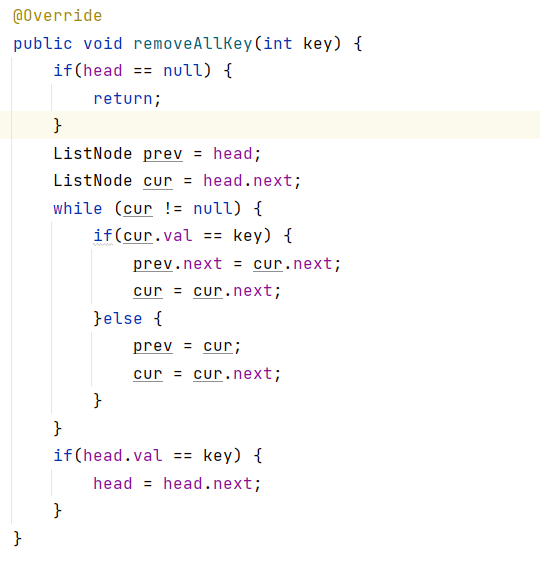
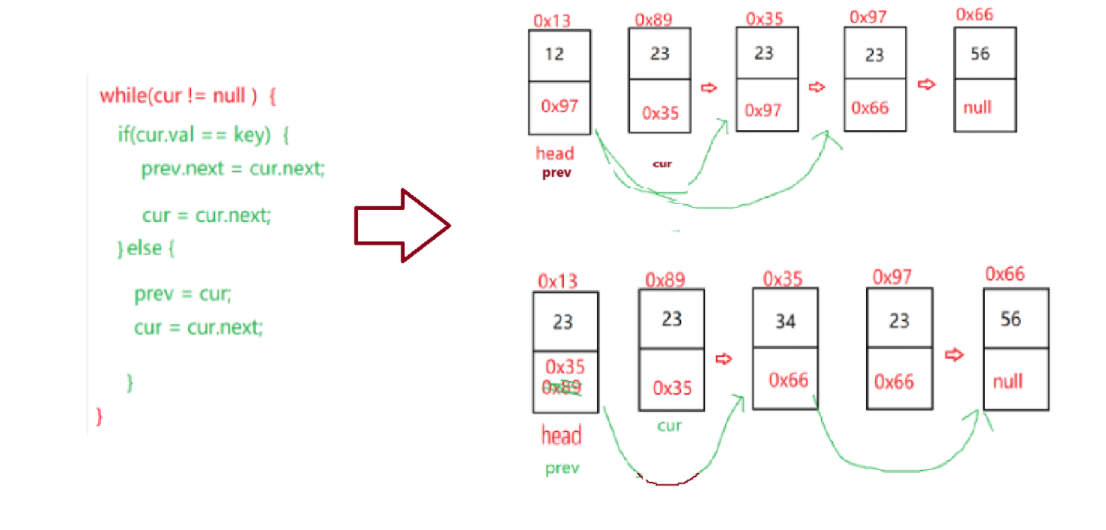
2.6:removeAllKey(删除所有为key值的节点)
如果要删除的节点正好是head节点指向的下一个节点,那么执行if语句,删除(跳过)这个节点,使head指向它的next.next的节点,然后prev指向此时的cur,也就是被跳过的节点,然后cur指向cur的下一个节点,循环执行,如果要删除的节点包含头节点,那么最后删除(跳过)头节点,最后处理,不要先处理。
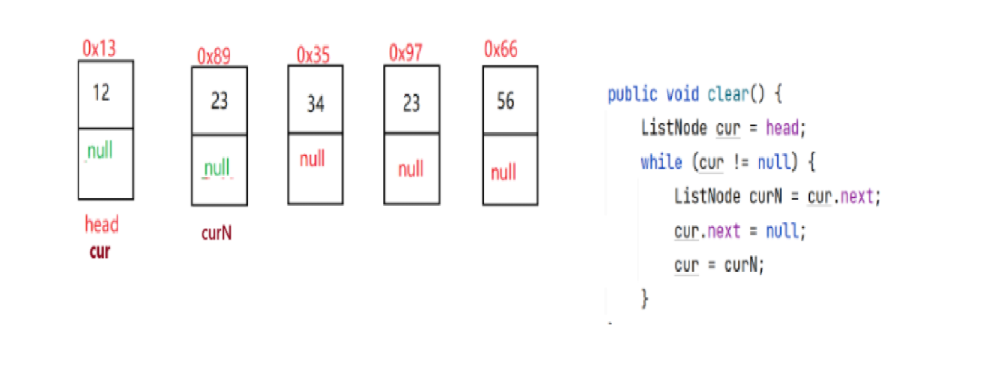
2.7:clear(删除所有节点)
删除所有节点可以直接将head==null这样链表就没有了头,其他节点也就自动被清理了。
也可以一个一个的将节点置为null。

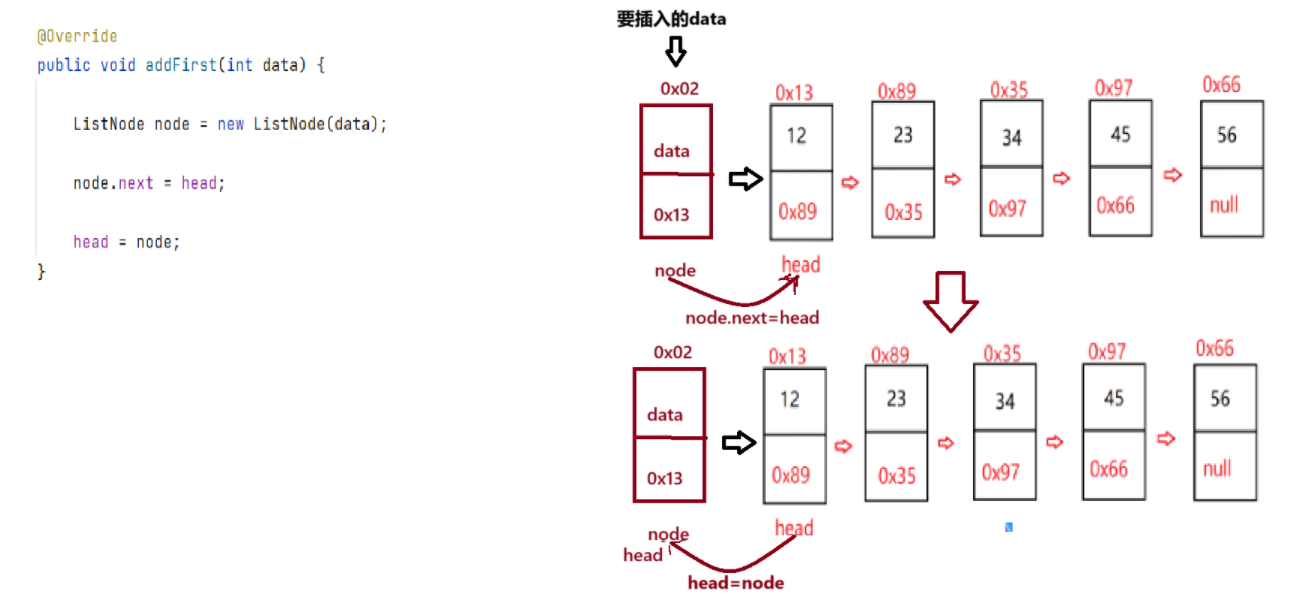
2.8:addFirst(头插)
将传输的data初始化为节点对象,调用构造方法,生成node对象,然后将node的下一个节点指向head节点,此时head节点使第二个节点,最后再将head置为第一个节点指向node。

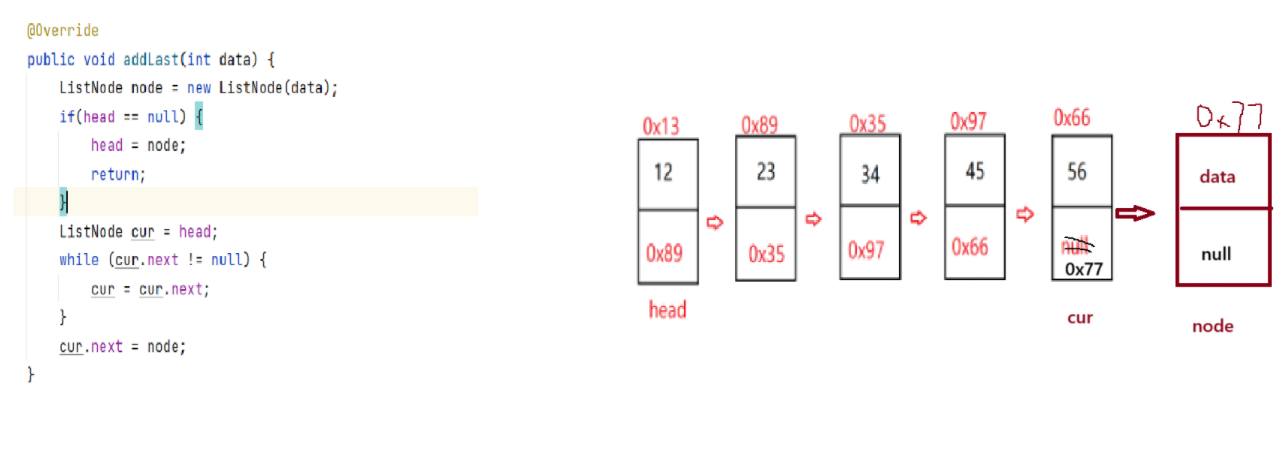
2.9:addLast(尾插法)
同理,生成node对象,先遍历到最后一个节点,然后将node插入到最后,此时cur==null,然后将cur.next=node,这样就再最后插入了node。

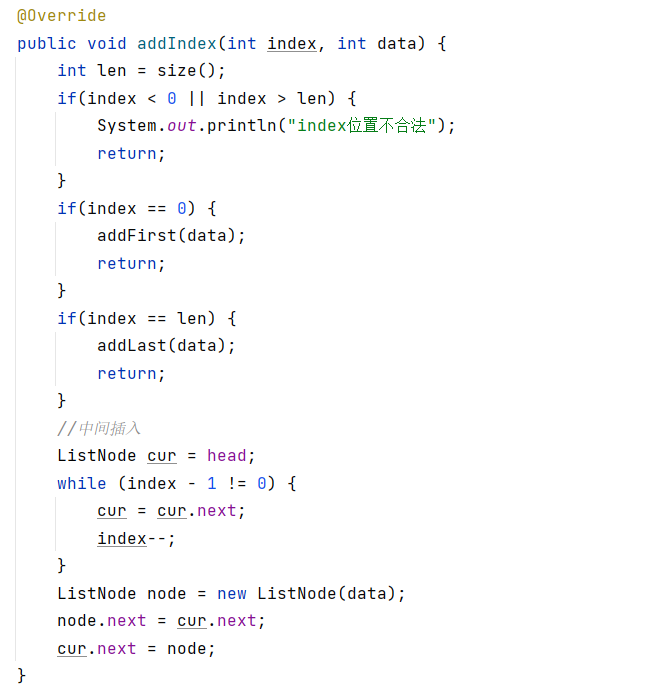
2.10:addIndext(在任意位置插入)
首先确保插入位置合法,不超过链表的长度,也不为负数,也就是在index位置插入data值,那么cur需要走到index节点的前一个节点,也就是要走index-1步
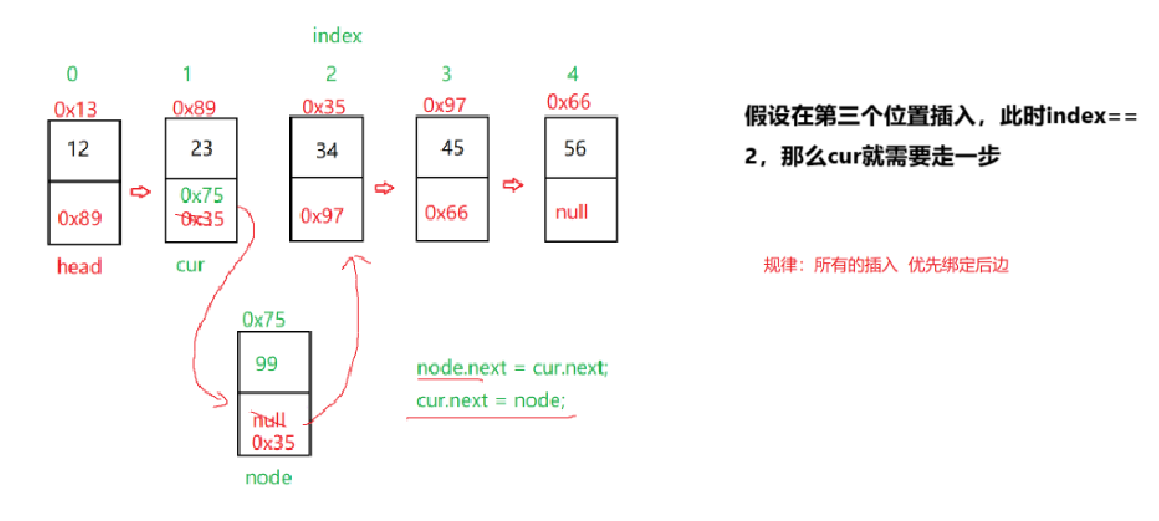
2.11:contain(包含某个节点)
遍历cur,从头节点开始,直到找到key的值,找到返回true,没有找到返回false

物理连续与逻辑连续:
物理存储结构:指的是数据元素(节点)实际在计算机内存(或存储介质)中占据的位置。
物理上连续的存储结构: 最典型的例子就是数组。
如何连续: 当你创建一个数组(例如
int arr[10];)时,操作系统或运行环境会在内存中找出一块连续的空闲区域,大小刚好能容纳10个整数(假设每个int占4字节,就是40字节的连续空间)。地址关系: 数组的第一个元素
arr[0]占据某个起始地址(比如0x1000),那么arr[1]紧挨着它,地址是0x1004(假设int是4字节),arr[2]在0x1008,以此类推,直到arr[9]在0x1024。这些元素的内存地址在数值上是连续的、紧密相邻的。特点: 知道第一个元素的地址和每个元素的大小,就能通过简单的算术运算(
起始地址 + 索引 * 元素大小)直接计算出任何一个元素的物理地址,实现快速随机访问(O(1)时间复杂度)。
物理上非连续的存储结构: 最典型的例子就是链表。
如何非连续: 当你创建链表的节点时,每次创建一个新节点(
Node),系统只是在当前可用的任意空闲内存位置分配空间给这个节点。它完全不关心之前创建的节点或之后将要创建的节点在内存的哪个位置。地址关系: 假设链表有3个节点 A、B、C,逻辑顺序是 A -> B -> C。
节点 A 可能被分配到地址
0x2000。节点 B 可能被分配到地址
0x5000(很远,与 A 不连续)。节点 C 可能又被分配到
0x3000(在 A 和 B 之间,也不连续)。这些节点的内存地址在数值上没有任何规律,是随机分散在内存中的,彼此之间不是紧挨着的。
特点: 你无法通过起始地址和索引计算出某个节点的物理地址。节点的物理位置是随机的。
