腾讯二面手撕题:BatchNorm和LayerNorm
题目
辨析批量归一化(Batch Normalization,BN)和层归一化(Layer Normalization,LN),并不调包进行代码实现。
解答
核心目标:
归一化技术的根本目的是解决深度神经网络训练过程中的 内部协变量偏移(Internal Covariate Shift, ICS) 问题。
什么是 ICS?
在训练过程中,随着网络参数的更新,每一层输入的分布(均值、方差)会发生变化。这是因为前一层的参数更新改变了其输出分布,而这个输出就是后一层的输入。深层的网络需要不断适应这种输入分布的变化,导致:训练不稳定: 需要更小的学习率和精细的参数初始化。
训练速度慢: 网络需要更多迭代次数来适应分布变化。
梯度问题: 可能导致梯度消失或爆炸。
归一化如何解决 ICS?
归一化层被插入到网络的激活函数之前(或线性层之后)。它强制该层的输入(或输出)具有稳定的分布(通常是零均值和单位方差),从而:减少对参数初始化的依赖。
允许使用更大的学习率,加速收敛。
具有一定的正则化效果(特别是 BatchNorm),有助于防止过拟合。
缓解梯度问题。
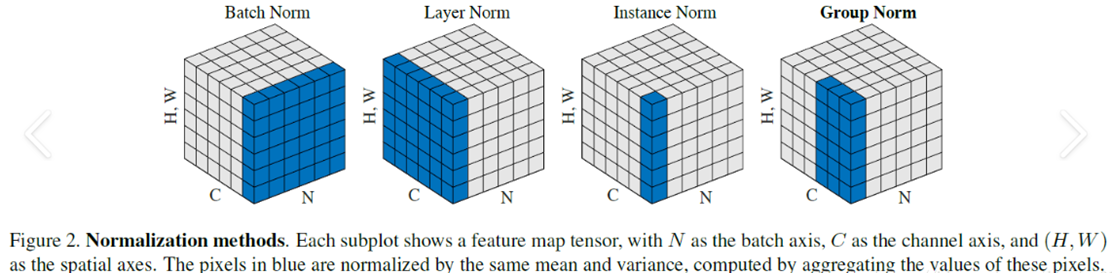
1. 批归一化(Batch Normalization, BN)
核心思想: 利用当前小批量(Mini-batch) 数据来计算该层输入的均值和方差,并进行归一化。BN 沿着 Batch 维度 进行归一化。
操作步骤: 对于一个维度为 (B, C, H, W) 的特征张量(B 是 batch size,C 是通道数,H 是高度,W 是宽度):
(1)计算均值和方差: 对每个通道 c,在整个 Batch 的 B 个样本以及每个样本的空间位置 (H, W) 上计算均值和方差。
均值: (在 B, H, W 维度上求平均)
方差: (在 B, H, W 维度上求方差)
结果得到长度为 C 的向量 μ 和 σ²。
(2)归一化: 对每个通道 c 的每个样本、每个空间位置的元素进行归一化:
其中ε 是一个很小的常数(如 1e-5),用于防止除以零。
(3)缩放与偏移(仿射变换): 引入两个可学习的参数 γ_c 和 β_c(每个通道一组),对归一化后的值进行缩放和偏移,以恢复网络的表示能力:
其中γ 初始化为 1,β 初始化为 0。网络可以学习决定是否保留归一化效果以及恢复到什么程度。
训练与推理:
- 训练: 使用当前 mini-batch 计算
μ和σ²。同时,使用指数移动平均(Exponential Moving Average, EMA) 累积计算整个训练集的全局均值和方差估计 (running_mean,running_var)。 - 推理: 不再依赖当前 batch。使用训练阶段累积的
running_mean和running_var代替μ和σ²进行归一化。γ和β使用训练好的固定值。
优点:
显著加速收敛: 允许使用更大的学习率。
减少对初始化的依赖: 对初始权重不太敏感。
正则化效果: 每个样本的归一化依赖于当前 batch 中的其他样本(引入了随机性),类似于 Dropout,有助于防止过拟合。
在 CNN 中效果卓越: 非常适合处理具有空间结构(H, W)且通道(C)独立的卷积特征图。
缺点/局限性:
依赖 Batch Size: 性能对 batch size 敏感。
小 Batch Size 问题: 当 batch size 很小时(如 1 或 2),计算出的
μ和σ²噪声大、不稳定,导致训练不稳定,性能下降。无法用于 Online Learning / 大模型训练: 某些场景下 batch size 必须为 1。
RNN/Transformer 不友好: RNN 处理的是变长序列,不同时间步的统计量难以用 BN 稳定计算。Transformer 不同样本序列长度不同,也存在类似问题。
推理与训练差异: 依赖 EMA 估计的全局统计量,可能与真实分布有偏差。
Batch 内依赖: 归一化依赖于同一 batch 的其他样本,在某些任务(如生成模型、对比学习)中可能引入不希望的依赖关系。
代码实现:
import torch
import torch.nn as nn
import numpy as npclass MyBatchNorm2d:def __init__(self, num_features, eps=1e-5, momentum=0.1):"""手动实现BatchNorm2d参数:num_features: 输入特征图的通道数(C)eps: 防止除零的小常数momentum: 运行统计量的动量系数"""self.num_features = num_featuresself.eps = epsself.momentum = momentum# 可学习参数self.gamma = torch.ones(num_features) # 缩放参数self.beta = torch.zeros(num_features) # 平移参数# 运行统计量 (推理时使用)self.running_mean = torch.zeros(num_features)self.running_var = torch.ones(num_features)# 训练模式标志self.training = Truedef __call__(self, x):"""使实例可调用,直接调用forward方法"""return self.forward(x)def forward(self, x):"""前向传播输入x形状: (N, C, H, W)输出形状: (N, C, H, W)"""if x.dim() != 4:raise ValueError(f"输入应为4D张量 (N,C,H,W), 实际维度: {x.dim()}D")N, C, H, W = x.shapeif C != self.num_features:raise ValueError(f"期望通道数 {self.num_features}, 实际输入通道数 {C}")# 训练模式: 使用当前批次的统计量if self.training:# 计算每个通道的均值和方差# 在(N, H, W)维度上计算 (dim=[0,2,3])mean = x.mean(dim=(0, 2, 3)) # 形状: (C,)var = x.var(dim=(0, 2, 3), unbiased=False) # 有偏方差估计# 更新运行统计量 (指数移动平均)with torch.no_grad():self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * meanself.running_var = (1 - self.momentum) * self.running_var + self.momentum * var# 评估模式: 使用保存的运行统计量else:mean = self.running_meanvar = self.running_var# 归一化: (x - mean) / sqrt(var + eps)# 调整形状以便广播: (1, C, 1, 1)mean = mean.view(1, C, 1, 1)var = var.view(1, C, 1, 1)std = torch.sqrt(var + self.eps)# 归一化计算x_normalized = (x - mean) / std# 缩放和平移: gamma * x_normalized + beta# 调整gamma和beta形状以便广播: (1, C, 1, 1)gamma = self.gamma.view(1, C, 1, 1)beta = self.beta.view(1, C, 1, 1)out = gamma * x_normalized + beta# 保存中间结果 (反向传播需要)if self.training:self.cache = (x, mean, var, std, gamma)return outdef eval(self):"""切换到评估模式"""self.training = Falsedef train(self):"""切换到训练模式"""self.training = True# 测试代码
if __name__ == "__main__":# 设置随机种子确保结果可复现torch.manual_seed(42)np.random.seed(42)# 创建模拟输入数据 (batch_size=4, channels=3, height=32, width=32)x = torch.randn(4, 3, 32, 32)# 使用官方BatchNorm2dbn_official = nn.BatchNorm2d(3, eps=1e-5, momentum=0.1)official_output = bn_official(x)# 使用自定义BatchNorm2dbn_custom = MyBatchNorm2d(3, eps=1e-5, momentum=0.1)# 复制参数以确保公平比较with torch.no_grad():bn_custom.gamma = bn_official.weight.clone()bn_custom.beta = bn_official.bias.clone()bn_custom.running_mean = bn_official.running_mean.clone()bn_custom.running_var = bn_official.running_var.clone()custom_output = bn_custom(x) # 现在可以调用了# 比较结果print("官方BatchNorm输出形状:", official_output.shape)print("自定义BatchNorm输出形状:", custom_output.shape)# 计算差异diff = torch.abs(official_output - custom_output)print("\n最大绝对误差:", diff.max().item())print("平均绝对误差:", diff.mean().item())# 检查误差是否在可接受范围内tolerance = 1e-6assert torch.allclose(official_output, custom_output, atol=tolerance), "输出不匹配!"print("\n✅ 测试通过! 自定义实现与官方实现输出一致")# 测试评估模式bn_custom.eval()custom_eval_output = bn_custom(x)# 官方模块切换到评估模式bn_official.eval()official_eval_output = bn_official(x)# 比较评估模式结果eval_diff = torch.abs(official_eval_output - custom_eval_output)print("\n评估模式最大绝对误差:", eval_diff.max().item())print("✅ 评估模式测试通过!")2. 层归一化(Layer Normalization, LN)
核心思想: 克服 BN 对 batch size 的依赖。LN 对单个样本的所有激活值进行归一化。LN 沿着 Feature 维度 进行归一化。
操作步骤: 对于一个维度为 (B, ...) 的特征张量(可以是任意形状,常见于 (B, L, D) 序列数据或 (B, C, H, W) 图像数据):
(1)计算均值和方差: 对单个样本 b 的所有元素(忽略 Batch 维 B)计算均值和方差。
均值: (在样本 b 的所有特征维度上求平均)
方差: (在样本 b 的所有特征维度上求方差)
结果得到长度为 B 的向量 μ 和 σ²。
(2)归一化: 对样本 b 的每个元素进行归一化:
(3)缩放与偏移(仿射变换): 引入可学习的参数 γ 和 β。注意:
- 对于
(B, L, D)序列:γ和β通常是长度为D的向量(或形状(1, 1, D)的张量),应用于每个特征维度D。 - 对于
(B, C, H, W)图像:γ和β通常是长度为C的向量(或形状(1, C, 1, 1)的张量),应用于每个通道C。
训练与推理:与 BatchNorm 计算方式完全相同!LN 的归一化统计量 (μ_b, σ_b²) 仅依赖于当前单个样本,与 batch 中的其他样本无关,也与训练/推理模式无关。不需要维护全局统计量。
优点:
独立于 Batch Size: 在 batch size = 1 时也能完美工作,非常适合在线学习、大模型训练(batch size 可能很小)以及序列模型(RNN, Transformer)。
训练与推理一致: 计算逻辑完全相同,没有模式切换问题。
适合序列数据: 天然适配 RNN 和 Transformer 结构,每个时间步或 token 的处理独立于 batch 内其他序列。
样本间独立: 归一化不依赖同 batch 的其他样本,在某些任务中是优点。
缺点/局限性:
在 CNN 中效果通常不如 BN: 对于卷积特征图,直接在所有通道和空间位置 (
C, H, W) 上计算均值和方差,会模糊通道间的差异(不同通道可能代表不同特征)。而 BN 保持通道独立性。正则化效果较弱: 由于归一化仅依赖单个样本,缺乏 BN 那种由 batch 内样本多样性带来的正则化效果。
特征维度敏感: 当特征维度
D(或C * H * W)非常大时,计算出的均值和方差可能过于“全局”,忽略了特征内部的差异性。
代码实现:
import torch
import torch.nn as nn
import numpy as npclass MyLayerNorm:def __init__(self, normalized_shape, eps=1e-5):"""手动实现LayerNorm层参数:normalized_shape: 需要标准化的形状(整数或元组)eps: 防止除零的小常数"""if isinstance(normalized_shape, int):normalized_shape = (normalized_shape,)self.normalized_shape = tuple(normalized_shape)self.eps = eps# 初始化可学习参数self.weight = torch.ones(*self.normalized_shape) # gamma (缩放参数)self.bias = torch.zeros(*self.normalized_shape) # beta (平移参数)def __call__(self, x):return self.forward(x)def forward(self, x):"""前向传播输入x: 任意维度的张量,但最后 len(normalized_shape) 个维度必须匹配 normalized_shape"""# 检查输入维度是否匹配if x.size()[-len(self.normalized_shape):] != self.normalized_shape:raise ValueError(f"输入形状的最后 {len(self.normalized_shape)} 个维度必须是 {self.normalized_shape},"f"实际为 {x.size()[-len(self.normalized_shape):]}")# 计算均值和方差# 在需要标准化的维度上计算dims = tuple(range(-len(self.normalized_shape), 0))mean = x.mean(dim=dims, keepdim=True)var = x.var(dim=dims, keepdim=True, unbiased=False)# 归一化计算x_normalized = (x - mean) / torch.sqrt(var + self.eps)# 应用缩放和平移return self.weight * x_normalized + self.bias# 测试代码
if __name__ == "__main__":# 测试1: 全连接层后的LayerNorm (2D输入)print("===== 测试1: 全连接层后的LayerNorm (2D输入) =====")input_2d = torch.randn(4, 16) # (batch_size, features)# 官方实现ln_official_2d = nn.LayerNorm(16)official_output_2d = ln_official_2d(input_2d)# 自定义实现ln_custom_2d = MyLayerNorm(16)ln_custom_2d.weight = ln_official_2d.weight.data.clone()ln_custom_2d.bias = ln_official_2d.bias.data.clone()custom_output_2d = ln_custom_2d(input_2d)# 比较结果diff_2d = torch.abs(official_output_2d - custom_output_2d)print(f"最大绝对误差: {diff_2d.max().item():.6f}")print(f"平均绝对误差: {diff_2d.mean().item():.6f}")# 检查是否一致assert torch.allclose(official_output_2d, custom_output_2d, atol=1e-6), "2D输入测试失败!"print("✅ 2D输入测试通过!")# 测试2: 卷积层后的LayerNorm (4D输入)print("\n===== 测试2: 卷积层后的LayerNorm (4D输入) =====")input_4d = torch.randn(4, 3, 32, 32) # (batch_size, channels, height, width)# 官方实现 - 对整个通道+空间维度归一化ln_official_4d = nn.LayerNorm([3, 32, 32])official_output_4d = ln_official_4d(input_4d)# 自定义实现ln_custom_4d = MyLayerNorm([3, 32, 32])ln_custom_4d.weight = ln_official_4d.weight.data.clone()ln_custom_4d.bias = ln_official_4d.bias.data.clone()custom_output_4d = ln_custom_4d(input_4d)# 比较结果diff_4d = torch.abs(official_output_4d - custom_output_4d)print(f"最大绝对误差: {diff_4d.max().item():.6f}")print(f"平均绝对误差: {diff_4d.mean().item():.6f}")# 检查是否一致assert torch.allclose(official_output_4d, custom_output_4d, atol=1e-6), "4D输入测试失败!"print("✅ 4D输入测试通过!")print("\n所有测试通过!")关键对比总结
| 特性 | 批归一化 (BatchNorm, BN) | 层归一化 (LayerNorm, LN) |
|---|---|---|
| 归一化维度 | Batch 维度 (N) | Feature 维度 (通常是 C/H/W 或 D) |
| 统计量计算 | 同一通道,跨 Batch + 空间位置 (H, W) | 同一样本,跨所有特征维度 (C, H, W 或 D) |
| Batch Size 依赖 | 强依赖,小 batch 效果差/不稳定 | 无依赖,适应 batch size = 1 |
| 训练/推理差异 | 有 (训练用 batch stats, 推理用 running stats) | 无,计算方式一致 |
| 适用网络结构 | CNN (完美契合卷积层输出) | RNN, Transformer (完美契合序列数据) |
| 正则化效果 | 较强 (依赖 batch 内样本多样性) | 较弱 (仅依赖单样本) |
| 主要优点 | 加速 CNN 收敛,减少初始化依赖,正则化 | 适应任意 batch size,训练/推理一致,序列友好 |
| 主要缺点 | 小 batch size 问题,不适合 RNN/Transformer | CNN 效果通常不如 BN,正则化弱 |
| 典型输入张量形状 | (B, C, H, W) (CNN 特征图) | (B, L, D) (序列) 或 (B, C, H, W) |
| 可学习参数 γ, β | 每个通道一组 (C) | 每个特征维度一组 (C 或 D,视应用而定) |
| 计算均/方差示例 | μ_c = mean(X[:, c, :, :]) | μ_b = mean(X[b, :, :, :]) (图像) 或 μ_b = mean(X[b, :, :]) (序列) |
如何选择 BN 还是 LN?
卷积神经网络(CNN):
首选 BatchNorm: 在图像分类、目标检测、语义分割等 CNN 主导的任务中,BN 通常是默认且效果最佳的选择,尤其是在 batch size 足够大(如 >= 32)的情况下。
考虑 LN 的情况:
当 batch size 必须非常小(如 1, 2, 4)时,BN 失效,可尝试 LN。
在生成模型(如 GAN)中,有时 LN 或 InstanceNorm 效果更好。
某些轻量级 CNN 架构为了简化部署(避免维护 running stats)可能采用 LN。
循环神经网络(RNN)/ Transformer:
首选 LayerNorm: 这是 RNN 和 Transformer 架构的标准配置。Transformer 的每个子层(自注意力、FFN)后面通常紧跟着 LN (
Add & Norm)。LN 解决了变长序列和 batch size 依赖的问题。
混合架构:
如果一个模型同时包含 CNN 和 RNN/Transformer 部分(例如,CNN 作为特征提取器,后面接 RNN 或 Transformer 处理序列),通常会在 CNN 部分使用 BN,在 RNN/Transformer 部分使用 LN。
变种与扩展
Instance Normalization (IN): 对每个样本的每个通道单独归一化(计算
(H, W)上的均值和方差)。主要用于风格迁移等任务,去除图像内容对风格的依赖。Group Normalization (GN): 将通道分成若干组,在每个样本的每组通道上计算均值和方差。是 BN 在小 batch size 下的有效替代方案,常用于目标检测、分割(如 Mask R-CNN)。
Weight Normalization (WN): 直接对网络层的权重向量进行归一化,而不是对激活值。与 BN/LN 正交,有时结合使用。
Synchronized BatchNorm (SyncBN): 在多 GPU 分布式训练中,跨所有 GPU 的样本计算全局均值和方差,解决单卡 batch size 过小的问题。
总结
BatchNorm (BN) 是 CNN 的基石,通过利用 mini-batch 统计量归一化激活值,极大地加速了训练并提升了性能,但对 batch size 敏感。
LayerNorm (LN) 是 RNN 和 Transformer 的标准配置,通过基于单个样本进行归一化,完美适应了序列模型和任意 batch size 的场景,但在 CNN 中效果通常逊于 BN。
理解 BN 和 LN 的本质区别——归一化计算的维度不同(BN 沿着 Batch 维,LN 沿着 Feature 维)——是掌握它们适用场景的关键。选择哪种归一化层取决于具体的网络架构、任务类型和训练约束(尤其是 batch size)。
