当前位置：首页 > news >正文

【Reinforcement Learning】强化学习常用算法

news 2025/7/18 19:47:10

本篇只介绍QLeaning相关算法。

强化学习算法体系

1. Q-Learning

QLearning是强化学习算法中基于价值（value-based）的学习算法，它不去学习一个policy，而是学习一个Critic，该Critic不采取行为而是评价一个行为有多好或者多不好。Q-Learning通过学习一个状态-动作值函数（Q函数）来预测采取某个动作在某个状态下的期望回报。

Q即为Q(s,a)，就是在某一时刻的s状态下采取动作a动作能够获得收益的期望，环境会根据agent的动作反馈相应的回报reward，所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值，Q-table以矩阵的方式建立了一张存储每个状态下所有动作值的表格，然后根据Q值来选取能够获得最大的收益的动作。

QLearning的核心是Q-table，Q-table只是一个简单查找表的奇特名称。我们使用Q表来存储每一个状态 state，和在这个state每个行为action所拥有的Q值，Q-table的行和列分别表示state和action的值（行=状态、列=动作）。

Q-table的值Q(s,a)衡量当前state采取action到底有多好。每个Q-table的得分是机器人在该状态下采取该行动时将获得的最大预期未来奖励。这是一个迭代过程，因为我们需要在每次迭代时改进Q-Table。Q-Learning算法可以学习出Q表的每个值。

Qlearning使用了时间差分法TD（融合了蒙特卡洛和动态规划）进行离线学习, 在实际的训练过程中，通常使用贝尔曼方程来更新Q-table：

Q(s,a)表示当前状态s采取动作a后的即时奖励r，加上折价γ后的最大reward max(Q(s′,a′)。

QLearning的两个重要术语：状态-state、行为-action。QLearning的目标是达到reward值最大的state。

QLearning算法的转移规则：

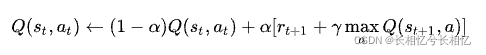
$\LARGE Q(s,a) = R(s,a)+\gamma *\underset{\widetilde{a}}{max}\left \{ Q(\widetilde{s},\widetilde{a}) \right \}$

其中，（s,a）表示当前的状态和行为，（ $\widetilde{s}$ , $\widetilde{a}$ ）表示s的下一个状态及行为，学习参数 $\gamma$ 为0-1之间的常数。这里， $\gamma$ 趋向0表示agent主要考虑“眼前奖励”，趋向1表示agent主要考虑“记忆中的奖励”。Q为待构建的矩阵，表示agent已经学到的知识，R是reward矩阵，行表示状态，列表示行为。Q与R矩阵同阶。

将agent的每一次探索称为一个episode，在每一个episode中，agent从任意初始状态到达目标状态，当agent到达目标状态后，一个episode结束，进入下一个episode。

Q-learning算法流程

建立一个Q-Table来保存状态s和将会采取的所有动作a，Q(s,a)。在每个回合中，先随机初始化第一个状态，再对回合中的每一步都先从Q Table中使用ϵ−贪婪基于当前状态 s （如果Q表没有该状态就创建s-a的行，且初始为全0）选择动作 a，执行a，然后得到新的状态s’和当前奖励r，同时更新表中Q(s,a)的值，继续循环到终点。整个算法就是一直不断更新 Q table 里的值，再根据更新值来判断要在某个 state 采取怎样的 action最好。

在这里插入图片描述

Agent通过上述Q-learning算法在经验中学习，每个episode相当于一个training session。在一个training session中，agent探索外界环境，并接收外界环境的reward，直到达到目标状态。训练的目标是要强化Q矩阵，训练的越多，Q矩阵被优化的越好。（Q被初始化为一个全0矩阵）

Q-Learnig的思想就是，如上图从上到下，先基于当前状态S，使用ϵ−贪婪法按一定概率选择动作A，然后得到奖励R，并更新进入新状态S′。此时，如果是SARSA，会继续基于状态S′，用𝜖−贪婪法选择A′,然后来更新价值函数。对于Q-Learning，基于状态S′，没有使用𝜖−贪婪法选择A′，直接使用贪婪法从所有的动作中选择最优的A′（即离线选择，不是用同样的ϵ−贪婪）。而是使用贪婪法选择A′，也就是说，选择使𝑄(𝑆′,𝑎)最大的a作为A′来更新价值函数。

Q-learning参考文献

【博客园】强化学习（七）时序差分离线控制算法Q-Learning - 刘建平Pinard

【一个教程】An introduction to Q-Learning: reinforcement learning

【CSDN】A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)

【CSDN】Q-Learning算法详解_qlearning算法详解

【CSDN】强化学习（Q-Learning，Sarsa）_强化学习 sarsa

【哔哩哔哩】李宏毅强化学习课程 (完整版) - 6

2. Deep Q Network（DQN）

dqn.pdf

DQN其实就是Deep Q-Learning算法，其算法的基本思路来源于Q-Learning，是一种Q-Learning和深度学习相结合的一种算法。Q-Learning是一种无模型的强化学习算法，它通过学习一个状态-动作值函数（Q函数）来预测采取某个动作在某个状态下的期望回报。Q-Learning算法对每个状态下的所有动作维护Q值，只能处理具有离散状态空间和离散动作空间的问题。同时，高维动作或状态空间所带来的计算开销也是难以承受的。依赖于神经网络强大的表达能力，DQN引入一个深度神经网络来代替Q表，利用深度神经网络来近似表示Q值函数，从而解决传统Q-Learning在面对大规模或连续状态空间时的计算困难。

DQN基于值迭代（Value Iteration）的思想，通过估计每个状态动作对的价值函数Q值来指导智能体在每个状态下选择最佳的动作。简单来说，就是通过深度学习训练，得到一个函数Q(s,a)可以根据输入状态s，得到最佳动作a。

若动作是连续（无限）的，Q网络的输入是状s和动作a，然后输出一个标量，表示在状态s下采取动作a能获得的价值。若动作是离散（有限）的，除了可以采取动作连续情况下的做法，我们还可以只将状态s输入到神经网络中，使其同时输出每一个动作的Q值。通常DQN以及Q-learning只能处理动作离散的情况，因为在Q函数的更新过程中有 $max_{a}$ 这一操作。

Q网络结构如下图所示：

引入神经网络后，问题的关键在于如何训练这个神经网络？与监督学习学习类似，也需要有训练集、标签、损失函数等？强化学习是通过智能与环境进行交互来学习的，这个交互个过程能够得到一个四元组（s,a,r,s'），分别表示状态、动作、奖励、下一个状态，这就是训练集的来源。强化学习的目标是得到一个比较好策略，具体到DQN中是需要得到一个比较合适的价值估计函数。

相比于Q-Learning，DQN做的改进：一个是使用了卷积神经网络来逼近行为值函数，一个是使用了target Q network来更新target，还有一个是使用了经验回放Experience replay。

Experience Replay

在一般的有监督学习中，假设训练数据是独立同分布的，我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降，随着学习的不断进行，每一个训练数据会被使用多次。在原来的Q-learning算法中，每一个数据只会用来更新一次Q值。为了更好地将Q-learning和深度神经网络结合，DQN算法采用了经验回放（experience replay）方法，具体做法为维护一个回放缓冲区，将每次从环境中采样得到的四元组数据（s,a,r,s'）（状态、动作、奖励、下一状态）存储到回放缓冲区中，训练Q网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以以减少数据相关性并且每一个样本可以被使用多次，十分适合深度神经网络的梯度学习。

DQN使用SGD训练Q网络，每次随机采样的数据batch从经验缓存中随机抽取。经验回放机制降低了DQN智能体采样数据之间的相关性，并通过复用数据样本提高了样本效率。经验缓存池中的transition由各种不同的策略（不同的Q函数）生成，但由于DQN算法的特性，在计算目标函数时无需做重要性采样。为什么DQN不需要进行重要性采样？后面解释。

Target Q Network

DQN算法最终更新的目标是让Q(s_t,a_t)逼近r+maxQ(s_t+1,a)，由于TD误差目标本身就包含神经网络的输出，因此在更新网络参数的同时目标也在不断地改变，这非常容易造成神经网络训练的不稳定性。为了解决这一问题，DQN便使用了目标网络（target network）的思想：既然训练过程中Q网络的不断更新会导致目标不断发生改变，不如暂时先将TD目标中的Q网络固定住。为了减少Q值预测中的偏差，DQN算法通过使用两个Q网络：分为eval网络和target网络，一个主网络（eval网络）用于预测Q值，另一个目标网络（target网络）用于计算目标Q值。在训练过程中，DQN只对eval网络的神经网络参数进行训练，target网络参数不进行训练，而是周期性地从eval网络的参数进行复制得到。

DQN算法流程

DQN算法的具体流程：

用随机参数初始化网络Q，用网络Q初始化target网络targetQ；
In each episode:
- For each time step t：
  - 给定状态 $s_{t}$ ，根据网络Q以贪婪策略选择动作 $a_{t}$ ；
  - 执行动作 $a_{t}$ 获得奖励 $r_{t}$ ，环境状态变为 $s_{t+1}$ ；
  - 将（ $s_{t}$ , $a_{t}$ , $r_{t}$ , $s_{t+1}$ ）存入经验回放池R中；
  - 从R中采样N个样本{( $s_{i}$ , $a_{i}$ , $r_{i}$ , $s_{i+1}$ ),i=1...N}，N通常为一个batch；
  - 对每个样本，用targetQ计算 $y_{i}=r_{i}+\gamma*max_{a}Q(s_{i+1},a)$ ；
  - 最小化目标损失 $L=\frac{1}{N}\sum_{i}(y_{i}-Q(s_{i},a_{i}))^{2}$ ，并更新当前网络Q；
  - 每C-steps更新目标网络targetQ=Q。
- end for
end for

初始化当前网络Q(s,a;θ)和目标网络Q(s,a;θ^-): θ^- ← θ
初始化回放记忆库D
初始化ε（探索率）for 每个训练周期 do初始化环境,得到初始状态sfor 每个时间步t do根据ε-贪心策略选择行动a:以概率ε随机选择a;以概率1-ε选择a=argmax_a Q(s,a;θ);执行行动a,得到奖励r和下一个状态s'将经验⟨s,a,r,s'⟩存入Ds ← s'如果D中的经验数量超过预设的mini-batch大小,then从D中随机采样一个mini-batch的经验for 每个经验⟨s,a,r,s'⟩in mini-batch doif s'是终止状态,theny ← relsey ← r + γ * max_{a'} Q(s',a';θ^-)end if计算损失 L ← (y - Q(s,a;θ))^2使用梯度下降法更新 θend forend if每隔一定的时间间隔: θ^- ← θend for
end for

DQN参考文献

【知乎】DQN从入门到放弃5 深度解读DQN算法

【博客园】强化学习（八）价值函数的近似表示与Deep Q-Learning - 刘建平Pinard

【博客园】强化学习（二）DQN算法 - Monster_bird

【动手强化学习】DQN 算法

【腾讯云开发者社区】强化学习算法解析：深度 Q 网络（Deep Q - Network，DQN）

3. Double DQN

double dqn.pdf

DoubleDQN的引入：DQN使用的是“最大值”max操作来选择动作并估计未来的价值，这种方式可能导致过高估计。其根本原因在于：

同一个网络（目标网络）既负责选择动作（动作选择偏好），又负责评估这些动作的价值（动作的价值计算）。
神经网络的逼近误差会放大估计值，从而进一步加剧过估计问题。

这种偏差会导致：

策略变得过于激进；
学习过程变得不稳定；
收敛速度减慢甚至无法收敛。

Double Q-Learning是一种用于减少过估计问题的经典方法。其基本思想是分离动作选择和价值估计。它使用两个独立的Q值表：一个表用于选择动作，另一个表用于计算目标值。通过这种分离计算，动作选择的误差不会直接影响到目标值计算，从而减少了过估计的风险。

解决target太大的问题，DoubleDQN使用两个Q-function：选择action的Q-function和计算value的Q-function不同。两个Q网络Q&Q'：

Q决定哪一个action的q_value最大；（在线网络Q用来选择动作）
Q'去计算新的q_value。（目标网络Q'用来计算目标Q值）

这样，DDQN通过解耦目标Q值动作的选择和目标Q值的计算这两步，来解决“过估计”的问题。

传统DQN的目标值：

maxQ操作可以拆分为两步：首先基于Q值判断状态s'下的最优动作，然后计算最优动作的Q值。

DDQN的目标值改为：

DDQN更新过程

state下，使用Q网络计算action的Q值，q_value=Q(s,a)；
next_state下，使用Q网络选择Q值最大的action，argmax_aQ(s',a)；
使用targetQ网络来估计这个action并输出Q值：next_q_value=Q'(s',a)；
目标Q值：q_target=reward+r*next_q_value；
计算loss：loss=MSE(q_value,q_target)。

DQN与DDQN对比

在传统的DQN算法中，本来就存在两套神经网络：目标网络和训练网络，只不过的计算 $max_{a}Q(s_{i+1},a)$ 时只用到了其中的目标网络。因此我们恰好可以直接将训练网络Q作为Double DQN算法中的第一套神经网络来选取动作，将目标网络targetQ作为第二套神经网络计算Q值，这便是DoubleDQN的主要思想。

DQN：使用targetQ网络来选择动作和估计Q值，targetQ既选择动作又评估Q值。
DDQN：使用Q网络来选择动作同时使用targetQ网络来计算Q值。

很显然，DQN与DoubleDQN的差别只是在于计算状态s'下Q值时如何选取动作，所以DoubleDQN 的代码实现可以直接在DQN的基础上进行，无须做过多修改。

# DQN与DDQN对比伪代码
q_values = Q(states,actions);
if "doubleDQN":max_action = Q(next_states).max; # s'使用Q网络选择Q值最大的actionmax_next_q_values = targetQ(next_states,max_action);
else:max_next_q_values = targetQ(next_states).max
q_target = reward+r*max_next_q_values;
loss = MSE(q_values,q_target);

q_values = self.q_net(states).gather(1, actions)  # Q值
# 下个状态的最大Q值
if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别max_action = self.q_net(next_states).max(1)[1].view(-1, 1)max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
else: # DQN的情况max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)  # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数

DDQN参考文献

【腾讯云开发者社区】强化学习-Double DQN(Double Deep Q-Network)算法

【动手强化学习】DQN 改进算法

4. Dueling DQN

dueling dqn.pdf

DuelingDQN是DQN的另一种的改进算法，它在传统DQN的基础上只进行了微小的改动，但却能大幅提升DQN的表现。DuelingDQN算法对于普通DQN算法的改进体现在Q值网络的结构上（二者仅网络结构不同），DuelingDQN只改变了网络的最后一层，在DuelingDQN中的Q值网络具有如下结构：

上面的结构为普通的DQN网络，其输出为每个action的Q值，未区分状态价值和动作价值。

下面的结构为DuelingDQN网络，DuelingDQN将Q网络分成两部分：第一部分仅与状态s有关和动作a无关，第二部分同时与状态s和动作a有关。DuelingDQN通过将Q值的计算过程拆分为两个分支：一个是状态价值函数（state value function），另一个是动作优势函数（advantage function），这两个函数分别估计了在给定状态下采取任何动作的预期回报和特定动作相对于平均回报的优势，以此来更精确地估计Q值。

状态价值函数V(s)：表示在某个状态下，不考虑任何特定动作的总体价值，即该状态的整体价值。
优势函数A(s,a)：表示在给定状态下，选择特定动作相比其他动作的优势，即该动作相对于平均的优越程度。
状态动作价值函数Q减去状态价值函数V的结果定义为优势函数A：A(s,a)=Q(s,a)-V(s)。
状态值函数V(s)可以理解为：在该状态下所有可能动作所对应的动作值函数乘以采取该动作的概率的和。更通俗的讲，值函数V(s)是该状态下所有动作值函数关于动作概率的平均值。
动作值函数Q(s,a)是单个动作所对应的值函数。
优势函数Q_π(s,a)：能评价当前动作值函数相对于平均值的大小。所以，这里的优势指的是动作值函数相比于当前状态的值函数的优势。如果优势函数大于零，则说明该动作比平均动作好，如果优势函数小于零，则说明当前动作还不如平均动作好。

DuelingDQN分别估计状态价值函数和动作价值函数的原因是，在某些状态下，V函数的值估计比Q函数的值估计更有意义（部分状态下不是所有动作的Q值函数都值得精确估计），此时将二者分开能够使智能体更好地处理与动作关联较小的状态，这样的学习过程更加稳健。

另一个优势是DuelingDQN能够更高效地学习V值函数。每当V值函数更新时，除了采样动作外的其他动作的Q值也会被更新，这样的学习更高效且准确。而传统的DQN每次只会更新某个动作的Q值，其他动作的Q值不会更新。

网络结构解析：注意V和A是标量还是向量。

DuelingDQN参考文献

【动手强化学习】DQN 改进算法

【CSDN】强化学习：Dueling DQN 学习笔记_dueling dqn算法

5. DQN类算法对比

在传统的DQN基础上，DoubleDQN和DuelingDQN都是非常容易实现的变种。DoubleDQN解决了 DQN中对Q值的过估计问题，而DuelingDQN能够很好地学习到不同动作的差异性，在动作空间较大的环境下非常有效。

简述一下DQN、Double DQN、Dueling DQN的主要区别：

DQN算法在更新Q值时，会使用同一个targetQ网络来选择动作和计算目标Q值。这种做法会导致Q值的估计偏高，即存在一个过估计问题over estimation。DQN
Double DQN使用两套独立的神经网络缓解过估计问题：使用Q网络来选择动作，使用targetQ网络来计算目标Q值。Double DQN

Dueling DQN与DQN的网络结构不同，将DQN中的Q值函数分解为状态值函数和优势函数两个部分，Q(s,a)=V(s)+A(s,a)。DuelingDQN

# DQN VS DDQN：下一个状态的最大Q值计算逻辑不同
q_values = Q(states,actions);
if("doubleDQN"):max_action = Q(next_states).maxmax_next_q_value = targetQ(next_state,max_action)
else:max_next_q_value = targetQ(next_state).max
q_target = reward + r*max_next_q_value
loss = MSE(q_values,q_target)

5.1 为什么DQN存在过估计问题？

过估计：估计的值函数比真实的值函数大。

从Q值计算公式解释一下这个问题：

$Q(s_{t},a_{t})=r_{t}+\underset{a}{max}Q(s_{t+1},a)$

DQN的最大化操作选择和估计action使用相同的值。
DQN很容易选择被高估的action当作 $\underset{a}{max}Q(s_{t+1},a)$ 的结果来更新targetQ value。

底层逻辑还是TD算法导致DQN高估真实的动作价值：

Reason1：最大化导致高估，求最大化使得TD target大于真实值，导致DQN高估，为非均匀高估。
Reason2：用自己的估计再去估计自己，当前DQN出现高估，下一轮TD target更会高估，进一步推高DQN的输出。

Epsilon Greedy（避免局部最优）：

5.2 DQN为什么要使用两个网络？

DQN算法通常包含两个网络：一个是评估网络Q，另一个是目标网络targetQ。这两个网络的结构和初始权重是相同的，但它们的权重是不同步更新的。使用两个网络的原因是为了稳定学习过程。在DQN算法中，目标网络的权重是定期从评估网络网络复制的，但更新的频率远低于评估网络网络。这种做法有助于减少目标Q值（即预期的回报）与当前Q值（即实际的回报）之间的相关性，从而减少了学习过程中的波动性。

DQN使用Q来计算q_values，而使用targetQ计算next_q_values。

q_values:

q_values代表在当前状态下采取实际执行的动作所对应的Q值。
这些Q值是通过Q网络计算得到，因为Q网络是实时更新的，它反映了最新的策略或价值估计。
在给定的状态state_batch下，通过Q网络计算所有可能动作的Q值，然后使用gather函数根据实际采取的动作action_batch来选择对应的Q值。

next_q_values: