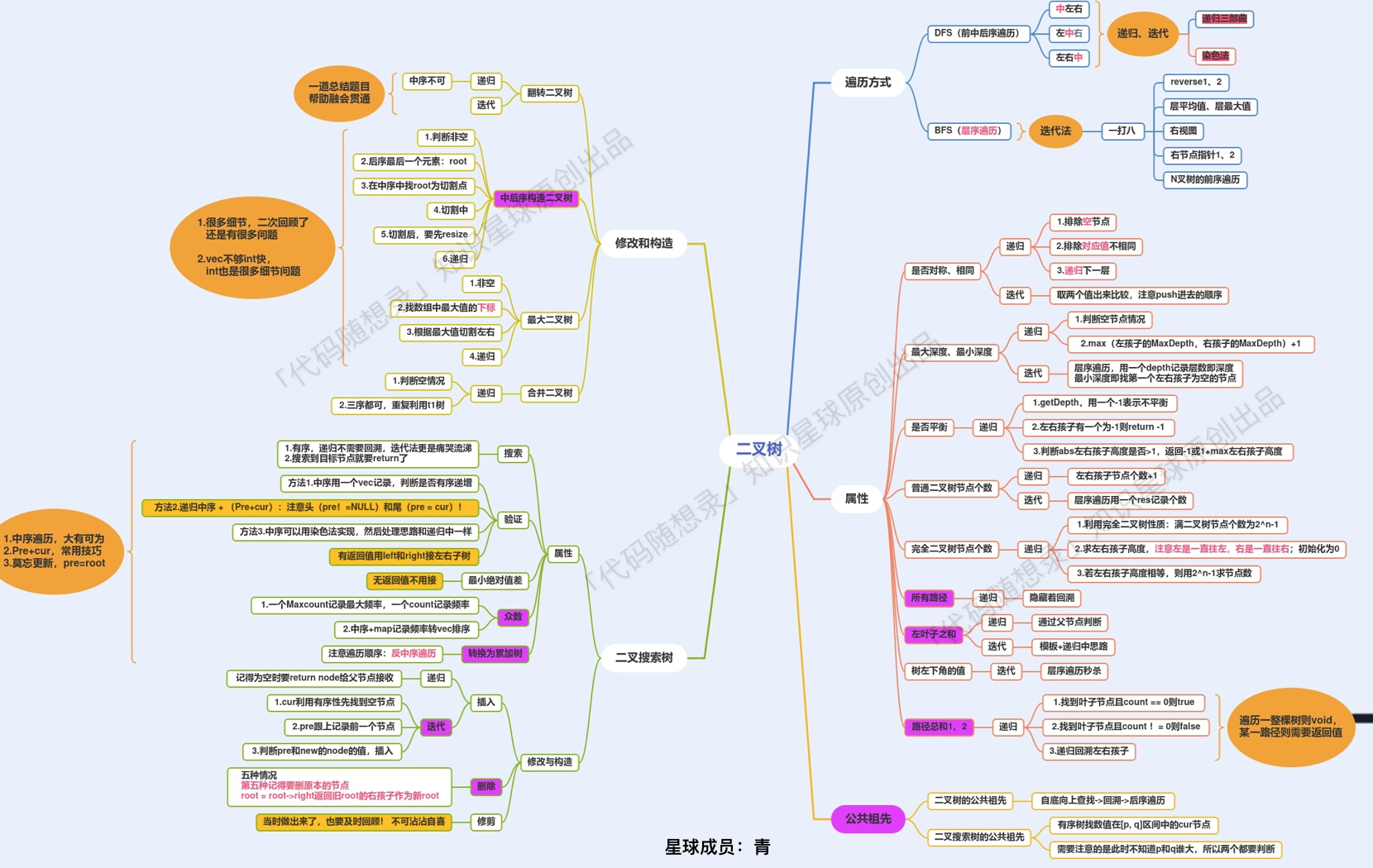
代码随想录Day21:二叉树(修剪二叉搜索树、将有序数组转换为二叉搜索树、把二叉搜索树转换为累加树——全递归版本以及总结)
一、实战
669修剪二叉搜索树
669. 修剪二叉搜索树 - 力扣(LeetCode)
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
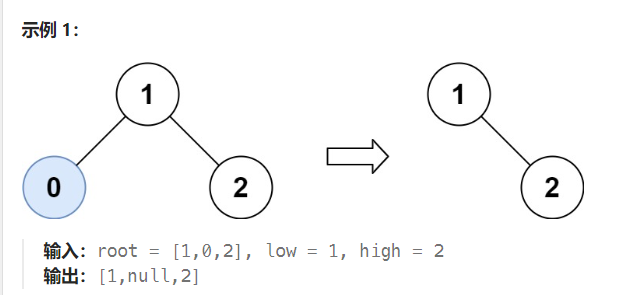
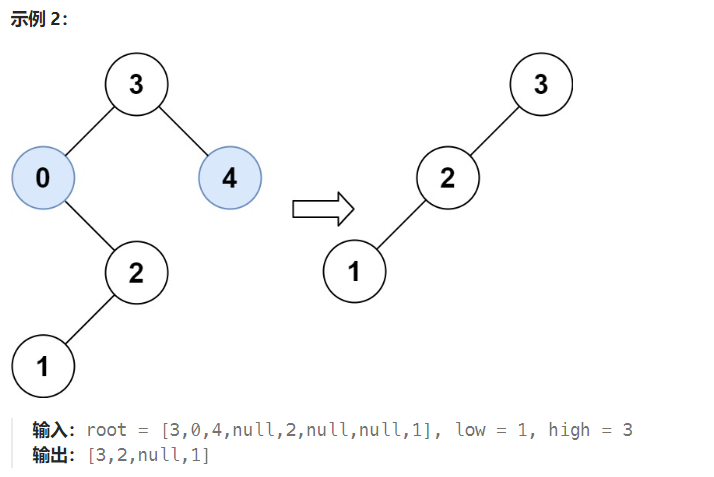
- 树中每个节点的值都是 唯一 的
思路:基础思路就是删除二叉树中的节点
错误想法:递归处理,然后遇到 root->val < low || root->val > high 的时候直接return NULL,一波修改,赶紧利落。
//C++版本错误代码,主要就是理解思路
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr || root->val < low || root->val > high) return nullptr;root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的,还要考虑节点0的右子树。过早地进行判断可能会导致不应该删除的分支被删除。
本题与删除BST节点的不同之处?通义大模型-参考
本题(修剪二叉搜索树)与删除二叉搜索树(BST)中的节点虽然都涉及到对树结构的修改,但它们的目标和操作方式有着本质的区别。以下是两者之间的主要不同点:
1. 目标不同
修剪BST:目的是将所有不在给定范围 [low, high] 内的节点从树中移除,同时保持剩余节点的相对结构不变。这意味着你可能需要移除一个节点及其一部分子树,并且这种移除可能是连续的(即一个节点被移除后,其部分或全部祖先节点也可能因为不满足条件而被移除)。
删除BST中的节点:目标是移除树中的一个特定节点,并确保在删除该节点之后,BST 的性质仍然得到保持(即对于每个节点,左子树的所有节点值小于它,右子树的所有节点值大于它)。删除操作通常涉及处理三种情况:要删除的节点没有子节点、只有一个子节点、有两个子节点。
2. 操作方式不同
修剪BST:通过递归遍历整个树来实现。如果当前节点不符合条件,则根据 BST 的性质决定是保留左子树还是右子树进行进一步的检查和修剪。这个过程可能会导致连续地“跳过”一系列节点,直到找到符合范围的节点为止。
删除BST中的节点:需要定位到特定的节点并根据它是否有子节点及子节点的数量采取不同的策略来维持 BST 的结构。例如,如果要删除的节点有两个子节点,那么通常会寻找它的前驱或后继节点(即左子树的最大值或右子树的最小值),将其值复制到要删除的节点位置,然后删除前驱或后继节点。
3. 结果的不同
修剪BST:最终结果是一个新的 BST,其中所有节点的值都在指定范围内,且原始树中未被移除节点的相对结构得到了保持。
删除BST中的节点:只影响被直接删除的那个节点以及必要的时候调整与其相关的节点(如上述提到的前驱或后继节点),其余部分的树结构基本保持不变。总结来说,尽管两个操作都涉及到改变树的结构,但它们关注的重点不同:修剪是关于范围过滤,而删除是关于精确移除某个节点并保持BST的性质。因此,两种操作的具体实现也大相径庭。
package org.example.Tree;public class trimBST669 {public TreeNode trimBST(TreeNode root, int low, int high) {TreeNode result=traversal(root,low,high);return result;}private TreeNode traversal(TreeNode root, int low, int high) {if(root==null)return null;if (root.val > high) {// 当前节点和右子树都不合法,只保留左子树继续处理return traversal(root.left, low, high);}if (root.val < low) {// 当前节点和左子树都不合法,只保留右子树继续处理return traversal(root.right, low, high);}// 当前节点合法,继续处理左右子树root.left = traversal(root.left, low, high);root.right = traversal(root.right, low, high);return root;}}
108将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/
有序数组——平衡二叉搜索树
整体思路:因为BST的性质,选取一个中间的节点,将数组分为左区间和右区间,继续遍历左区间和右区间直至终止。因此本题遍历顺序不重要,重要的是区间开闭、终止条件的确定、在遍历的同时完成构造二叉树
package org.example.Tree;public class sortedArrayToBST108 {public TreeNode sortedArrayToBST(int[] nums) {TreeNode root=traversal(nums,0,nums.length-1);return root;}//left分别为区间左边界, right右边界//注意,traversal区间都统一设置为左闭右开//left=right也需要继续构造private TreeNode traversal(int[] nums,int left,int right){if(left>right)return null;int mid=(left+right)/2;TreeNode temp=new TreeNode(nums[mid]);//left,注意左边遍历最后的结果要变为分支temp.left=traversal(nums,left,mid-1);//righttemp.right=traversal(nums,mid+1,right);return temp;}
}
538把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 - 力扣(LeetCode)
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
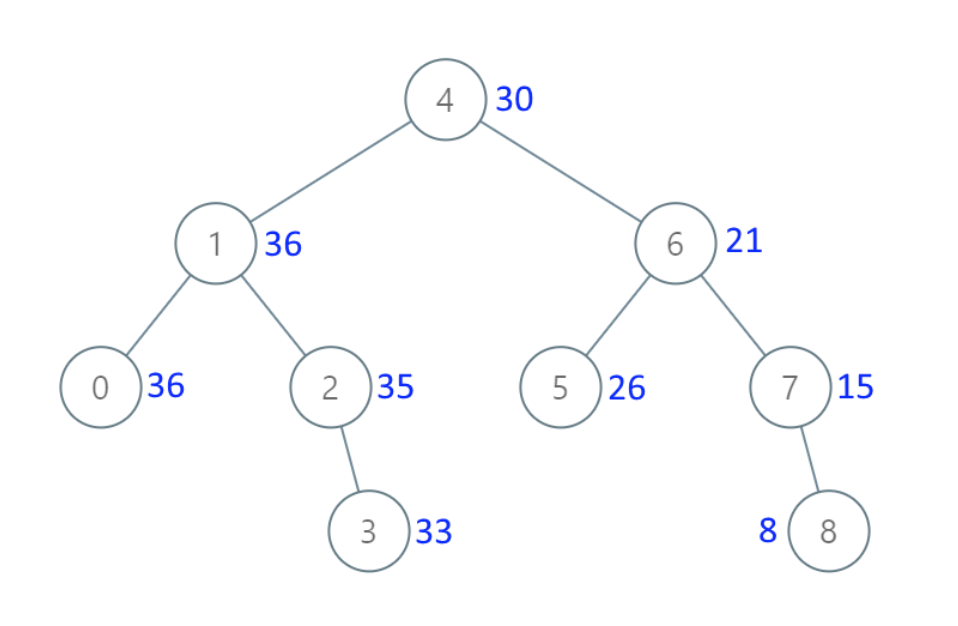
- 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
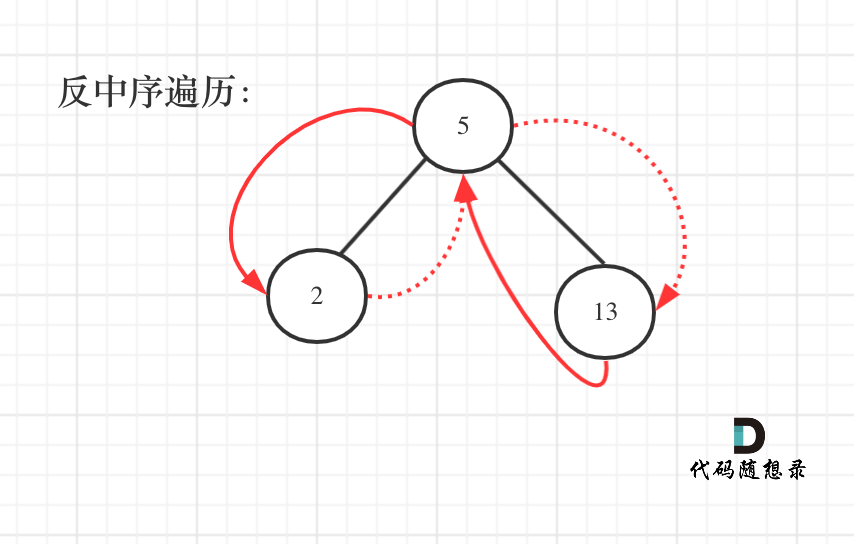
思路:根据上面蹄片我们可以总结出基础思路,也就是从右边往左边进行遍历,用双指针实现逐步叠加的效果。根据之前二叉树的基础题目,我们可以得出常规写法。
package org.example.Tree;public class convertBST538 {TreeNode pre=null;public TreeNode convertBST(TreeNode root) {traversal(root);return root;}//中序遍历变体,右-中-左private void traversal(TreeNode root) {if(root==null)return;traversal(root.right);//pre为null的话就说明是第一个节点,也就是最大的那个,不用变if(pre!=null)root.val= root.val+ pre.val;pre=root;traversal(root.left);}
}
当然,也可以将pre设置为节点的val值,这样更直观。
二、总结(全递归版本)
关于二叉树的属性
- 二叉树:是否对称(opens new window)
- 递归:后序,比较的是根节点的左子树与右子树是不是相互翻转
- 二叉树:求最大深度(opens new window)
- 递归:后序,求根节点最大高度就是最大深度,通过递归函数的返回值做计算树的高度
- 二叉树:求最小深度(opens new window)
- 递归:后序,求根节点最小高度就是最小深度,注意最小深度的定义
- 二叉树:求有多少个节点(opens new window)
- 递归:后序,通过递归函数的返回值计算节点数量
- 二叉树:是否平衡(opens new window)
- 递归:后序,注意后序求高度和前序求深度,递归过程判断高度差
- 二叉树:找所有路径(opens new window)
- 递归:前序,方便让父节点指向子节点,涉及回溯处理根节点到叶子的所有路径
- 二叉树:递归中如何隐藏着回溯(opens new window)
- 详解二叉树:找所有路径 (opens new window)中递归如何隐藏着回溯
- 二叉树:求左叶子之和(opens new window)
- 递归:后序,必须三层约束条件,才能判断是否是左叶子。
- 二叉树:求左下角的值(opens new window)
- 递归:顺序无所谓,优先左孩子搜索,同时找深度最大的叶子节点。
- 二叉树:求路径总和(opens new window)
- 递归:顺序无所谓,递归函数返回值为bool类型是为了搜索一条边,没有返回值是搜索整棵树。
关于二叉树的修改和构造
- 翻转二叉树(opens new window)
- 递归:前序,交换左右孩子
- 构造二叉树(opens new window)
- 递归:前序,重点在于找分割点,分左右区间构造
- 构造最大的二叉树(opens new window)
- 递归:前序,分割点为数组最大值,分左右区间构造
- 合并两个二叉树(opens new window)
- 递归:前序,同时操作两个树的节点,注意合并的规则
关于二叉搜索树的属性
-
二叉搜索树中的搜索(opens new window)
- 递归:二叉搜索树的递归是有方向的
-
是不是二叉搜索树(opens new window)
- 递归:中序,相当于变成了判断一个序列是不是递增的
-
求二叉搜索树的最小绝对差(opens new window)
- 递归:中序,双指针操作
-
求二叉搜索树的众数(opens new window)
- 递归:中序,清空结果集的技巧,遍历一遍便可求众数集合
-
二叉搜索树转成累加树(opens new window)
- 递归:中序,双指针操作累加
关于二叉树的公共祖先
- 二叉树的公共祖先问题(opens new window)
- 递归:后序,回溯,找到左子树出现目标值,右子树节点目标值的节点。
- 二叉搜索树的公共祖先问题(opens new window)
- 递归:顺序无所谓,如果节点的数值在目标区间就是最近公共祖先
关于二叉搜索树的修改与构造
- 二叉搜索树中的插入操作(opens new window)
- 递归:顺序无所谓,通过递归函数返回值添加节点
- 二叉搜索树中的删除操作(opens new window)
- 递归:前序,想清楚删除非叶子节点的情况
- 修剪二叉搜索树(opens new window)
- 递归:前序,通过递归函数返回值删除节点
- 构造二叉搜索树(opens new window)
- 递归:前序,数组中间节点分割
最后总结
-
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
-
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
-
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
注意:在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径也用了前序,这是为了方便让父节点指向子节点。所以求普通二叉树的属性还是要具体问题具体分析。
(图是 代码随想录知识星球成员:青,所画)