(李宏毅)deep learning(五)--learning rate
一,关于learning rate的讨论:
(1)在梯度下降的过程中,当我们发现loss的值很小的时候,这时我们可能以为gradident已经到了local min=0(低谷),但是很多时候,loss很小并不是因为已经到达了低谷,而是(如下图):
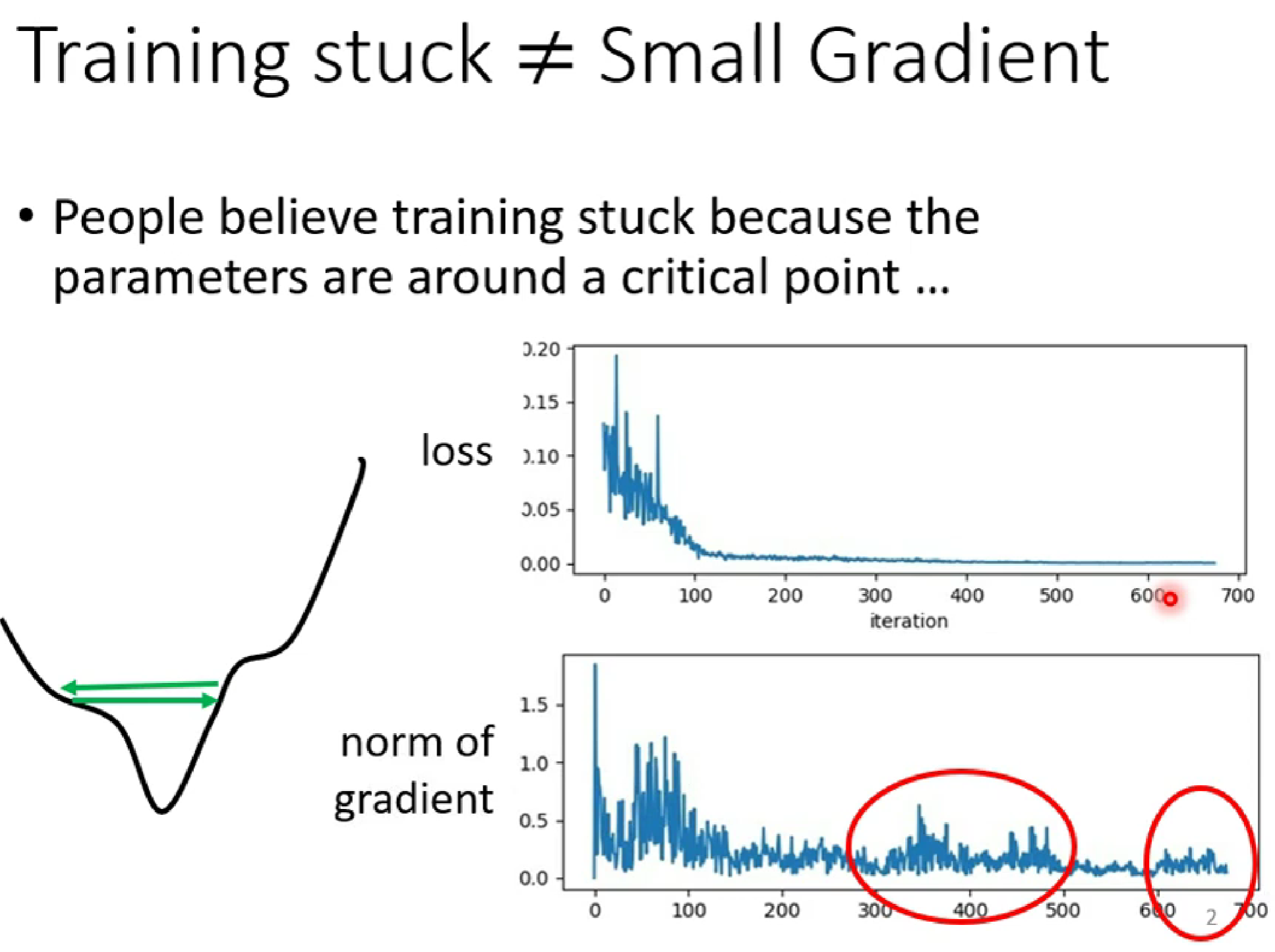
如上图,当右上角的loss几乎为0时,右下角的gradient并没有趋近于0,而是出现反复的极值 ,这种情况下是因为learning rate过大,是的变化的幅度过大,是的optimisization卡在山腰(如左下角)。
(2)然而,我们指的learning rate并不是越大越好,也不是越小越好。
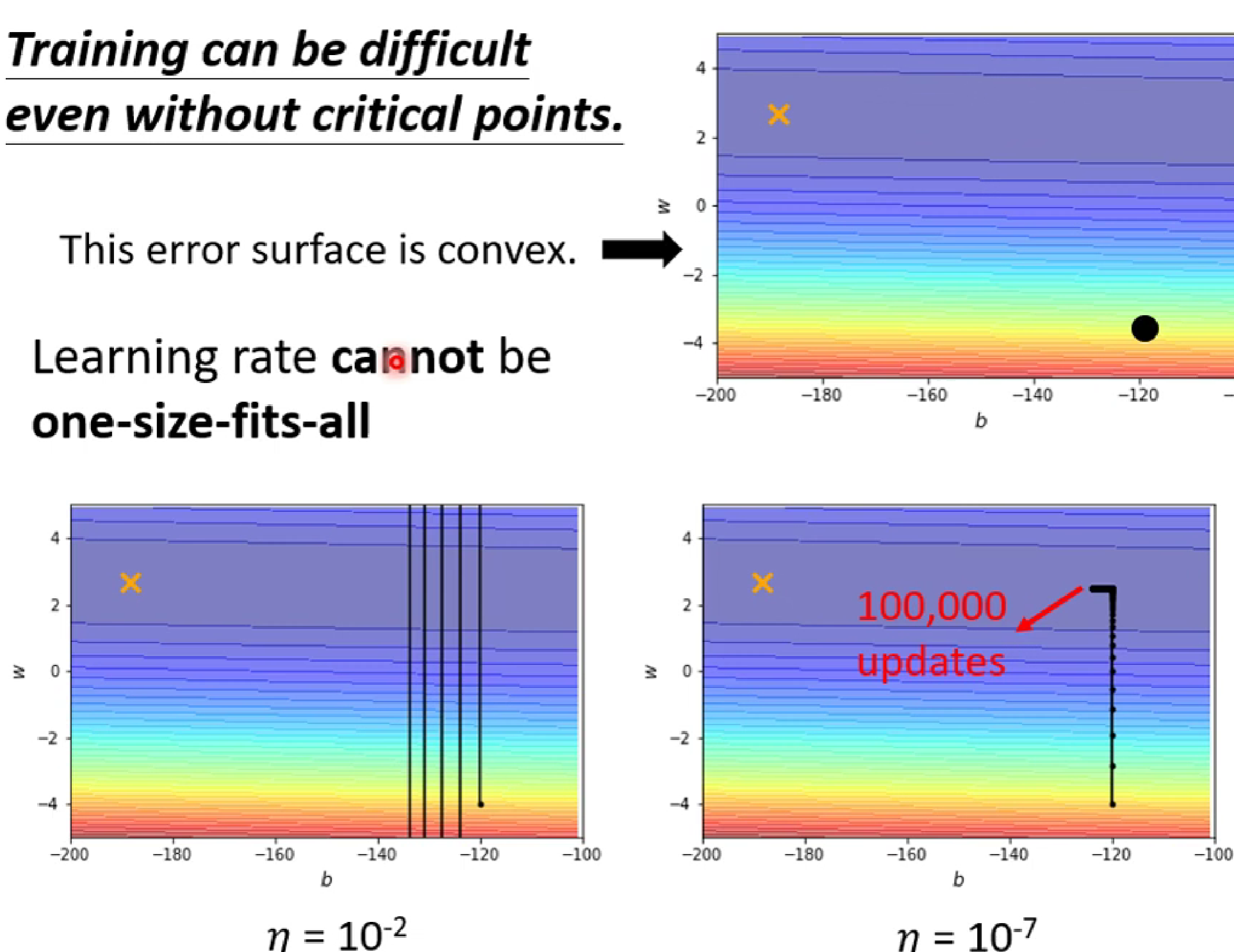
如上图左下角,因为learning rate过大,使得梯度跨度过大不能进入低谷到达黄色叉叉,而如果选择 learning rate过大,梯度移动缓慢,在进入低谷后在大updates之后还是难以到达黄色叉叉。
因为,我们需要一个自动化改变的learning rate,在坡度较陡的时候减小learning rate,在坡度较小的时候增大.
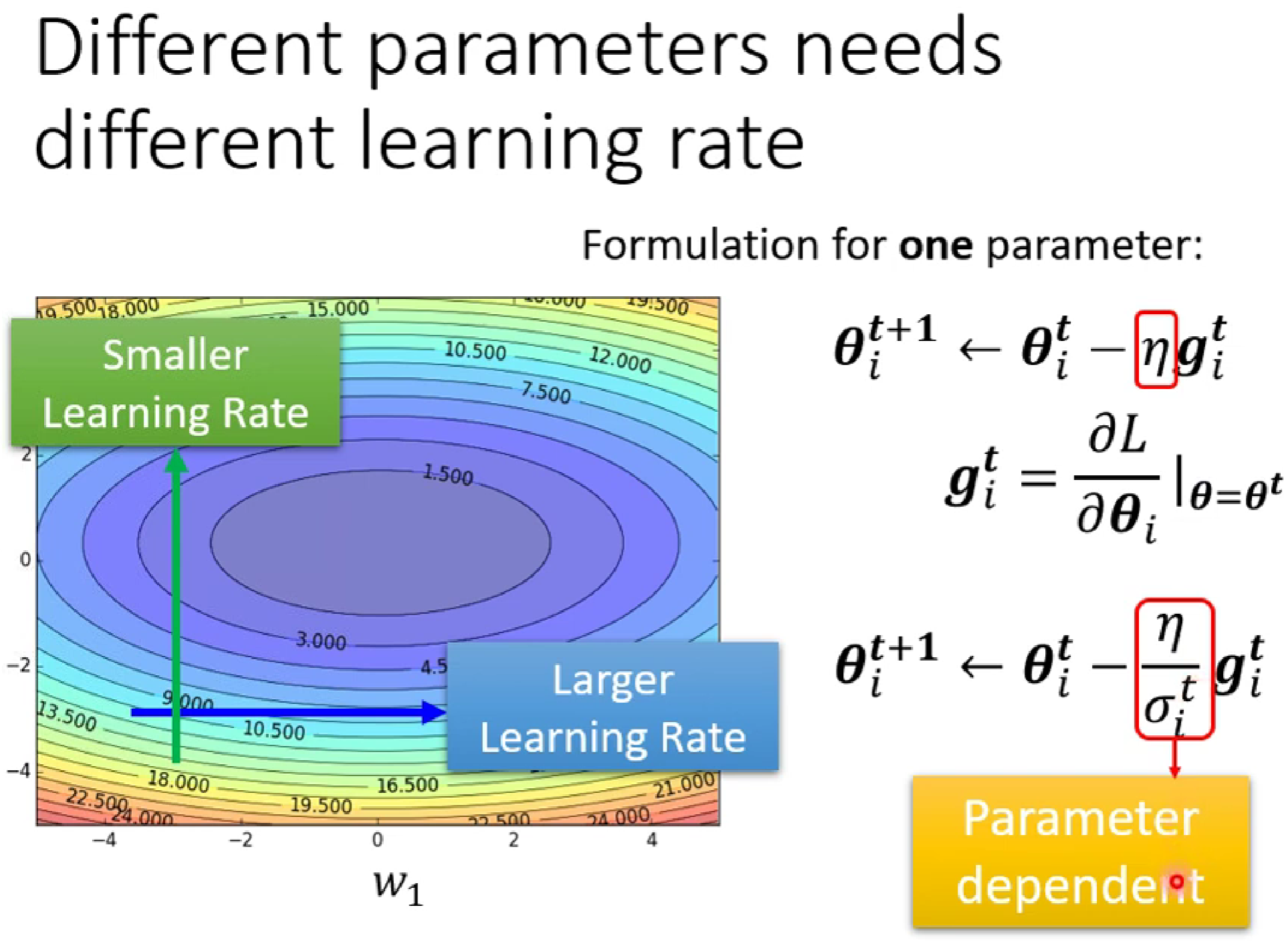
这时,我们想着在之前的learning rate 下加一个随i变化的δ。
δ的求法如下:
(第一种求法)δ是前面所有gradient绝对值的均方
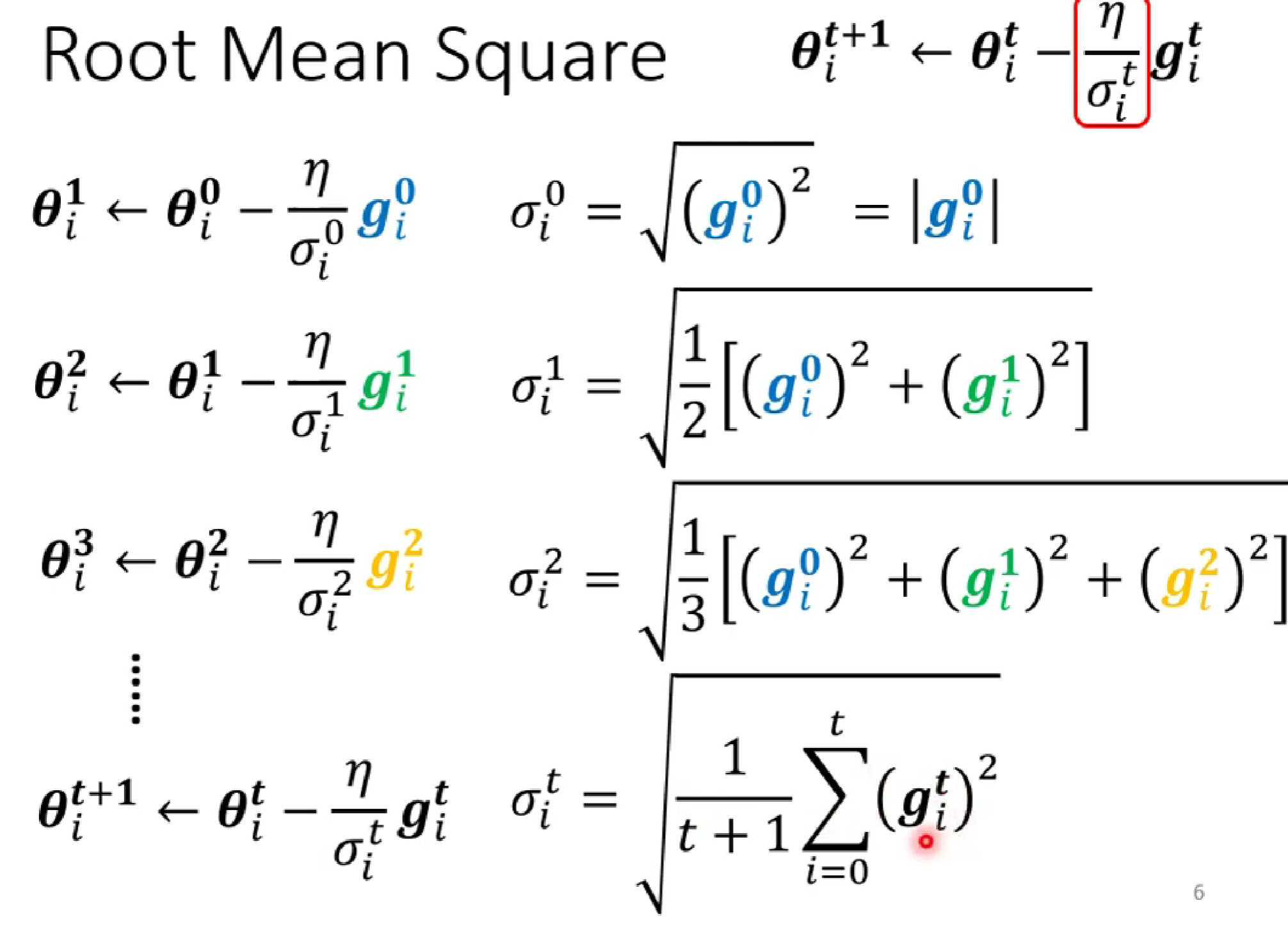
(第二种求法) :第一种的缺点是,因为是全部平均,难以在陡的地方快速减小gradident,在缓的地方减小gradident。为此,我们添加了α权重,减少之前的梯度影响,但又保留一定的惯性。
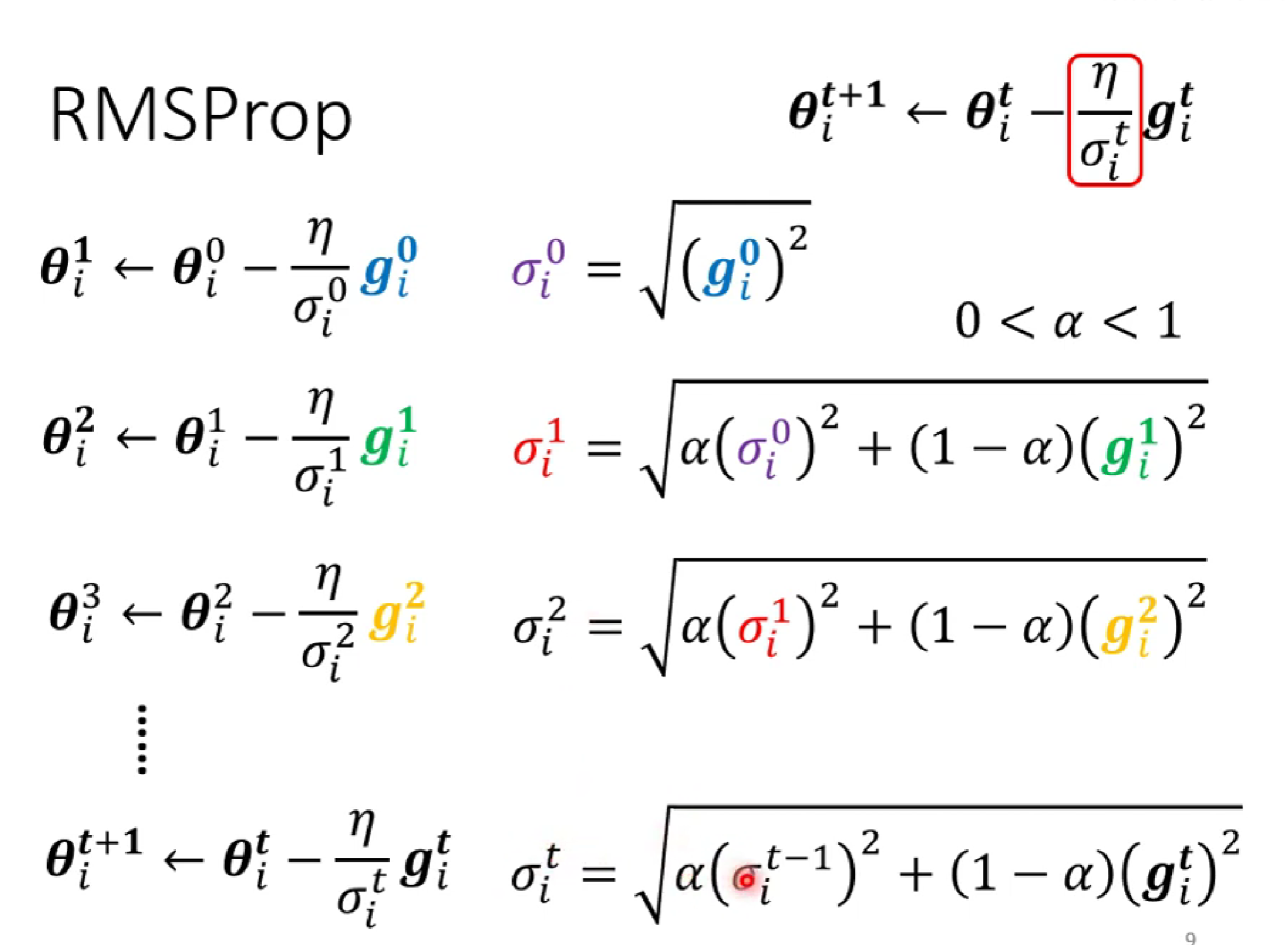
但是呢,运行后的结果会出现:
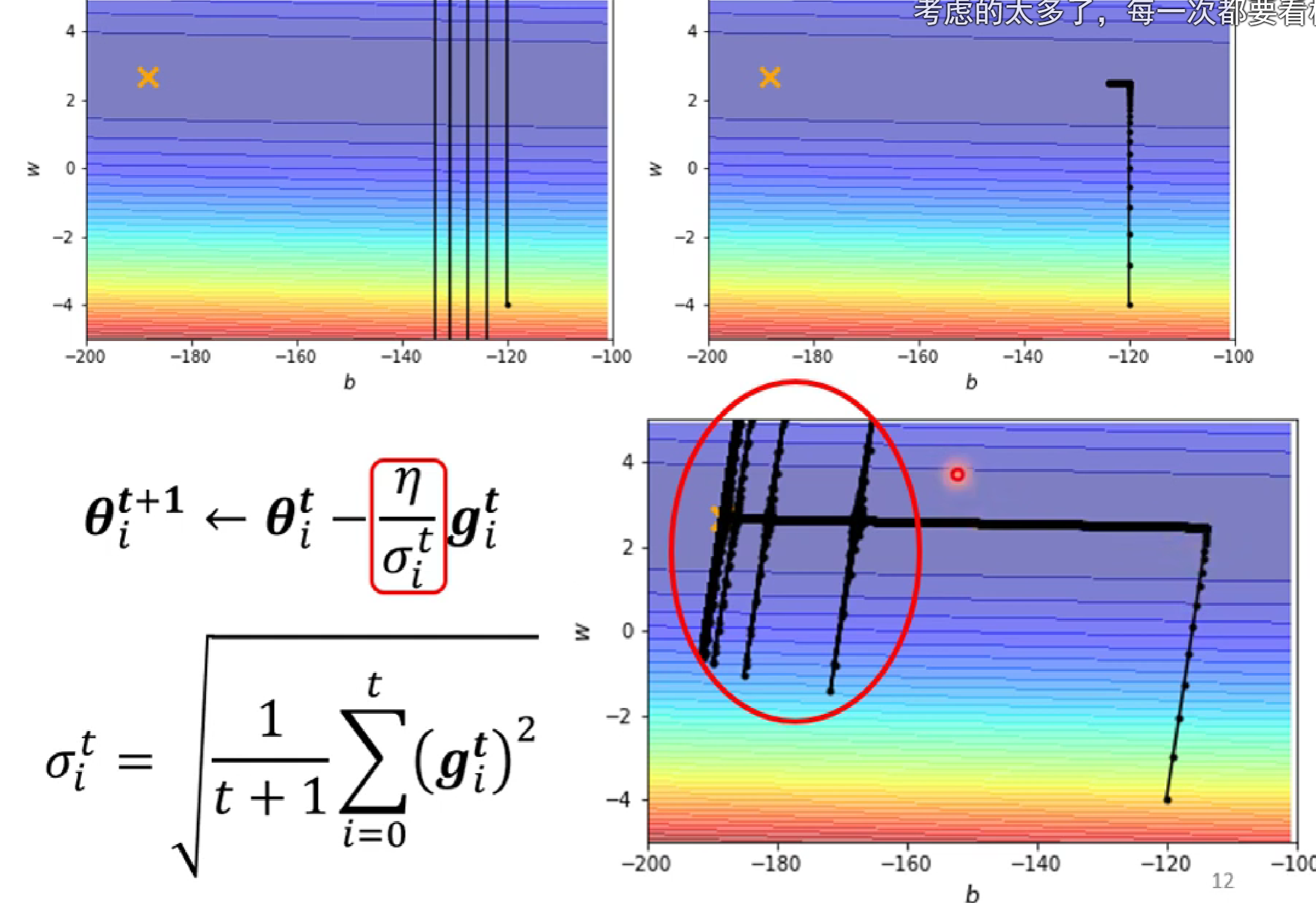
这是因为,在y轴方向,一开始较陡,δ较大,当左转进入较缓的低谷时,δ中的gardient不断增大,当前面的大gradient的和影响不断减小,由当前的δ占主导时,小δ使得y轴learning rate突然增大,发生沿y方向移动,之后由于遇上陡坡,learning rate减小而返回。
解决方法:让learning rate n也随着t减小(有点模拟退火的思维)
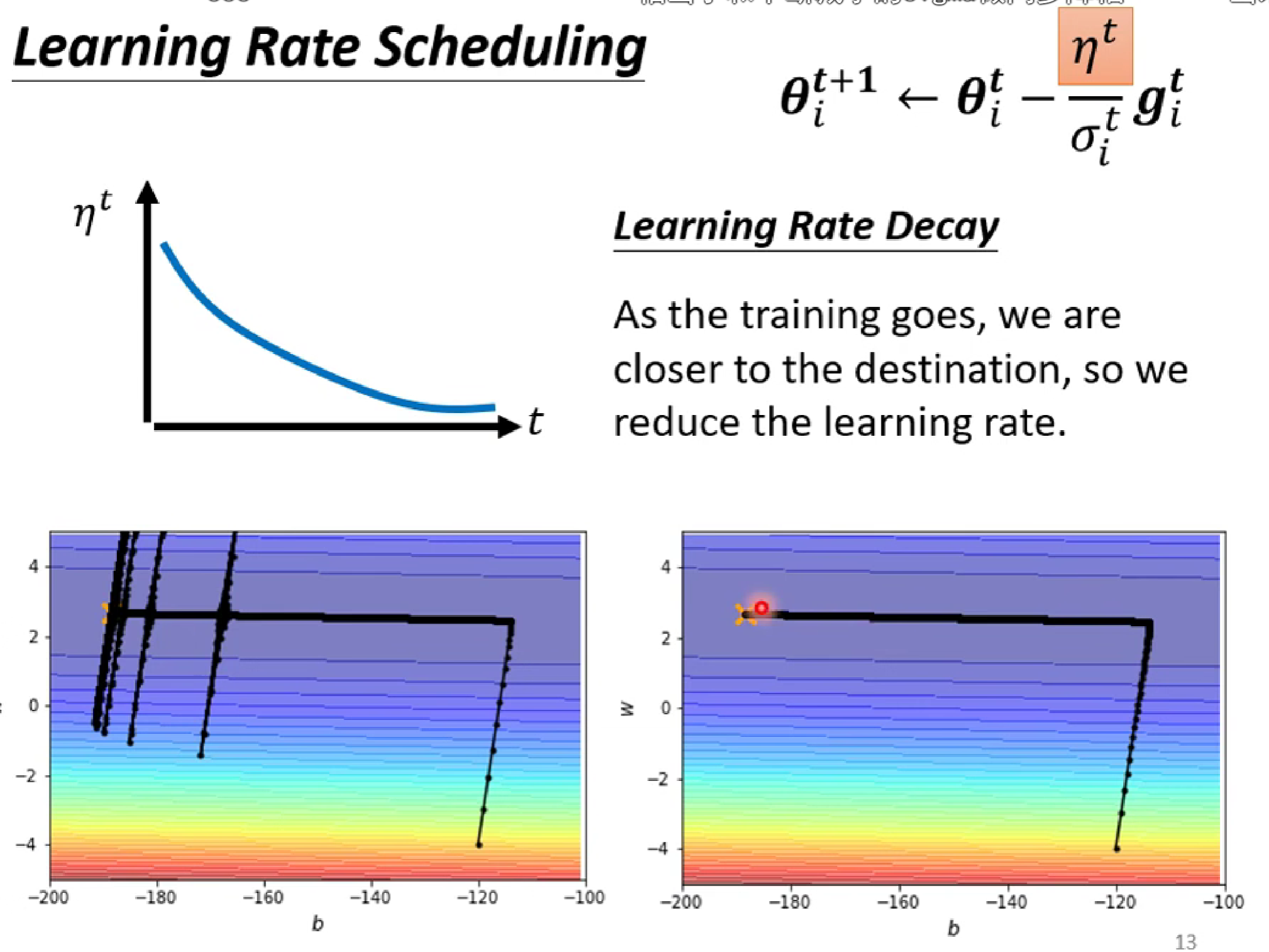
还有一个方法:进行预加热(Warm up)。
Warmup的核心思想是在训练的初始阶段,将学习率从较小的值逐步增加到预设的目标值,而不是直接使用较大的学习率。这一过程类似于“热身”,让模型在训练初期逐步适应数据分布,从而减少训练的不稳定性。

今天就学到这啦。
