当前位置：首页 > news >正文

【模板】树状数组

news 2025/8/3 18:12:52

目录：

单点修改，区间查询：

        题目描述：

        lowbit()运算：

        插入、修改单点数据：

        计算前缀和：

        完整代码：

区间修改，单点查询：

        计算差分数组：

        计算每个点的值：

        完整代码：

单点修改，区间查询：

题目描述：

如题，已知一个数列，你需要进行下面两种操作：

将某一个数加上 x
求出某区间每一个数的和

输入格式

第一行包含两个正整数 n, m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

1 x k 含义：将第 x 个数加上 k
2 x y 含义：输出区间 [x, y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

lowbit()运算：

//非负整数n在二进制表示下最低位1及其后面的0构成的数值
//eg.lowbit(12) = lowbit((1100)2) = (100)2 = 4
//将1100按位取反后加一得到0100，会发现除了最低位的一和后面的零，其余位上与原数均相反
//故两者按位与后正好得到最低位1及其后面的0构成的数值
//又取反加一为补码，故lowbit为k & -k
int lowbit(int k) {return k & -k;
}

插入、修改单点数据：

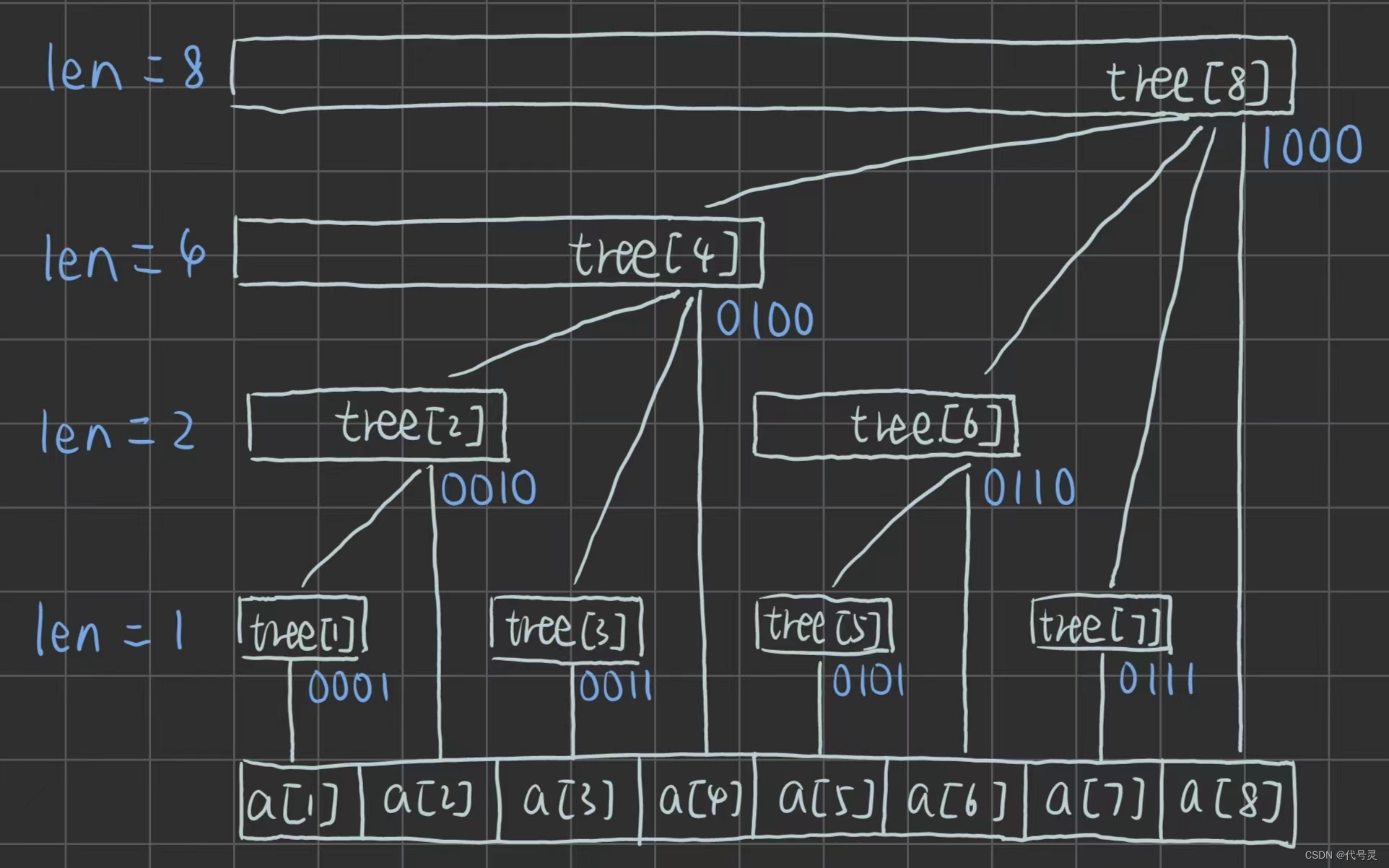
//如图：
//tree[x]保存以x为根的子树中叶节点值的和
//将x转化为二进制后，发现每一层的末尾的零的个数都相同
//且tree[x]覆盖的长度即为lowbit(x)的值
//tree[x]的父节点为tree[x + lowbit(x)]
void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}

计算前缀和：

//由图可知，若求前7项的和，则该值为tree[7] + tree[6] + tree[4]
//故，通过循环可以求出结果
int sum(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}

完整代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, a, flag, p, q, tree[N];int lowbit(int k) {return k & -k;
}void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}int sum(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}int main() {scanf("%d %d", &n, &m);for(int i = 1; i <= n; ++i) {scanf("%d", &a);add(i, a);}for(int i = 1; i <= m; ++i) {scanf("%d %d %d", &flag, &p, &q);if(flag == 1)add(p, q);elseprintf("%d\n", sum(q) - sum(p - 1));}return 0;
}

区间修改，单点查询：

计算差分数组：

//与单点修改、区间查询类似
void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}

计算每个点的值：

//与单点修改、区间查询类似
//此时计算的结果为每个点的值
int query(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}

完整代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, now, last, flag, p, q, num, tree[N];int lowbit(int k) {return k & -k;
}void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}int query(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}int main() {scanf("%d %d", &n, &m);//计算差分数组，将相差的值放入数组中//eg.原本的数组应为a[] = {1, 6, 8, 5, 10}//则差分数组应为b[] = {1, 5, 2, -3, 5}for(int i = 1; i <= n; ++i) {scanf("%d", &now);add(i, now - last);last = now;}for(int i = 1; i <= m; ++i) {scanf("%d", &flag);//若要修改区间[p, q]的值//例如上述举的例子，若要将区间[2, 4]均加上3//则原数组变为a[] = {1, 9, 11, 8, 10}//差分数组变为b[] = {1, 8, 2, -3, 2}//即对差分数组来说只需修改下标为p的值，和下标为q + 1的值if(flag == 1) {scanf("%d %d %d", &p, &q, &num);add(p, num);add(q + 1, -num);}//若查询某个点的值//前p个差分数组的值相加即为该点的值//与单点修改、区间查询中的求前缀和类似else {scanf("%d", &p);printf("%d\n", query(p));}}return 0;
}

查看全文

http://www.lryc.cn/news/45257.html