NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》
论文地址:https://arxiv.org/abs/2003.08934
推荐代码:https://github.com/yenchenlin/nerf-pytorch
文章目录
- 前言
- 隐式表达
- NeRF的训练
- 位置编码
- 体渲染(Volume Rendering)
前言
对于三维重建方向的研究人员来说,NeRF的重要性不言自明。NeRF作为ECCV2022的最佳论文提名之一,是值得精读的经典论文之一。不过,NeRF所涉及的图形学知识过多,对于纯CVer阅读起来较为吃力。本文旨在用朴素易懂的概念来解释NeRF的基本原理。如有不明白之处,欢迎留言交流~
NeRF,全称Neural Radiance Field,即神经辐射场。要了解NeRF,首先要知道NeRF是干嘛的,答:三维场景的新视角合成。NeRF是一种使用神经网络来隐式表达3D场景的技术。
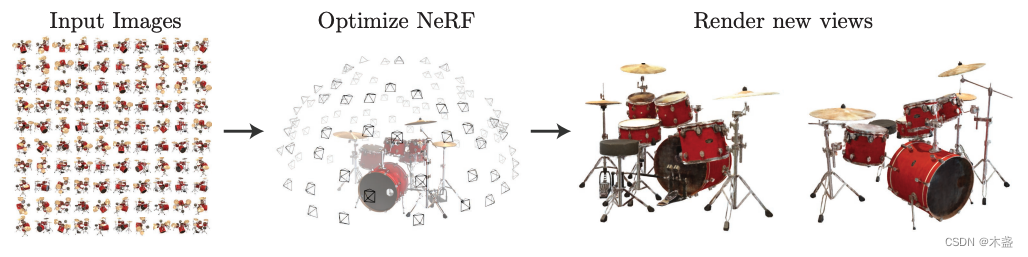
隐式表达
所谓隐式表达,与之相对的就是显式表达。假设我们用NeRF学习了一个确定场景,那么这个场景被隐式地保存在NeRF神经网络的参数中,加入我们需要得到一个新视角的画面,我们需要用神经网络计算出这个画面各个位置的光线和颜色值。
为了更方便理解,我用2D图像表示来举例:
我们有一张2D图像,像素点的坐标是(x,y)(x,y)(x,y),像素点的颜色是(r,g,b)(r,g,b)(r,g,b)。既然坐标和颜色是一一对应的,我们是否可以构建一种映射关系呢?
FΘ(x,y)=(r,g,b)(1)F_{\Theta}(x,y)=(r,g,b)\tag{1}FΘ(x,y)=(r,g,b)(1)
这种映射关系可以被神经网络来表达:
(x,y)→NN→(r,g,b)(2)(x,y)\rightarrow NN \rightarrow (r,g,b)\tag{2}(x,y)→NN→(r,g,b)(2)
我们可以对图像采样一些随机点当作神经网络的训练数据,然后可以用训练好的神经网络来推理这张图像其他位置像素值。这里很好理解,我们直接将这种情况推广到3D,就可以得到NeRF的基本结构。NeRF的公式表达:
FΘ:(x,d)→(c,σ)(3)F_{\Theta}:(\bold{x},\bold{d}) \rightarrow(\bold{c},\sigma)\tag{3}FΘ:(x,d)→(c,σ)(3)
式(3)中的x=(x,y,z)\bold{x}=(x,y,z)x=(x,y,z)表示3D点的坐标,d=(θ,ϕ)\bold{d}=(\theta,\phi)d=(θ,ϕ)表示观测方向,c=(r,g,b)\bold{c}=(r,g,b)c=(r,g,b)表示3D点预测出来的颜色值,σ\sigmaσ表示体密度(一会儿着重解释)。我们对比式(1)和式(3)可以发现一些区别,由平面推广到3D要考虑很多东西,首先一点就是观测角度会影响3D点的颜色表现。所以,整个NeRF的设计就是一套view-dependent的思路,所以NeRF的输入除了3D位置以外,还需要观测角度,一共需要5D向量作为输入,即(x,y,z,θ,ϕ)(x,y,z,\theta,\phi)(x,y,z,θ,ϕ)。输出结果为该3D点的像素值c\bold{c}c和体密度σ\sigmaσ,这两个输出可以用来进行体渲染(volume rendering)。
NeRF的训练
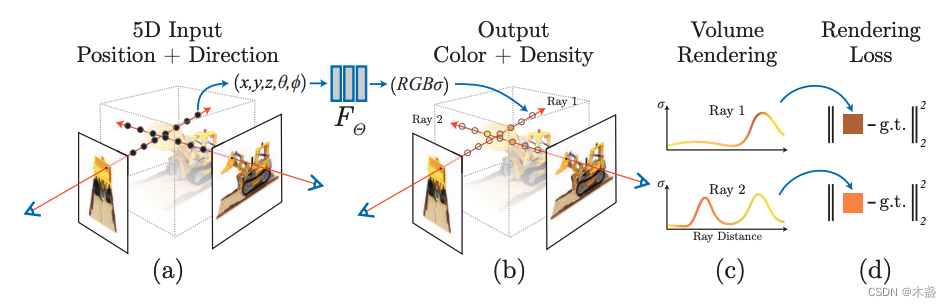
从图2我们可知,NeRF是5D输入(x,y,z,θ,ϕ)(x,y,z,\theta,\phi)(x,y,z,θ,ϕ)和4D输出(r,g,b,σ)(r,g,b,\sigma)(r,g,b,σ)。如子图(a)所示,对于某已知视图,我们可以对每个2D点作出射线,然后沿着射线的方向(即深度方向)做多个点的采样,至于射线原理不太明白请了解一下相机二维坐标和三维坐标的映射关系(《【AI数学】相机成像之内参数》)。
位置编码
γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))(4)\gamma(p)=\left(\sin \left(2^0 \pi p\right), \cos \left(2^0 \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)\tag{4}γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))(4)
体渲染(Volume Rendering)
C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt,where T(t)=exp(−∫tntσ(r(s))ds)(5)C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right) \tag{5}C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt, where T(t)=exp(−∫tntσ(r(s))ds)(5)
∑i=1NTiαici(6)\sum_{i=1}^N T_i \alpha_i c_i\tag{6}i=1∑NTiαici(6)
Ti=∏j=1i−1(1−αj)(8)T_i=\prod_{j=1}^{i-1}\left(1-\alpha_j\right)\tag{8}Ti=j=1∏i−1(1−αj)(8)
αi=1−e−σiδti(9)\alpha_i=1-e^{-\sigma_i \delta t_i}\tag{9}αi=1−e−σiδti(9)
