【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|
- <二叉树的遍历>
- 1.前序遍历【递归】
- 2.中序遍历【递归】
- 3.后序遍历【递归】
- 4.层序遍历【非递归】
- 4.1判断是否是完全二叉树
<二叉树的遍历>
在学习二叉树遍历之前我们先了解下二叉树的概念。
二叉树是:
1.空树
2.非空:根节点,根节点的左子树,根节点的右子树构造。
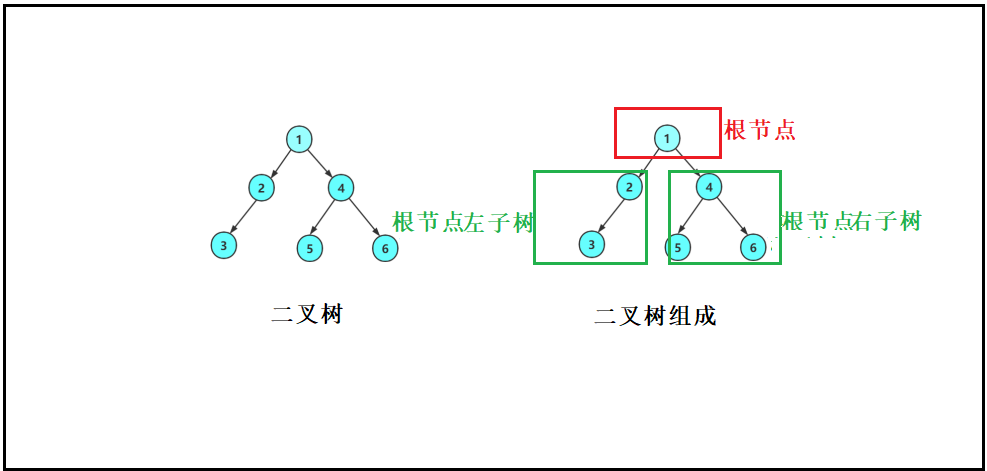
学习二叉树结构,最简单的方式就是遍历了。
二叉树的遍历就是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个节点只操作一次。
访问结点所做的操作依赖于具体的应用问题。
二叉树的遍历分为
1.<前序遍历>[Preorder Traversal]
访问根节点的操作发生在遍历左右子树之前。
也就是对于一个节点,它要求先访问这个节点的内容,然后再去遍历左子树,当左子树遍历完后,再遍历右子树。
2.<中序遍历>[Inorder Traversal]
访问根节点的操作发生在遍历其左右子树之中
也就是对于一个节点,它要求先遍历左子树,当左子树都遍历完,再回来访问节点里的内容,然后再遍历右子树。
3.<后续遍历>[Postorder Traversal]
访问根节点的操作发生在遍历其左右子树之后
也就是对于一个节点,它要求先遍历完左子树,再遍历完右子树,最后回来的时候再访问节点的内容。
4.<层序遍历>
层序遍历,顾名思义,一层一层的遍历即可。
从第一层开始遍历,遍历完第一层再遍历下一层。
我们为了好验证二叉树的遍历操作,手动创造一个二叉树,也就是下图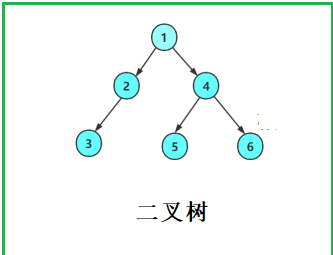
这样,用代码来实现就是这样:
#include <stdio.h>
#include <stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{BTNode* ret =(BTNode*)malloc(sizeof(BTNode));ret->data = x;ret->left = NULL;ret->right = NULL;return ret;
}
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
1.前序遍历【递归】
我们为了真正展现前序遍历在二叉树中是如何实现的,将空节点也打印出来。这样就可以清晰的看出来遍历的过程。
// 二叉树前序遍历-<根节点-左子树-右子树>-
void PreOrder(BTNode* root)
{if (root == NULL)//如果遇到空节点就返回{printf("NULL ");return;}printf("%d ", root->data);//先访问根节点内容,打印完节点内容后再进入左子树。PreOrder(root->left);//进入左子树PreOrder(root->right);//进入右子树
}
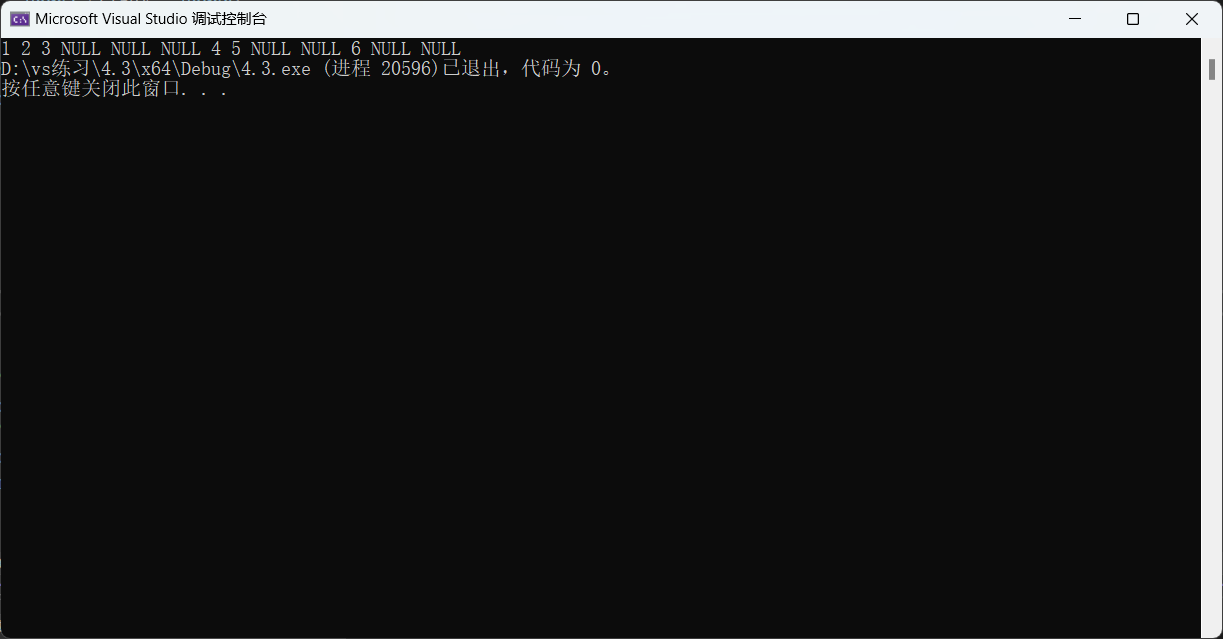
根据结果你能想明白怎么遍历的吗?
递归展开图:
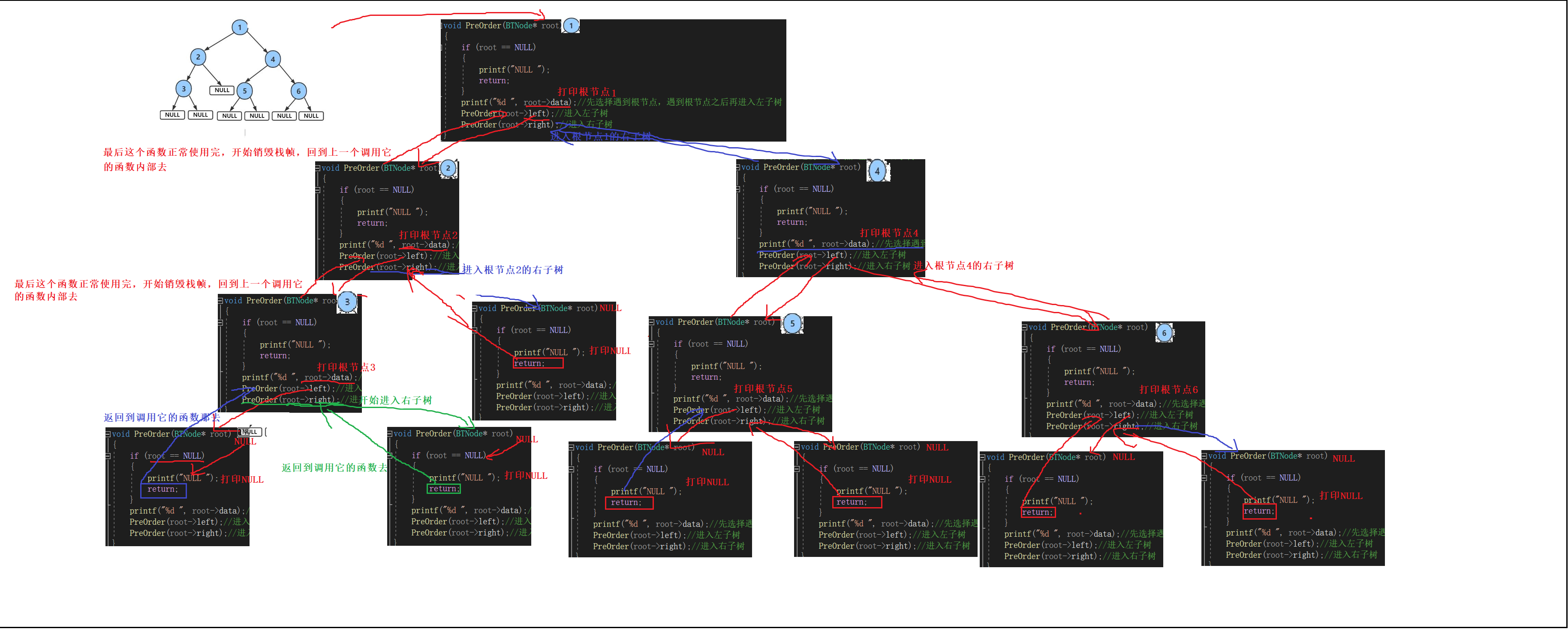
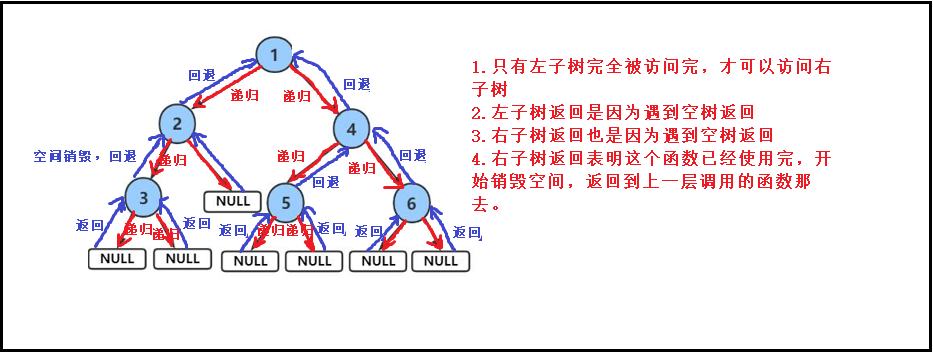
2.中序遍历【递归】
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);//先遍历左子树printf("%d ", root->data);//遍历完左子树后再访问节点内容InOrder(root->right);//访问完节点内容后再遍历右子树
}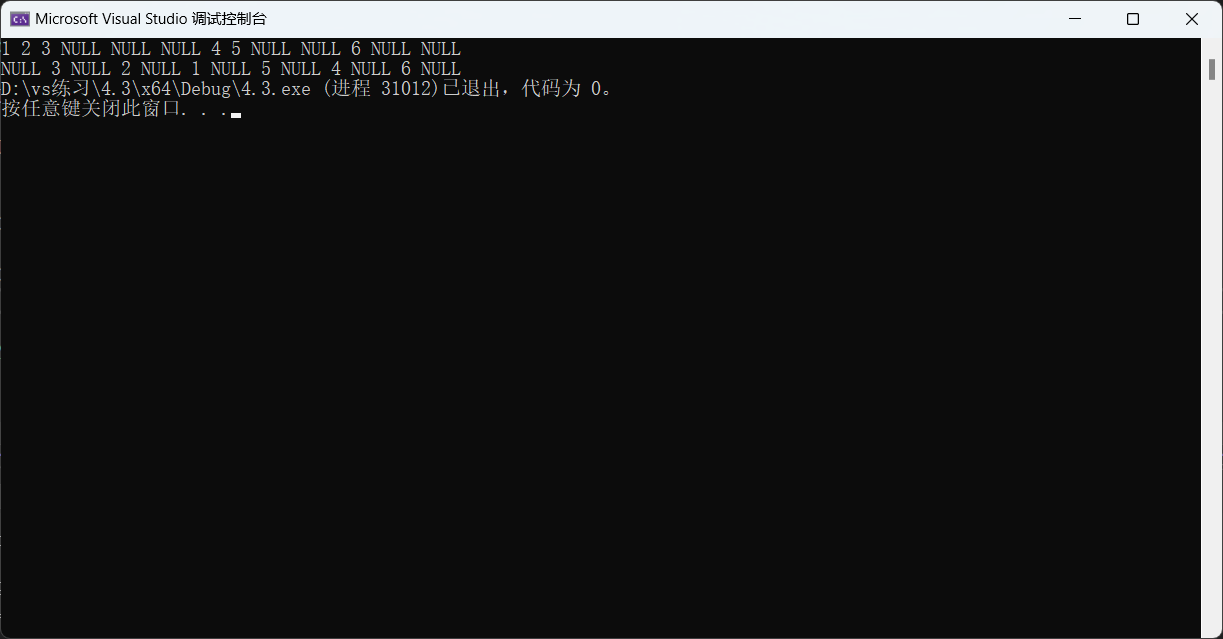
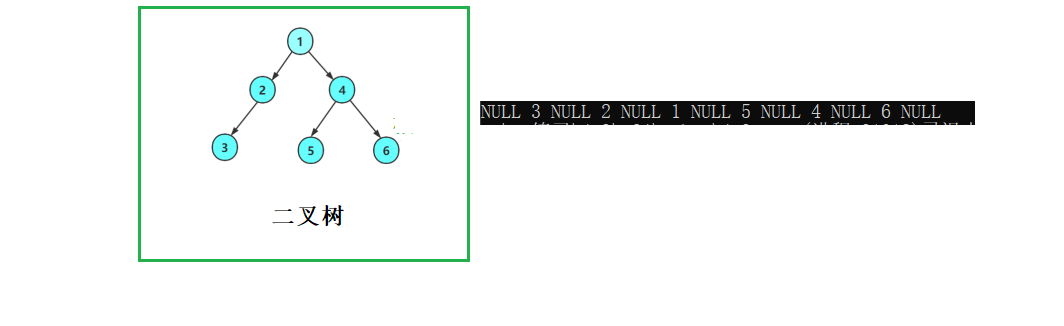
递归展开图
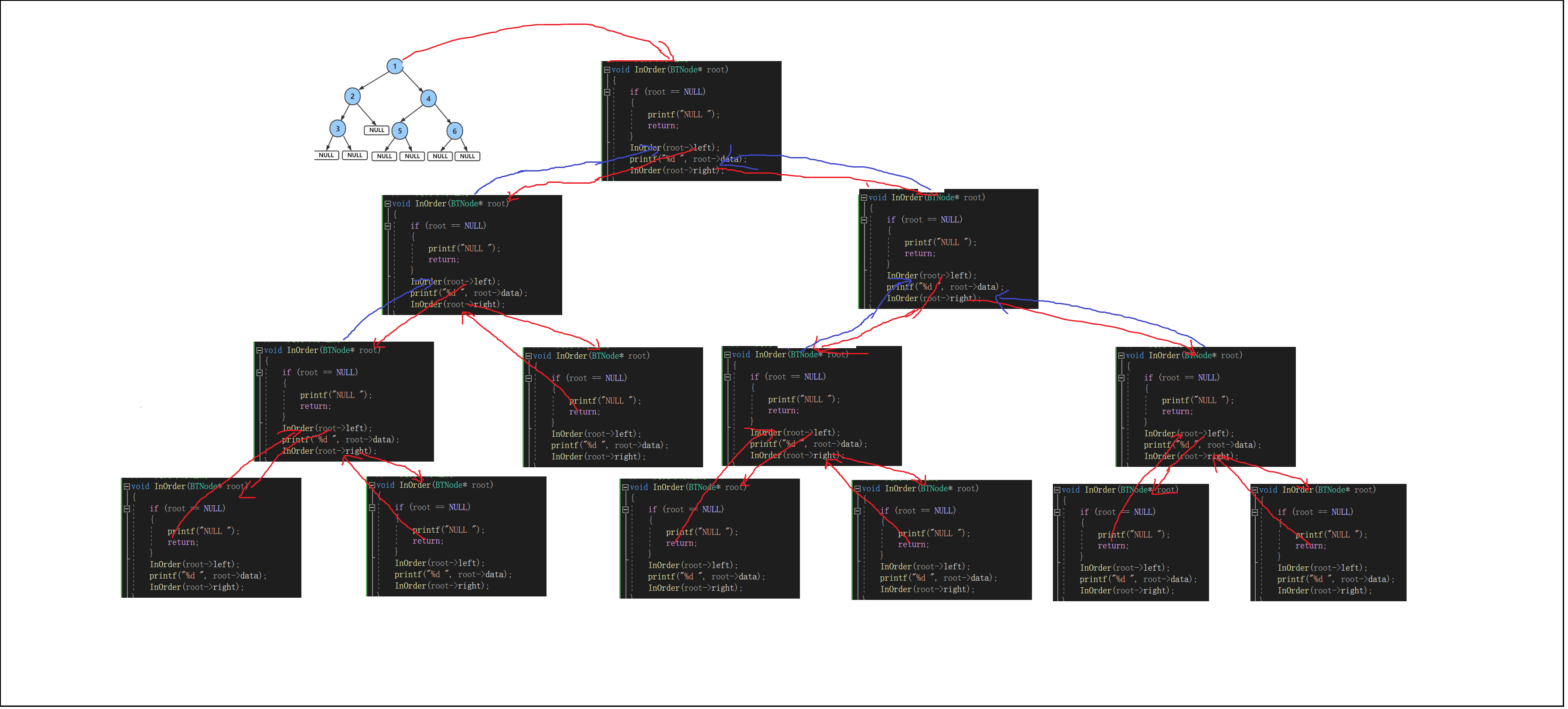
3.后序遍历【递归】
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

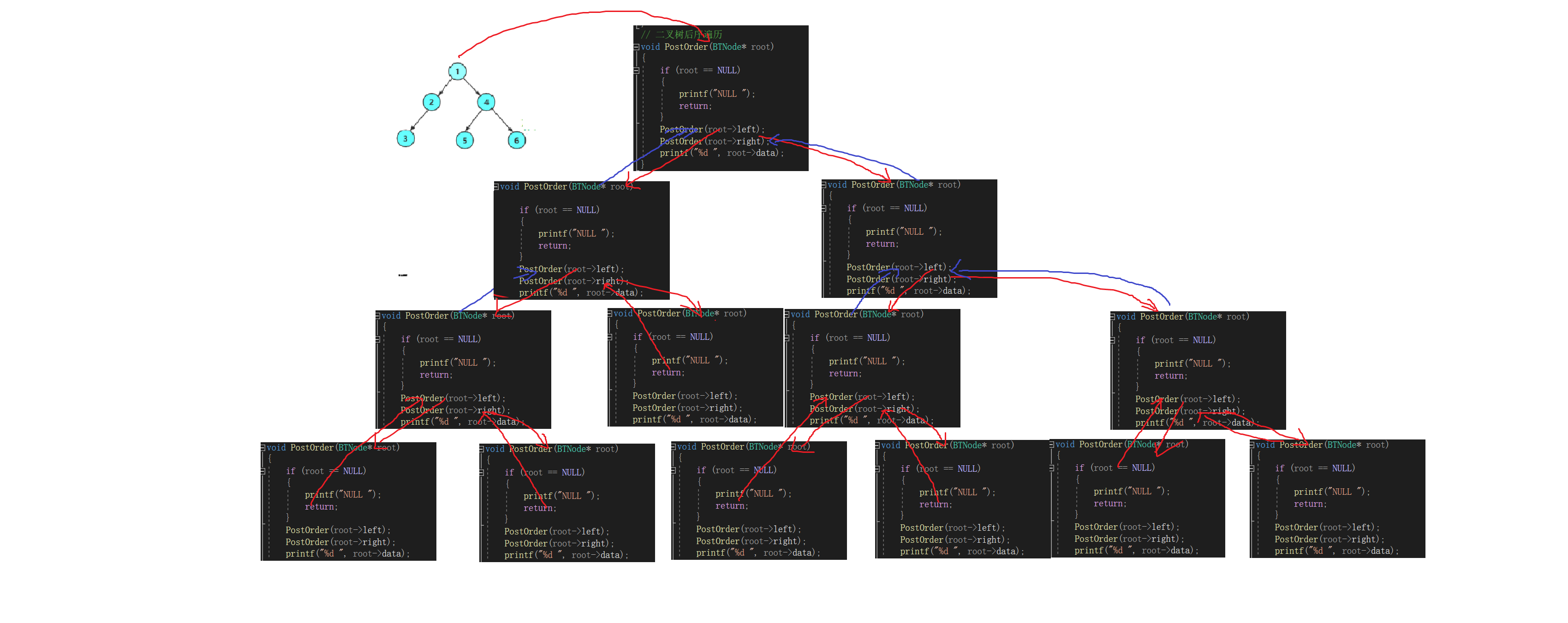
而后序遍历这种特点很适合用在二叉树的销毁上去。
因为相比较前序遍历,如果先销毁了节点,那它的左右子树就无法找到了。
但后续遍历不一样,后序遍历是先遍历左右子树,最后再访问节点。
所以我们只要使用后序遍历,先销毁左右子树,再销毁节点就可以了。
比如:二叉树的销毁
void BTreeDestroy(BTNode* root)
{if (root == NULL){return;}BTreeDestroy(root->left);//先销毁左子树BTreeDestroy(root->right);//再销毁右子树free(root);//最后再销毁节点root = NULL;
}
4.层序遍历【非递归】
上面三个都是属于递归形式的遍历,层序遍历是非递归的。
怎么进行层序遍历呢?
这个就需要用到队列来解决了。
思想:
出上一层,带入下一层。
一开始让根节点入队列,那队列中就有元素存在,不是空队列了。
然后接下来就是不断的出队列中的根节点,每一次出队列中的根节点时,都要将
该根节点的孩子插入到队列的后面去。 也就是出根节点,带入它们的孩子进来。直到队列中没有数据为止。
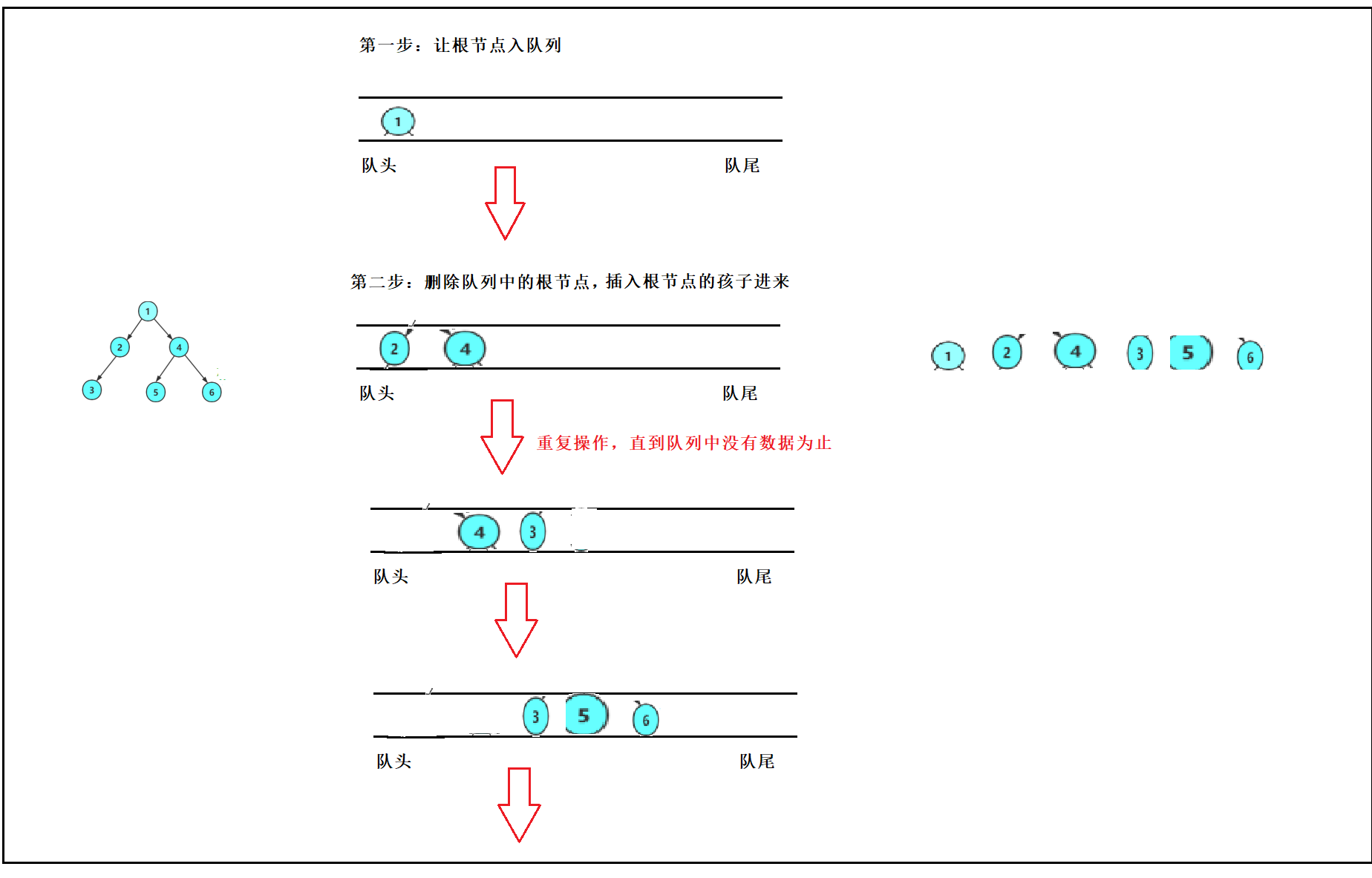
不过注意的是,队列中不是真正节点,而是指向节点的指针,如果将节点插入进去,那怎么找到它们的孩子呢?
所以我们插入进入的是指向节点的指针。
typedef struct BTreeNode* QData;//注意这里将队列中元素的类型改成指向节点的指针
typedef struct QNode
{struct QNode* next;QData data;//队列的元素是指向节点的指针
}QNode;
//因为队列的数据结构操作需要找尾,这就需要传多个参数了,很麻烦,所以我们再分装个结构体将多个数据变成一个
typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QueueInit(Queue *pq);//初始化队列
void QueueDestroy(Queue *pq);//销毁队列
void QueuePush(Queue*pq ,QData x);//入队,从队尾插入一个数据,尾删
void QueuePop(Queue *pq);//出队,从队头删除数据,头删
bool QueueEmpty(Queue *pq);//判断队列是否为空
int QueueSize(Queue*pq);//获得队列有效数据个数大小
QData QueueFront(Queue*pq);//获取队头数据
QData QueueBack(Queue*pq);//获取队尾数据
#include "queue.h"
void QueueInit(Queue* pq)//初始化队列
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}
void QueueDestroy(Queue* pq)//销毁队列
{QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}
void QueuePush(Queue* pq, QData x)//入队,从队尾插入一个数据,尾删
{assert(pq);
/* QNode* cur = pq->head;*/QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");}newnode->data=x;newnode->next = NULL;if (pq->head == NULL){//赋值pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;//更新tail的位置pq->tail = newnode;}pq->size++;}
void QueuePop(Queue* pq)//出队,从队头删除数据,头删
{assert(pq);//头删之前需要判断链队列是否为空assert(pq->head!=NULL);QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head==NULL)//只管头删,最后再处理。{pq->tail=NULL;}pq->size--;
}bool QueueEmpty(Queue* pq)//判断队列是否为空----主要size的作用
{assert(pq);return pq->size == 0;//return pq->head=pq->tailk=NULL;
}
int QueueSize(Queue* pq)//获得队列有效数据个数大小
{assert(pq);return pq->size;
}QData QueueFront(Queue* pq)//获取队头数据
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QData QueueBack(Queue* pq)//获取队尾数据
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}以上是创建一个队列,接下来就是进行二叉树的层序遍历了。
void LevOlder(BTNode* root)//层序遍历--
{Queue q;//定义一个队列QueueInit(&q);//初始化队列//首先将根 指针插入到队列里去if (root){QueuePush(&q, root);}//再出上一层带入下一层while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//保存一下这个要出队列的指向结点的指针QueuePop(&q);printf("%d ", front->data);//出完后再将它的孩子指针带入进来if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
4.1判断是否是完全二叉树
如何判断一个二叉树树是否是完全二叉树呢?
首先我们需要了解什么是完全二叉树
【完全二叉树】
1.前n-1层都是满的二叉树。
2.最后一层从左到右是连续的。
特点:
1.非空节点是连续的。
2.空节点也是连续的。
3.至多有一个度为1的节点。
我们根据完全二叉树非空节点都是连续的这一特性,来作下面的思路:
如果对完全二叉树进行层序遍历,那么第一次出现空节点的地方就是最后一个节点的后面。 而后面就不能再出现非空节点了,后面应该都是空。
所以我们可以做出这样判断:层序遍历二叉树,如果第一次出现空之后,再出现非空节点的一定不是完全二叉树,如果后面只有空则是完全二叉树。
不过要注意的是,这里的层序遍历与原来的层序遍历不一样,原来的层序遍历,只会将根节点插入到队列中去,不会将空节点插入到队中去,而现在需要将空节点也插入到队列中去,如果出队列中的元素,出出队列的是一个空节点,那么我们就可以进行判断,是否后面还会出现非空节点呢?
//判断是否是完全二叉树,利用完全二叉树性质--非空结点是连续的,一旦出现空,后面就不应该再出现空结点。所以利用层序遍历,当第一次出现
//空时,就可以进行判断后面是否会出现非空结点。这里不同与普通层序遍历,NULL也进队列,而且出队列的结点有两种可能一种为空,一种不为空,不像层序遍历只出非空结点
{
bool BTreeCompele(BTNode* root)
{Queue q;QueueInit(&q);if (root)//将根节点插入到队列中{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//出队列中的元素if (front == NULL){break;}//如果front不为空,就将它的孩子插入到队列中去,空节点也插入进去,不需要讨论QueuePush(&q, front->left);QueuePush(&q, front->right);}//break 跳出来需要判断是否后面还会出现非空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//出队列中的元素if (front)//如果队列中出的节点不为空节点{QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

