分治法实现合并排序(归并排序),理解分治算法思想,实现分治算法的完美例子合并排序(含码源与解析)

🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏
🪔本系列专栏 - 数据结构与算法_勾栏听曲_0
🍻欢迎大家 🏹 点赞👍 评论📨 收藏⭐️
📌个人主页 - 勾栏听曲_0的博客📝
🔑希望本文能对你有所帮助,如有不足请指正,共同进步吧🏆
🎇一个人无论在祈祷什么,他祈祷的都只不过是一个奇迹。所有祈祷文无非都是一个意思:“伟大的上帝啊,请使二乘二不等于四吧!”📈
分治法
算法思想
时间效率分析
合并排序
分治法
算法思想
分治法可能是最著名的通用算法设计技术了。虽然它的名气可能和它那好记的名字有关,但它的确是当之无愧的:很多非常有效的算法实际上就是这个通用算法的特殊实现。其实,分治法是按照以下方案工作的。
(1)将一个问题划分为同一类型的若干子问题,子问题最好规模相同。
(2)对这些子问题求解(一般使用递归方法,但在问题规模足够小时,有时也会利用另一个算法)。
(3)有必要的话,合并这些子问题的解,以得到原始问题的答案。
分治法的流程可以参见下图,该图描述的是将一个问题划分为两个较小子问题的例子,也是最常见的情况(至少那些设计运行在单CPU机器上的分治算法是这样的)。

时间效率分析
在分治法最典型的运用中,问题规模为n的实例被划分为两个规模为n/2的实例。更一般的情况下,一个规模为n的实例可以划分为b个规模为n/b的实例,其中α个实例需要求解(这里,a和b是常量,a≥1,b>1)。为了简化分析,我们假设n是b的幂,对于算法的运行时间T(n),我们有下列递推式:
T(n) =aT(n / b)+ f(n)
其中,f(n)是一个函数,表示将问题分解为小问题和将结果合并起来所消耗的时间(对于求和的例子来说,a = b = 2,f(n)= 1)。上述递推式被称为通用分治递推式(generaldivide-and-conquer recurrence)。显然,T(n)的增长次数取决于常量a和b的值以及函数f(n)的增长次数。在分析许多分治算法的效率时,可以应用下列定理来大大简化我们的工作。
主定理 如果在递推式(5.1)中 f(n)e e(n*),其中d≥0,那么
其中,当a < 时,该问题的时间复杂度为n的d次方
当a = 时,该问题的时间复杂度为n的d次方乘一个对数级
当a > 时,该问题的时间复杂度为n的log b为底a次方
合并排序
合并排序是成功应用分治技术的一个完美例子。对于一个需要排序的数组A[0..n -1],合并排序把它一分为二:A[0..[n / 2| - 1]和A[ [n / 2 ]..n-1],并对每个子数组递归排序,然后把这两个排好序的子数组合并为一个有序数组。
下图演示的是用合并排序算法对数列8,3,2,9,7,1,5,4进行排序的操作过程。
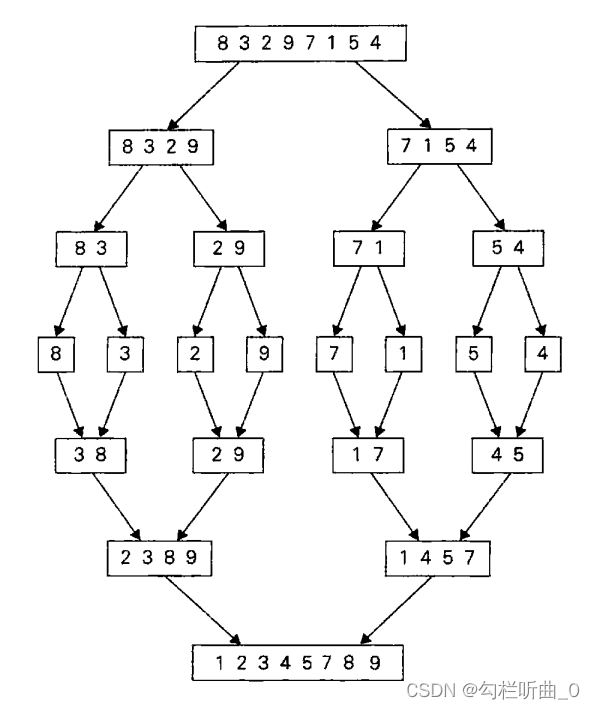
接下来通过视频演示来了解合并排序算法对数列8,3,2,9,7,1,5,4进行排序的操作过程。
合并排序_分治法
代码实现:
#include <stdio.h>void merge(int arr[], int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;/* 创建临时数组 */int L[n1], R[n2];/* 复制数据到临时数组 arrays L[] 和 R[] */for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1+ j];/* 归并临时数组到 arr[l..r]*/i = 0; // 初始化第一个子数组的索引j = 0; // 初始化第二个子数组的索引k = l; // 初始归并子数组的索引while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;}else {arr[k] = R[j];j++;}k++;}/* 复制 L[] 的保留元素 */while (i < n1) {arr[k] = L[i];i++;k++;}/* 复制 R[] 的保留元素 */while (j < n2) {arr[k] = R[j];j++;k++;}
}/* l 为左侧索引,r 为右侧索引 */
void mergeSort(int arr[], int l, int r) {if (l < r) {// 求中间位置,防止 (l+r) 的和超过 int 类型最大值int m = l+(r-l)/2;// 递归排序左半部分mergeSort(arr, l, m);// 递归排序右半部分mergeSort(arr, m+1, r);// 合并merge(arr, l, m, r);}
}
