Mysql深度分页优化的一个实践
问题简述:
最近在工作中遇到了大数据量的查询场景, 日产100w左右明细, 会查询近90天内的数据, 总数据量约1亿, 业务要求支持分页查询与导出.
无论是分页或导出都涉及到深度分页查询, mysql通过limit/offset实现的深度分页查询会存在全表扫描的问题, 比如offset=1000w, limit=10, 那么mysql会依次加载1000w条数据进行查找, 然后扔掉前1000w条, 然后返回找到的第1000w后的10条, 这种显然是傻瓜式的实现,显然会对内存和IO带来大量的消耗, 可想而知其耗时肯定会随着数据量的加大而上涨, 给个示例: 来源于[1]
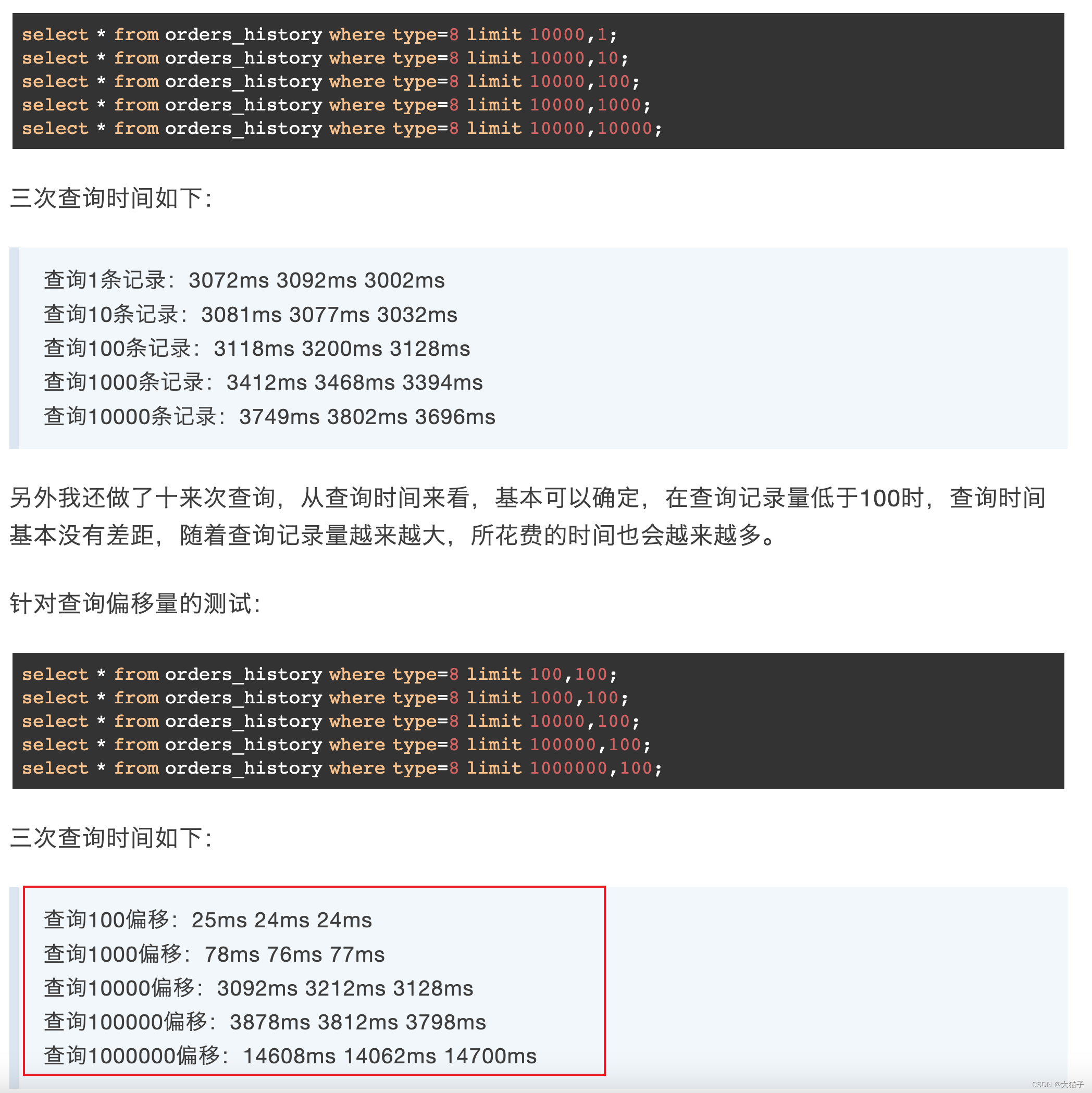
问题原因是mysql针对这种深度分页的近似全表扫描的操作导致: 参考[2]:
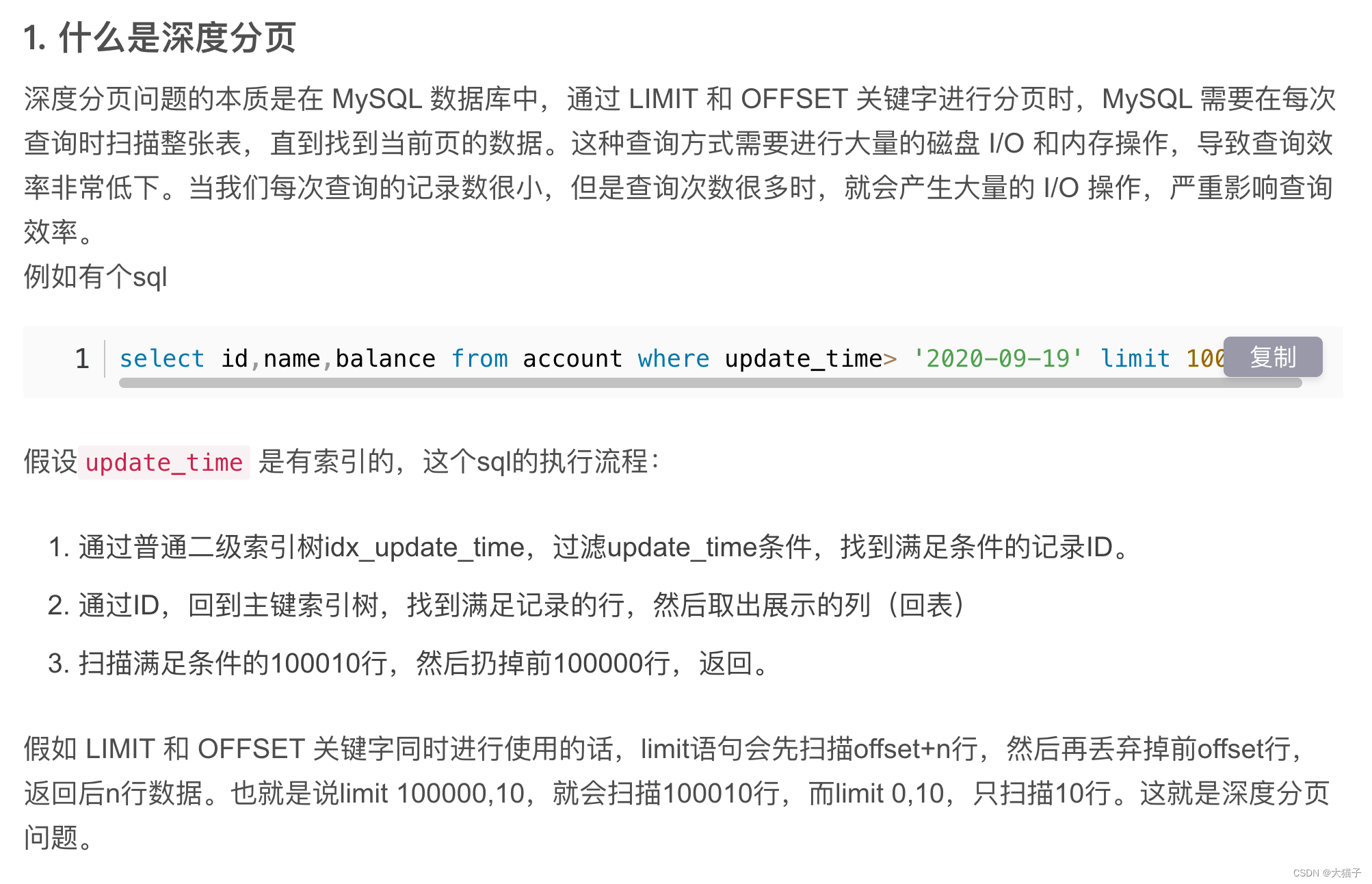
那么如何优化呢? 确保深度分页时耗时稳定, 与页码无关, 与数据量规模无关:
- 前端加一些限制: 限定不能任意跳转, 只能进行上一页与下一页的翻页操作, 业务能接受这种逻辑
- 后端针对翻页查询操作, 会记录上一次的id最大值与最小值, 在查询时通过标签过滤的方式过滤掉已翻页的数据, offset始终值为0
- 针对导出逻辑, 则很简单, 都无需考虑上一页, 一直下一页翻页处理即可.
这种处理也叫做标签记录法, 就是利用索引过滤来规避掉全表扫描问题的一种优化方式, 另外一种是子查询, 类似的操作, 只是即无需记录上次查询的结果, 每次查询时都重新查询下指定偏移量的最后一条记录, 将其ID作为过滤项或边界值, 然后进行查询, 本质是标签记录法, 换汤不换药
借用下[2]中的子查询的例子:
select id,name,balance FROM account where id >= (select a.id from account a where a.update_time >= '2020-09-19' limit 100000, 1) LIMIT 10;我觉得还是标签记录法性能时最好的, 一次查询解决. 就是要想办法维护下边界值, 尽量避免随机跳转.
另外近似深度分页的概念: 内存分页, 内存分页也是一种全表扫描的操作, 但是在应用层的过滤处理逻辑, 先获取全部数据, 然后在应用程序中对数据做处理, 数据量较小且sql逻辑复杂时会采取这种方式, sql中不建议加入太多代码逻辑, 调试与维护困难不说, 容易造成慢sql查询.
参考:
[1]:MySQL分页查询优化
[2]: MySQL深度分页-CSDN博客
