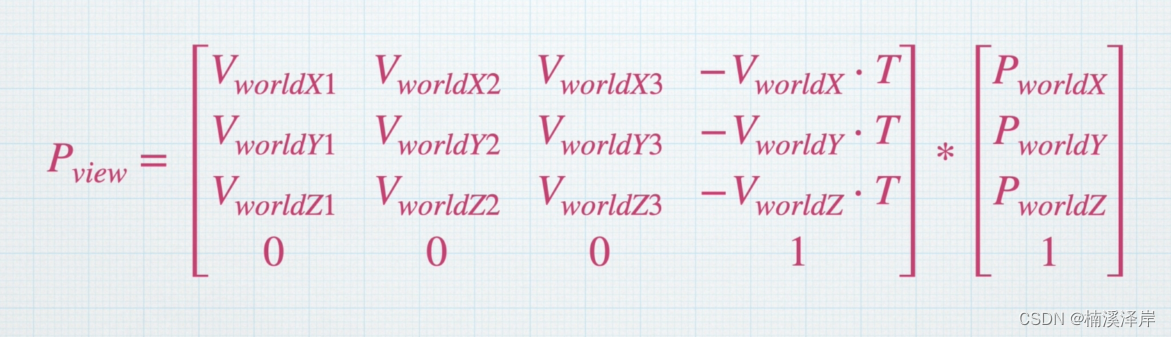Unity中Shader观察空间推导
文章目录
- 前言
- 一、本地空间怎么转化到观察空间
- 二、怎么得到观察空间的基向量
- 1、Z轴向量
- 2、假设 观察空间的 Y~假设~ = (0,1,0)
- 3、X = Y 与 Z 的叉积
- 4、Y = X 与 Z 的叉积
- 三、求 [V~world~]^T^
- 1、求V~world~
- 2、求[V~world~]^T^
- 四、求出最后在Unity中使用的公式
- 1、偏移坐标轴
- 2、把 平移的坐标 构建成之前文章中使用的 平移矩阵
- 3、化简我们的矩阵
前言
在上一篇文章中,我们推演了矩阵几何计算。
- Unity中Shader矩阵变换的几何体现
在这篇文章中,我们来推导一下 观察空间(摄像机空间)。
一、本地空间怎么转化到观察空间
可以根据上篇文章的推导得出:
- 在两个不同角度坐标系下的坐标信息转化可以由如下公式算出。
Pview = [Wview] * Pworld
[Wview] = [Vworld]-1 = [Vworld]T
Pview = [Vworld]T * Pworld
- Pview顶点在观察空间下的坐标
- Pworld顶点在世界空间下的坐标
- Wview世界空间的基向量 在 观察空间下的矩阵
- Vworld观察空间的基向量 在 世界空间下的矩阵
二、怎么得到观察空间的基向量
- 我们的观察空间使用的是右手坐标系
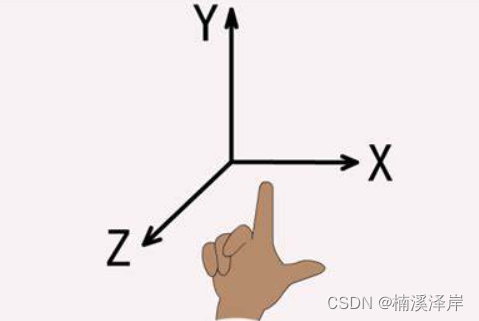
1、Z轴向量
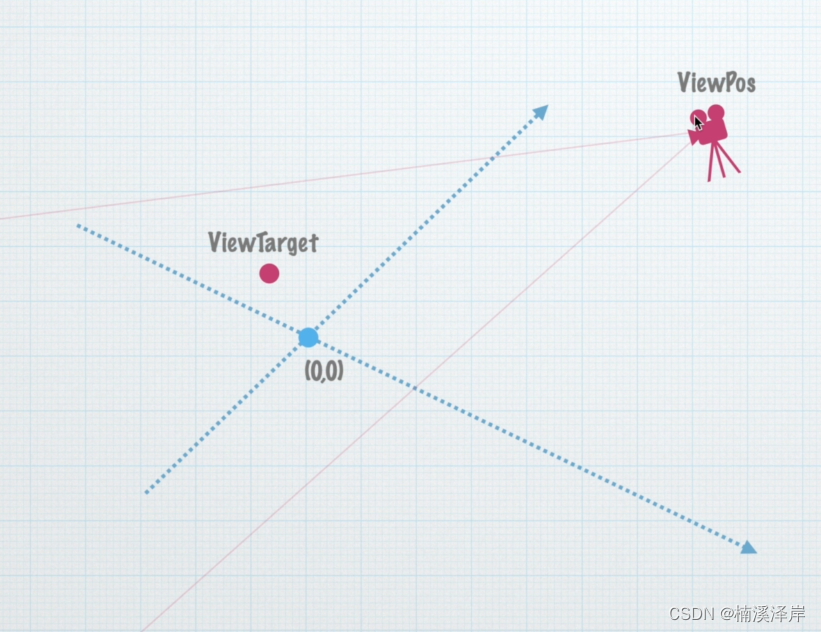
- Z轴正方向是从 模型顶点 指向 摄像机 方向
- Z = ViewPos - ViewTarget
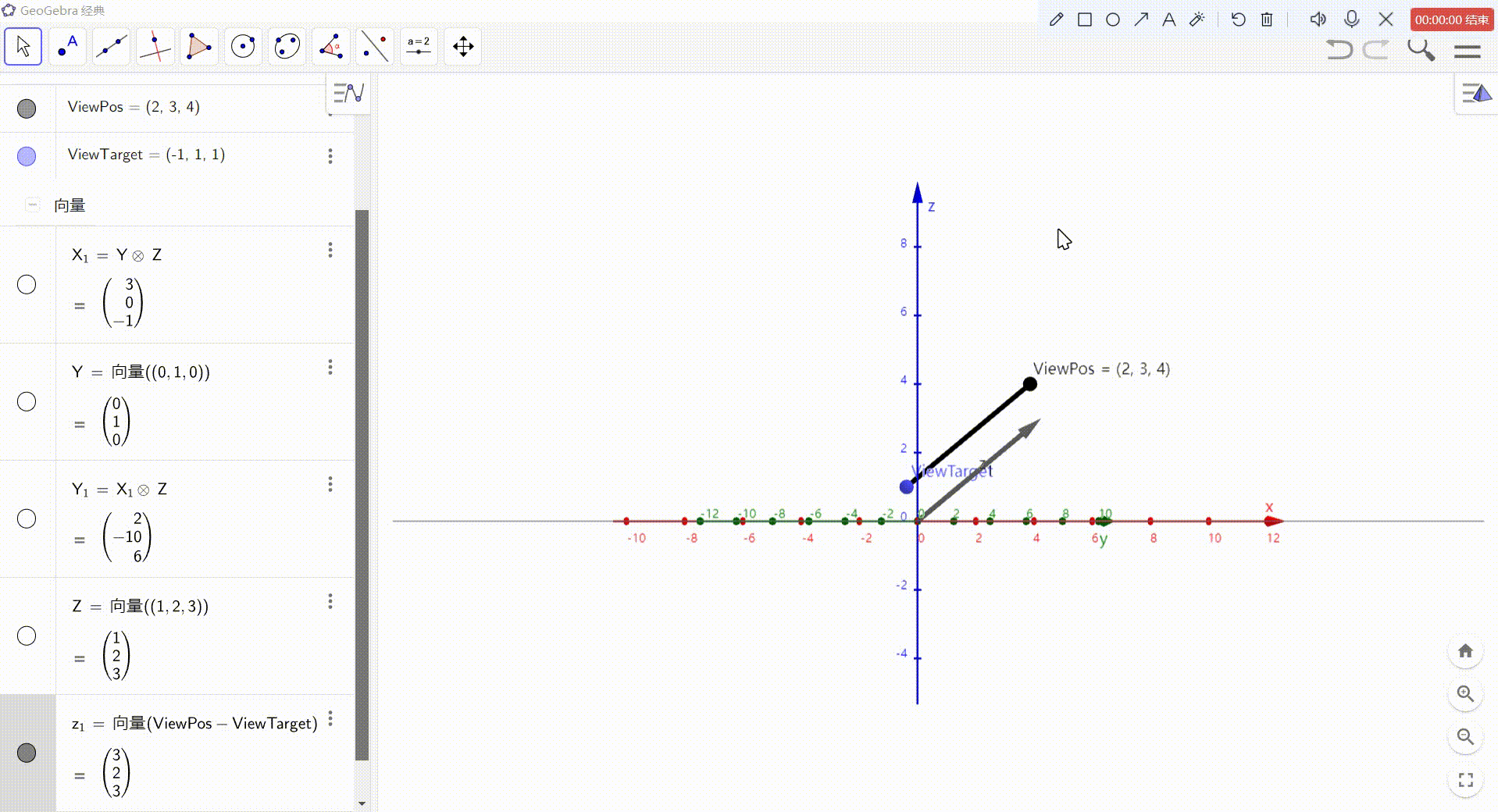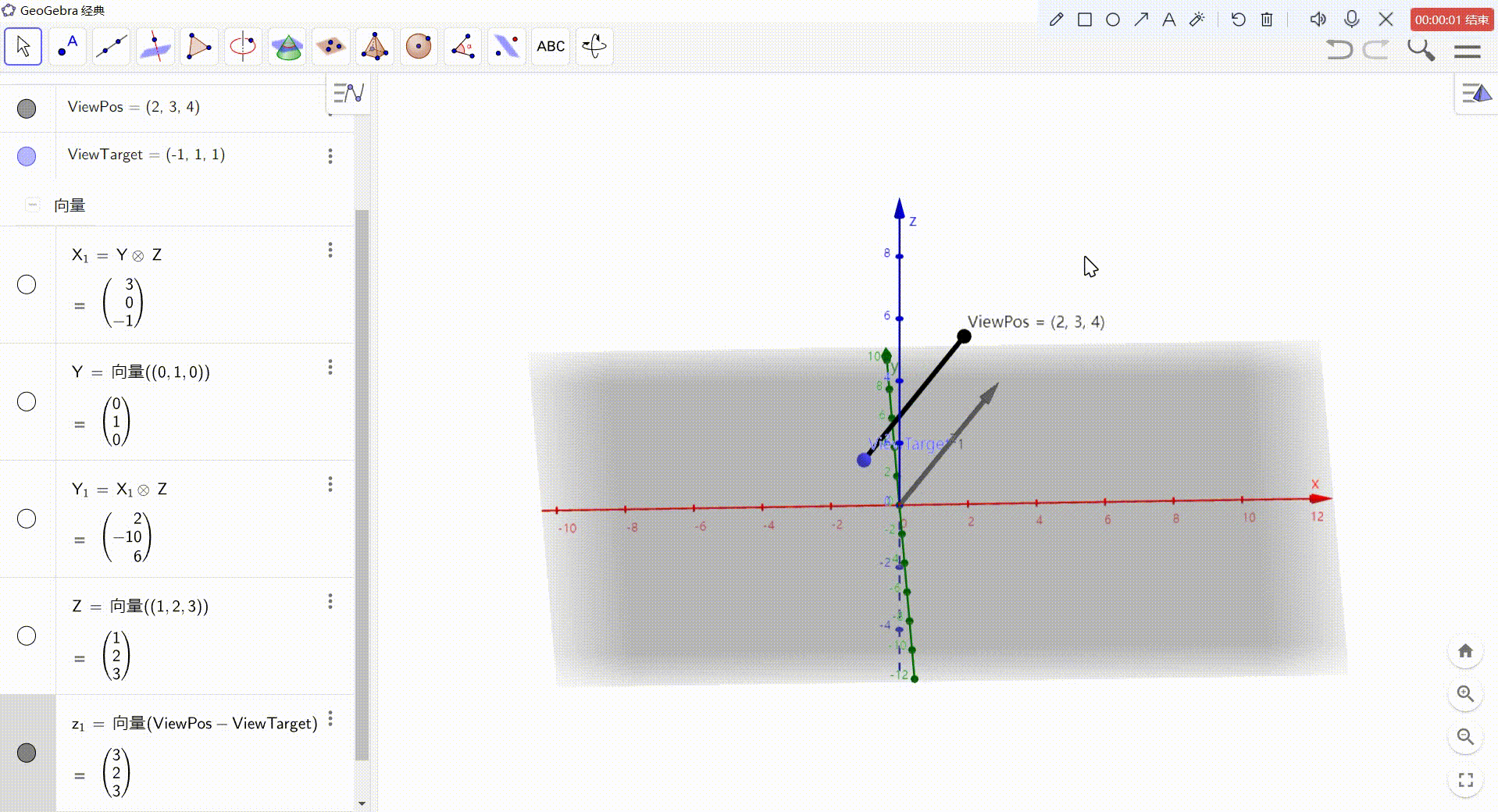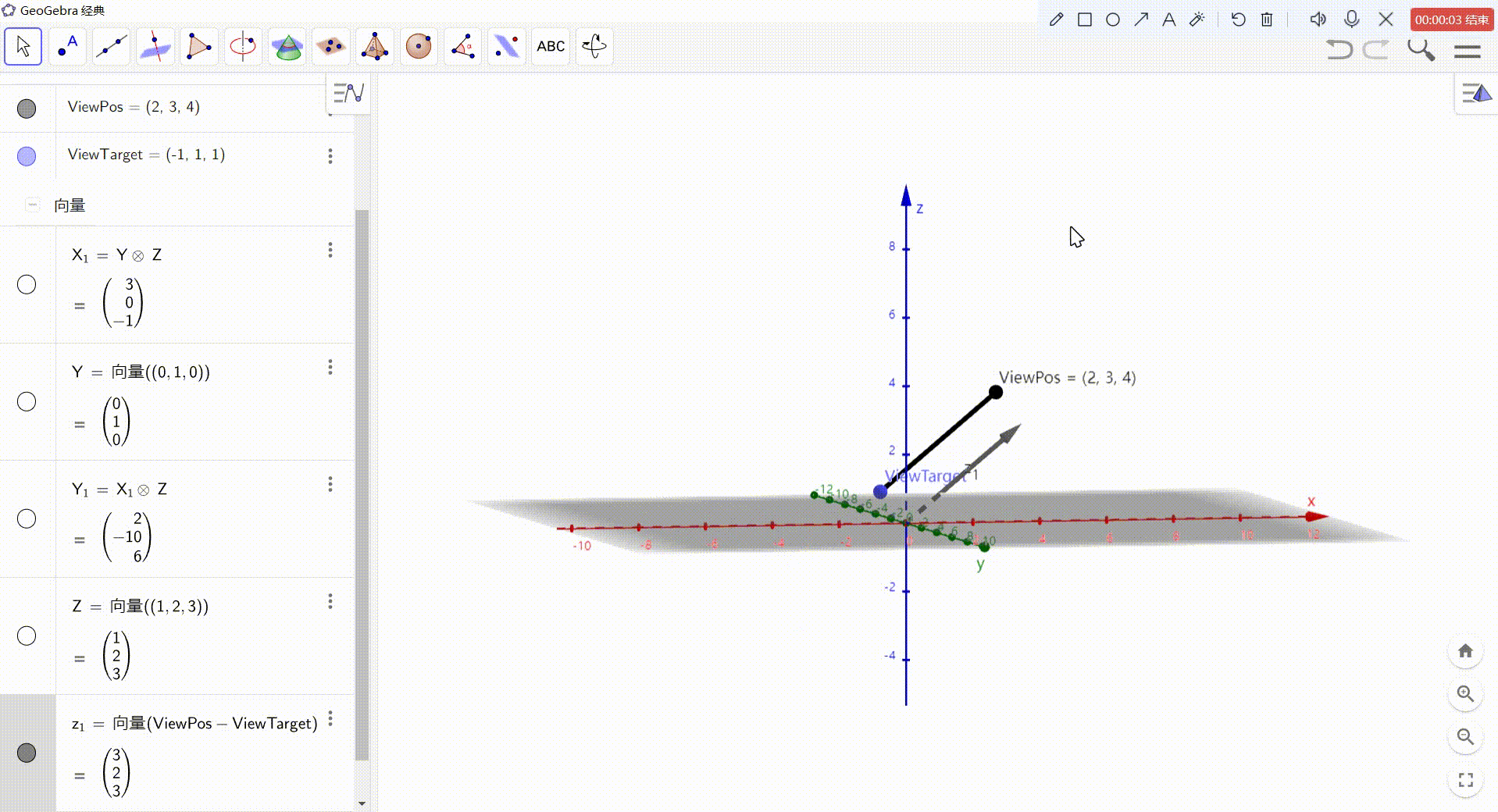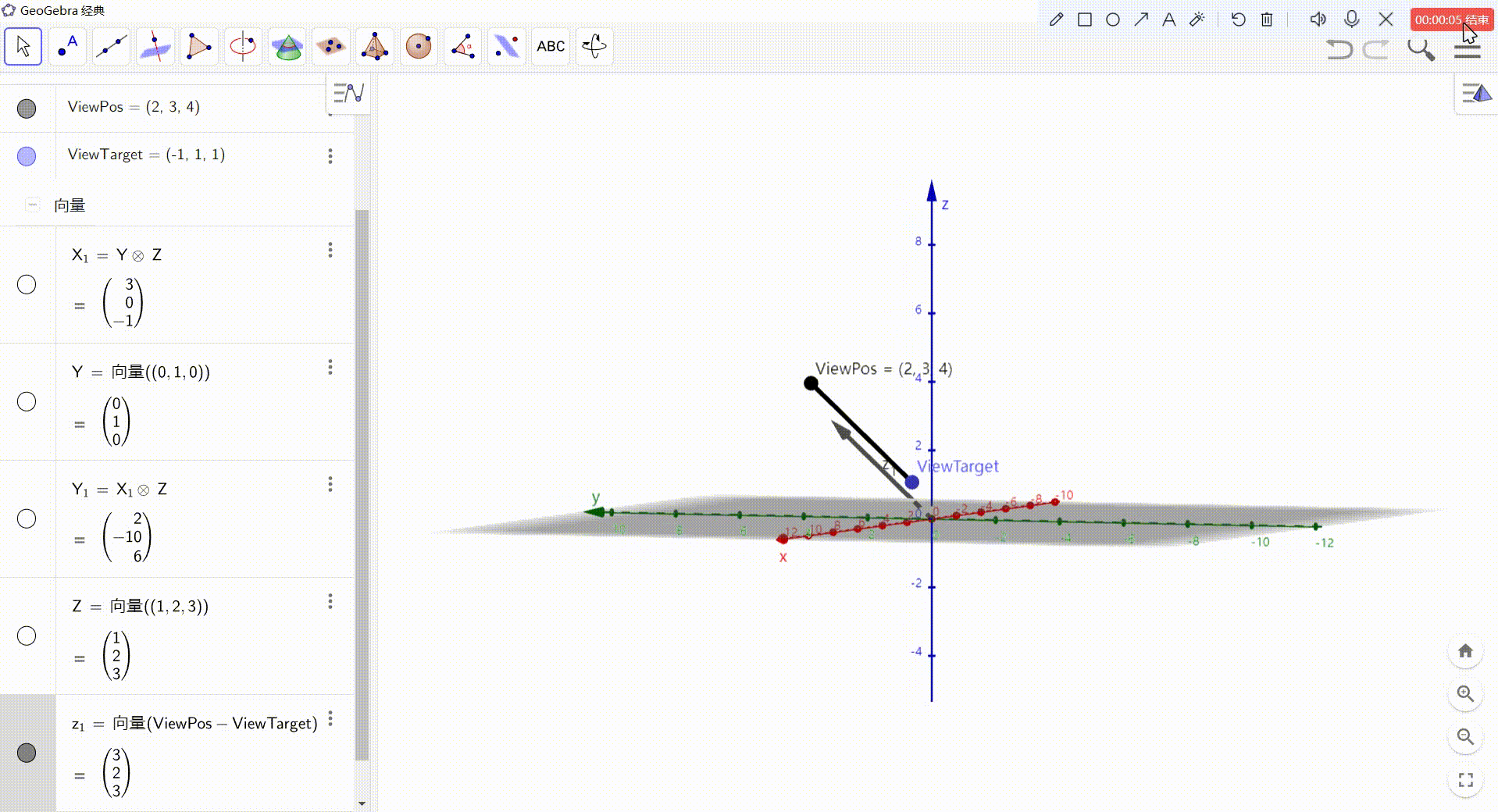
现在只知道 Z轴,还需要求 X Y轴。
2、假设 观察空间的 Y假设 = (0,1,0)
- X = Y 与 Z 的叉积
- Y = X 与 Z 的叉积
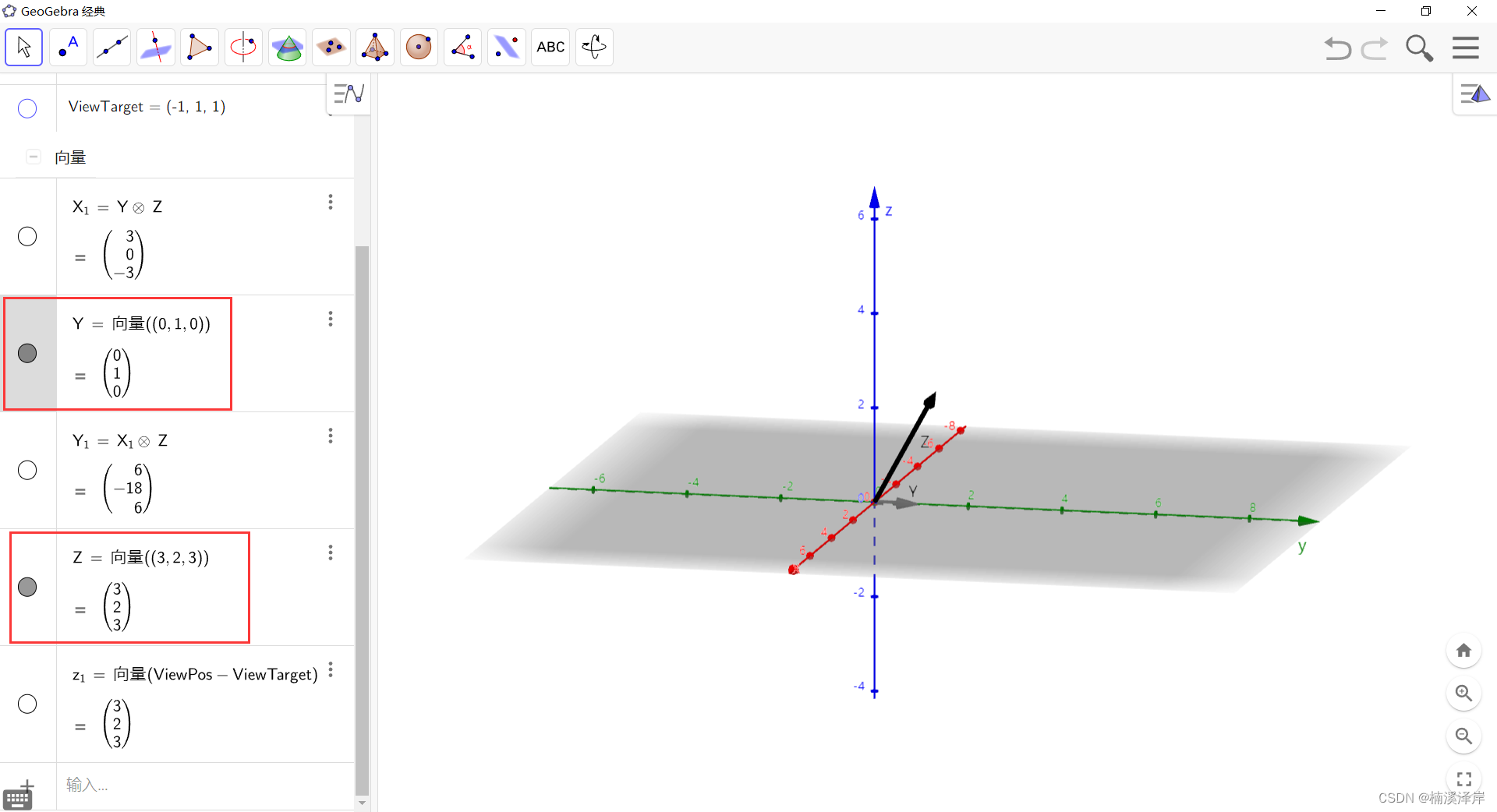
3、X = Y 与 Z 的叉积
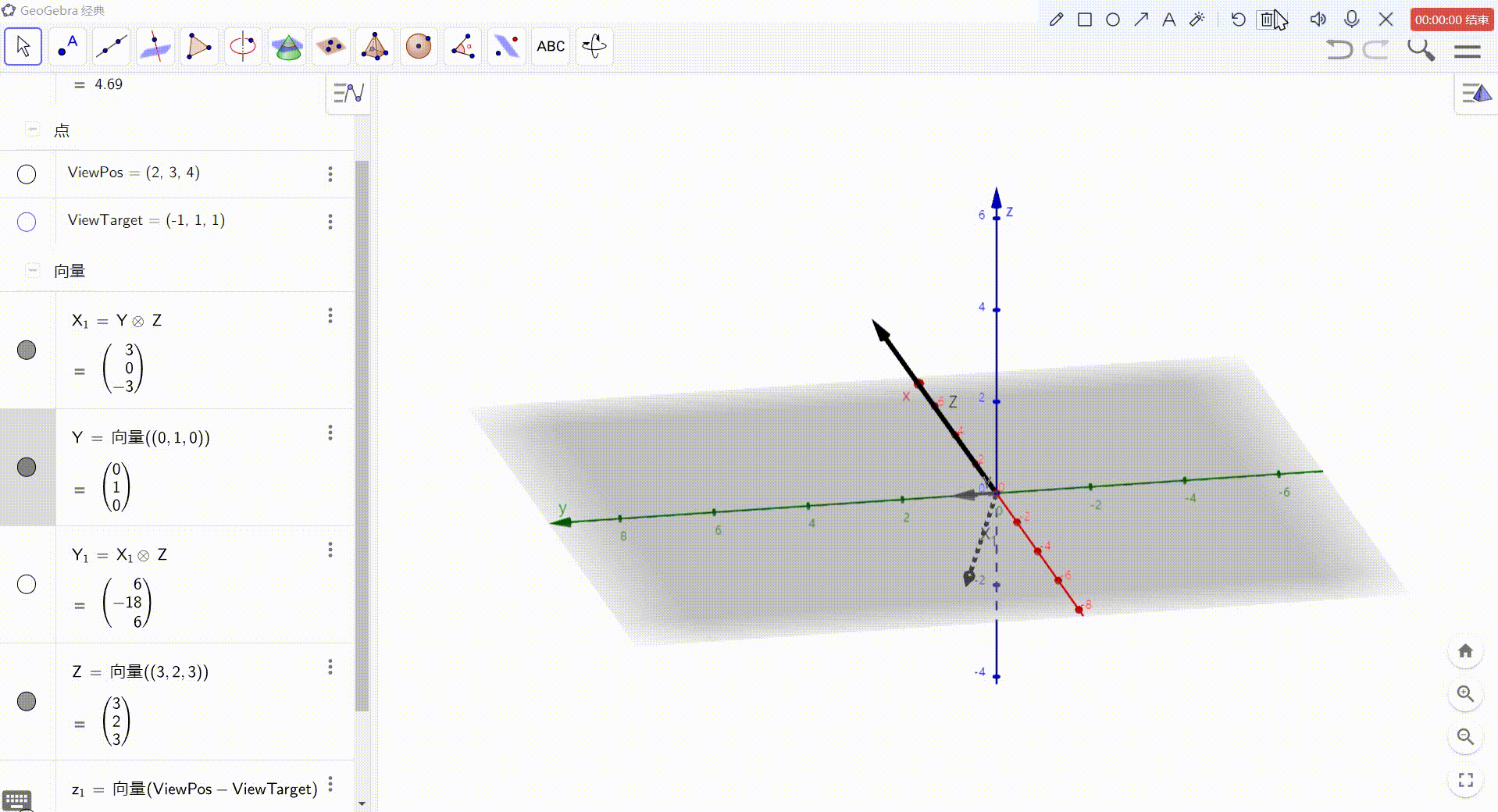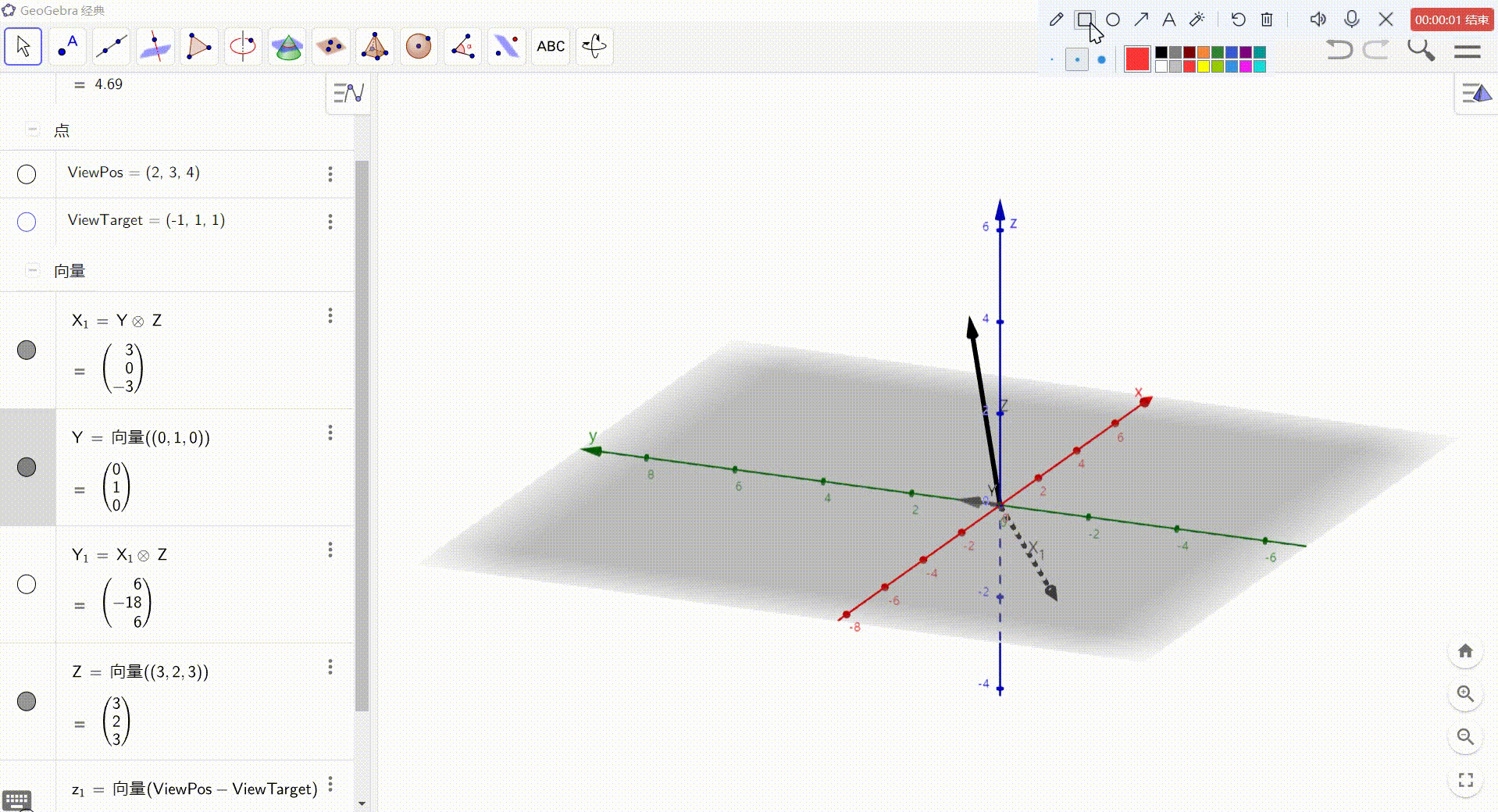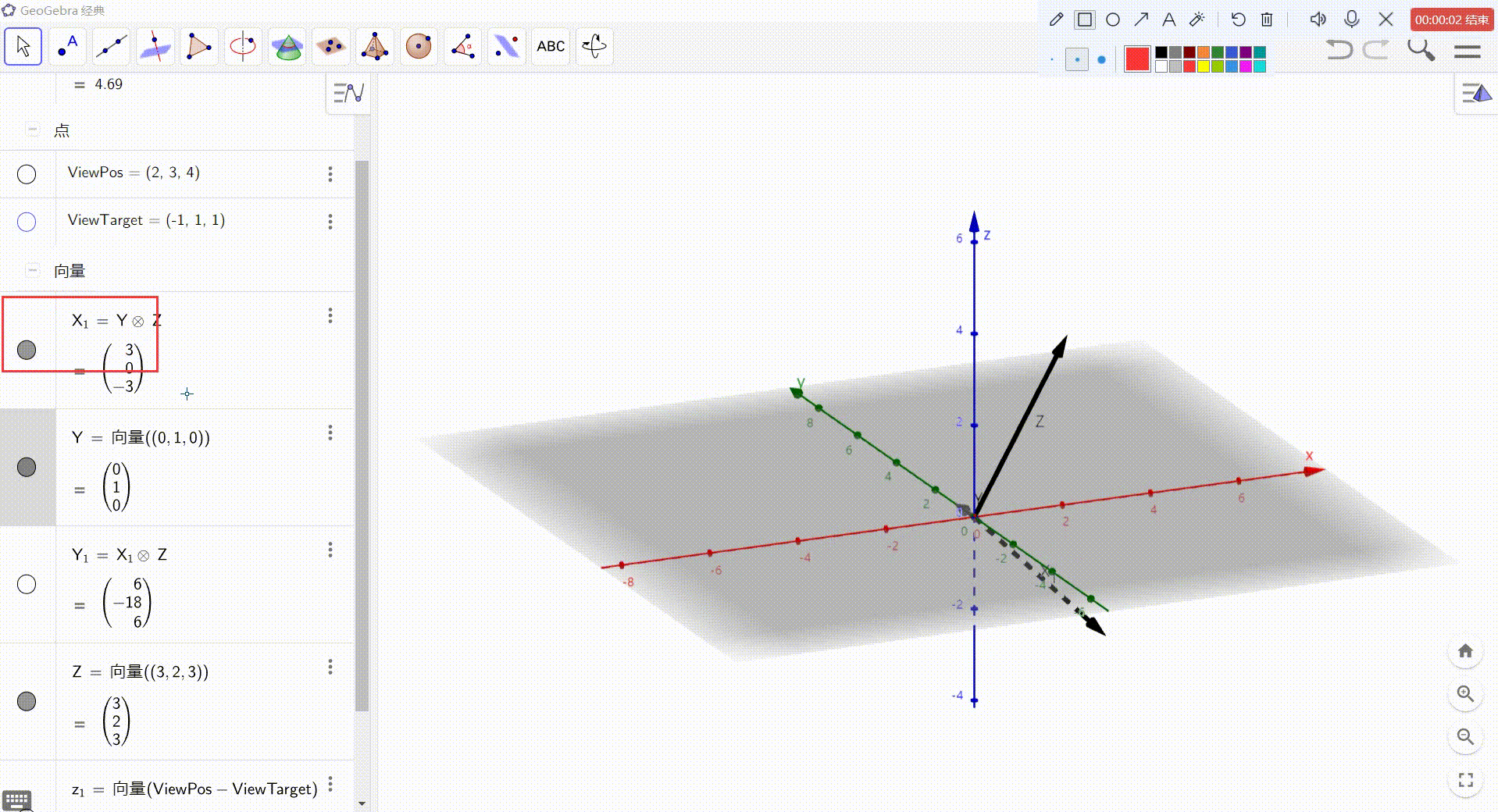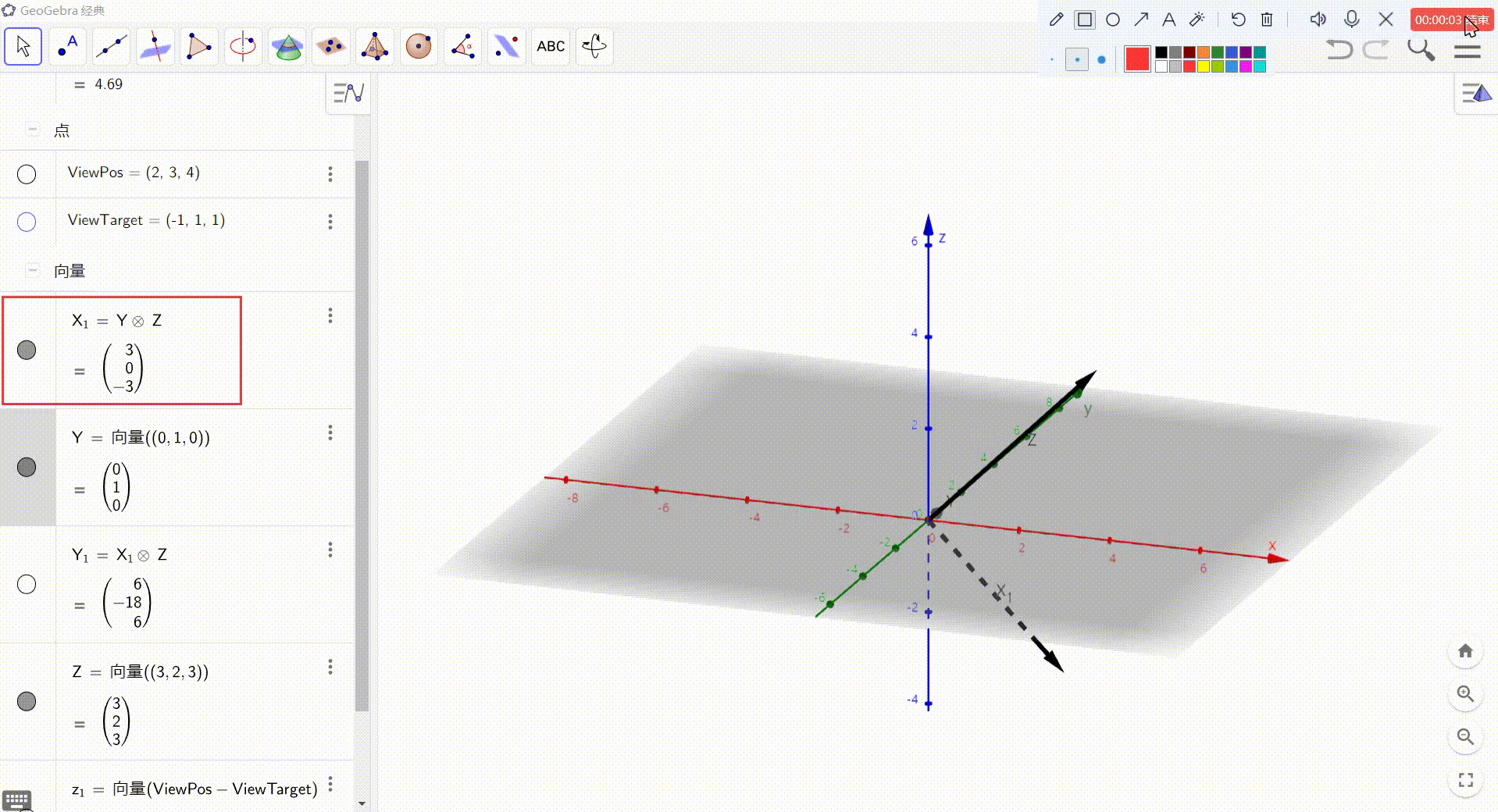
4、Y = X 与 Z 的叉积
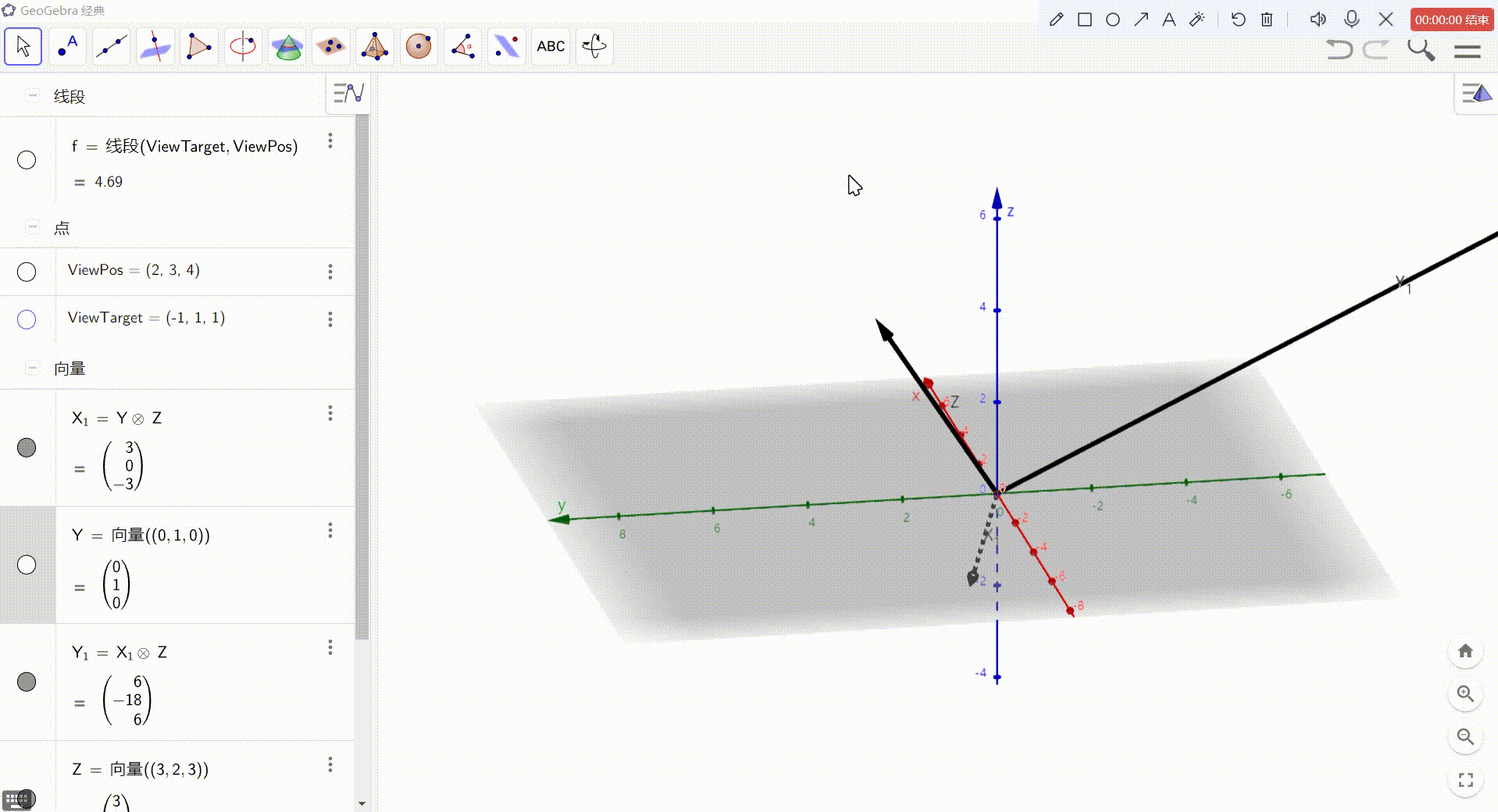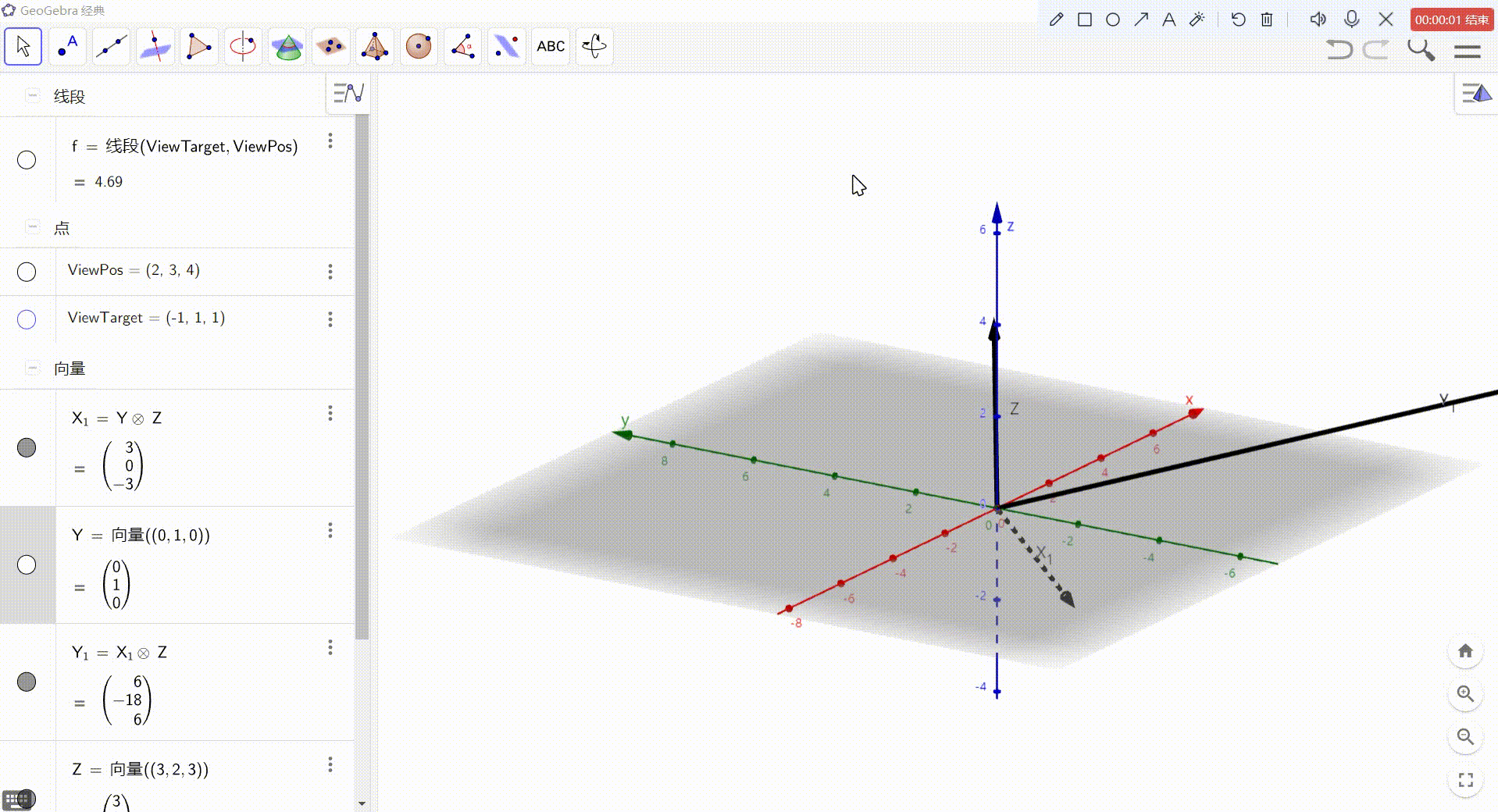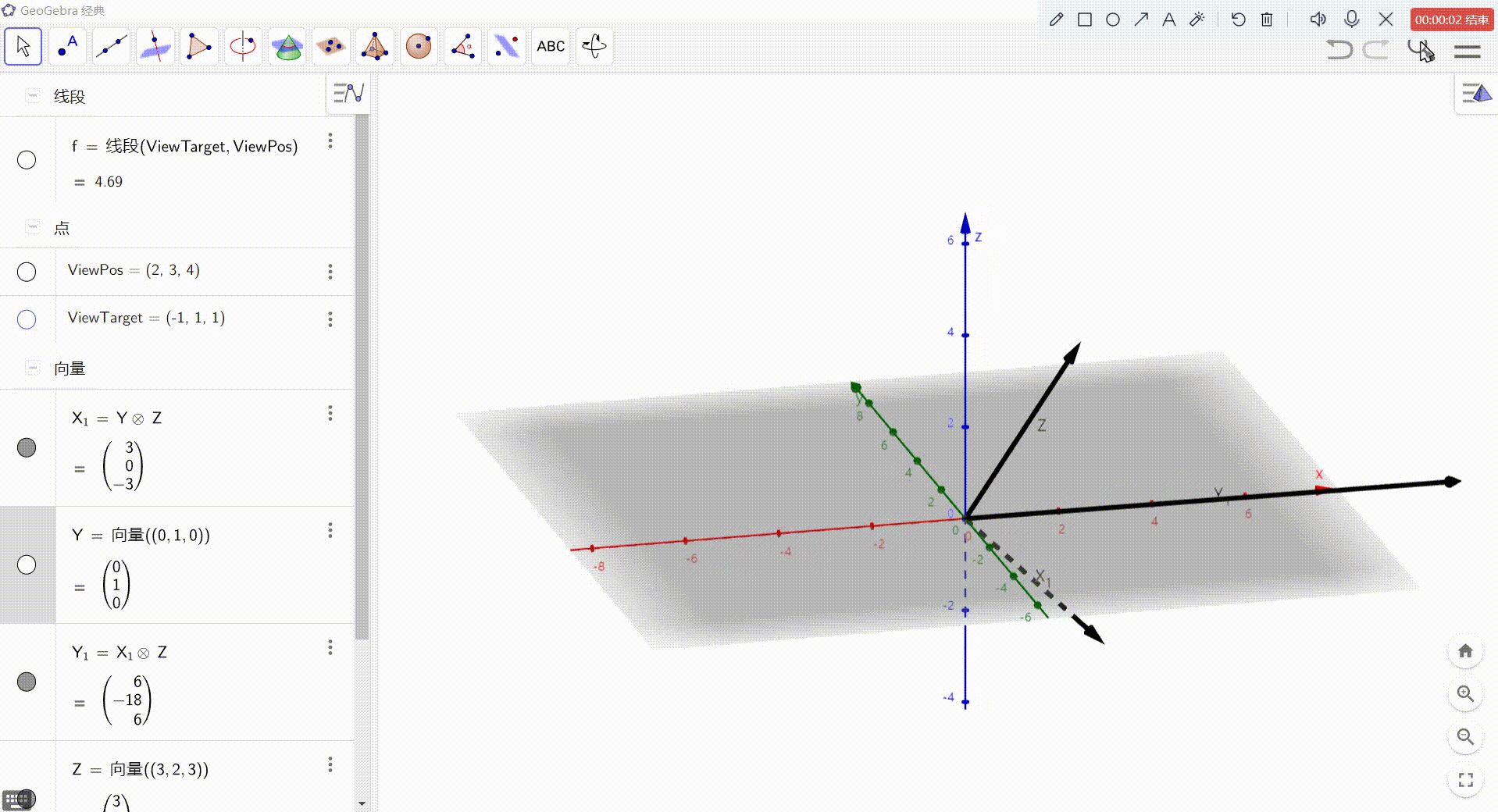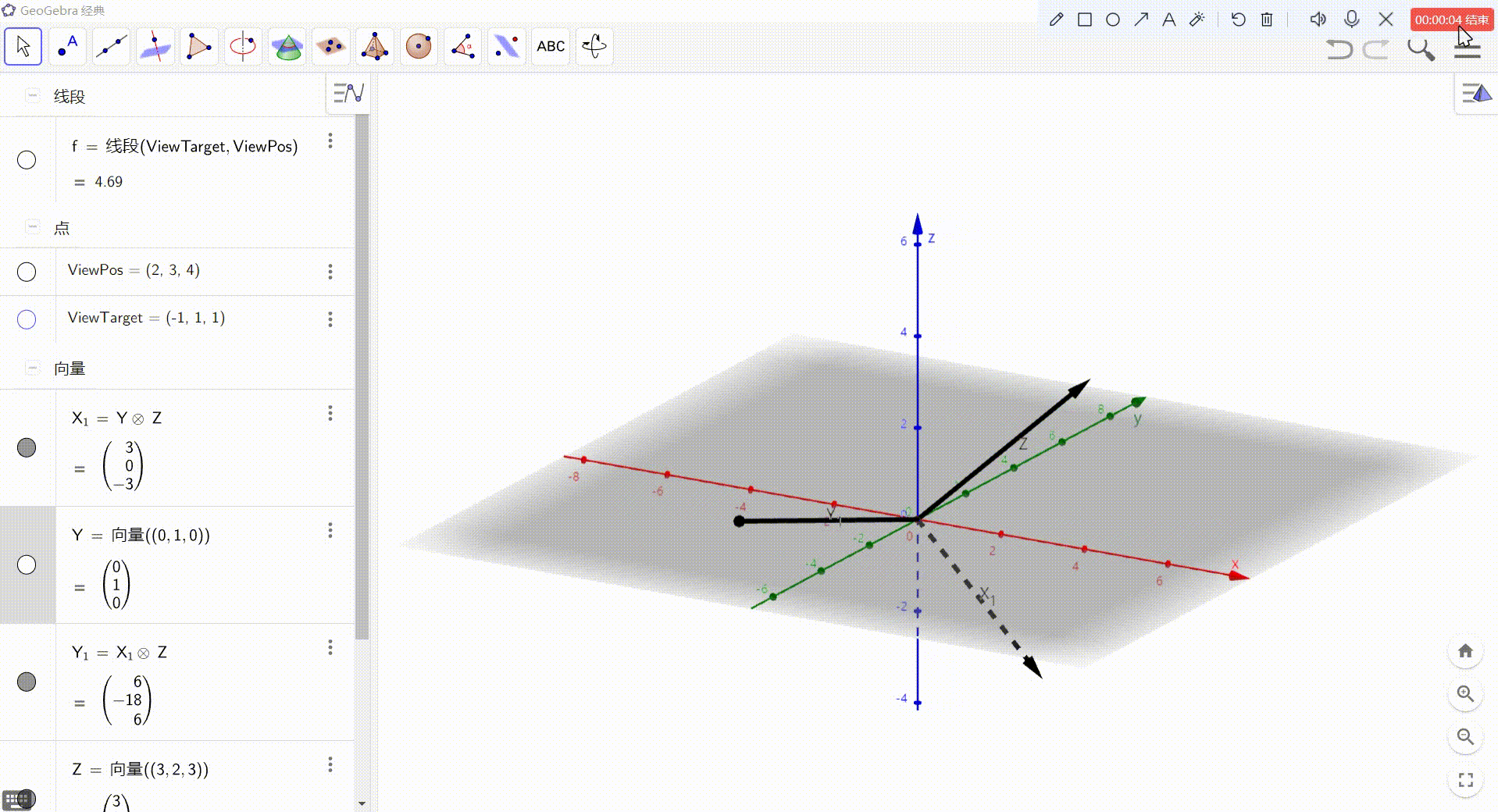
最后,得到的就是 视图空间坐标轴方向上的向量,归一化后即可作为基向量使用
三、求 [Vworld]T
1、求Vworld
- 把基向量一列一列的写来排列得到 Vworld
V w o r l d X x V w o r l d Y x V w o r l d Z x V w o r l d X y V w o r l d Y y V w o r l d Z y V w o r l d X z V w o r l d Y z V w o r l d Z z \begin{matrix} V~worldXx~&V~worldYx~&V~worldZx~\\ V~worldXy~&V~worldYy~&V~worldZy~\\ V~worldXz~&V~worldYz~&V~worldZz~\\ \end{matrix} V worldXx V worldXy V worldXz V worldYx V worldYy V worldYz V worldZx V worldZy V worldZz
2、求[Vworld]T
这里原本是求逆矩阵,但是基向量矩阵是正交矩阵,所以逆矩阵 = 转置矩阵
V w o r l d X x V w o r l d X y V w o r l d X z V w o r l d Y x V w o r l d Y y V w o r l d Y z V w o r l d Z x V w o r l d Z y V w o r l d Z z \begin{matrix} V~worldXx~&V~worldXy~&V~worldXz~\\ V~worldYx~&V~worldYy~&V~worldYz~\\ V~worldZx~&V~worldZy~&V~worldZz~\\ \end{matrix} V worldXx V worldYx V worldZx V worldXy V worldYy V worldZy V worldXz V worldYz V worldZz
四、求出最后在Unity中使用的公式
- Pview = [Vworld]T * Pworld
1、偏移坐标轴
在之前的步骤中,我们只完成坐标系的旋转转化。
但是,我们的 观察空间 和 世界空间 的原点不在同一地方。
所以,需要进行平移变换

2、把 平移的坐标 构建成之前文章中使用的 平移矩阵
1 0 0 − T x 0 1 0 − T y 0 0 1 − T z 0 0 0 1 \begin{matrix} 1&0&0&-T~x~\\ 0&1&0&-T~y~\\ 0&0&1&-T~z~\\ 0&0&0&1\\ \end{matrix} 100001000010−T x −T y −T z 1
- 则我们的公式会变成如下样子:
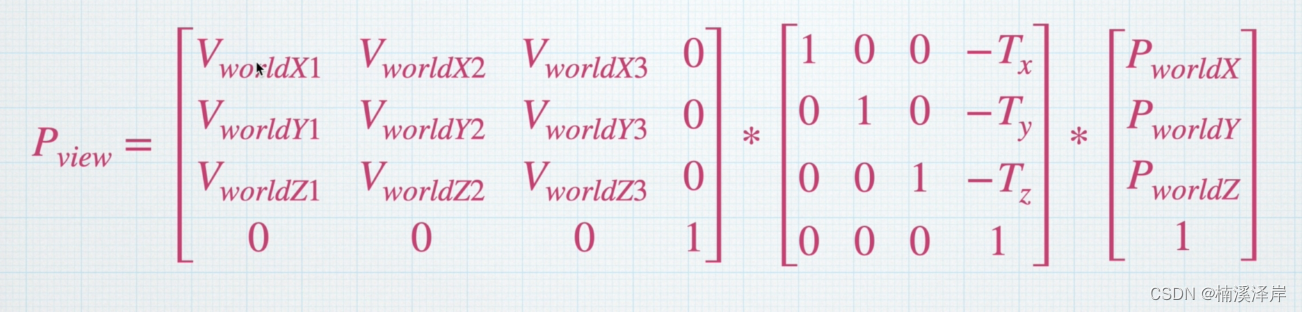
3、化简我们的矩阵
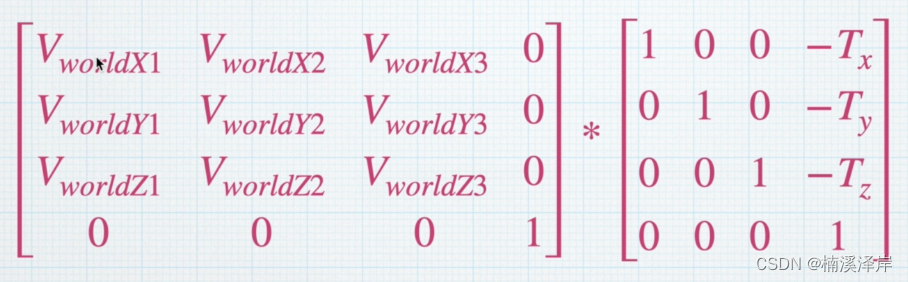
- 这两个矩阵相乘,最后的一列的结果,可以化简为:
− ( V w o r l d X d o t T ) − ( V w o r l d Y d o t T ) − ( V w o r l d Z d o t T ) 1 \begin{matrix} -(V~worldX~ dot T) \\ -(V~worldY~ dot T) \\ -(V~worldZ~ dot T) \\ 1\\ \end{matrix} −(V worldX dotT)−(V worldY dotT)−(V worldZ dotT)1
- 最后,公式化简为: