代码随想录算法训练营第四十二天 _ 动态规划_01背包问题、416.分割等和子集。
学习目标:
动态规划五部曲:
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录!
60天训练营打卡计划!
学习内容:
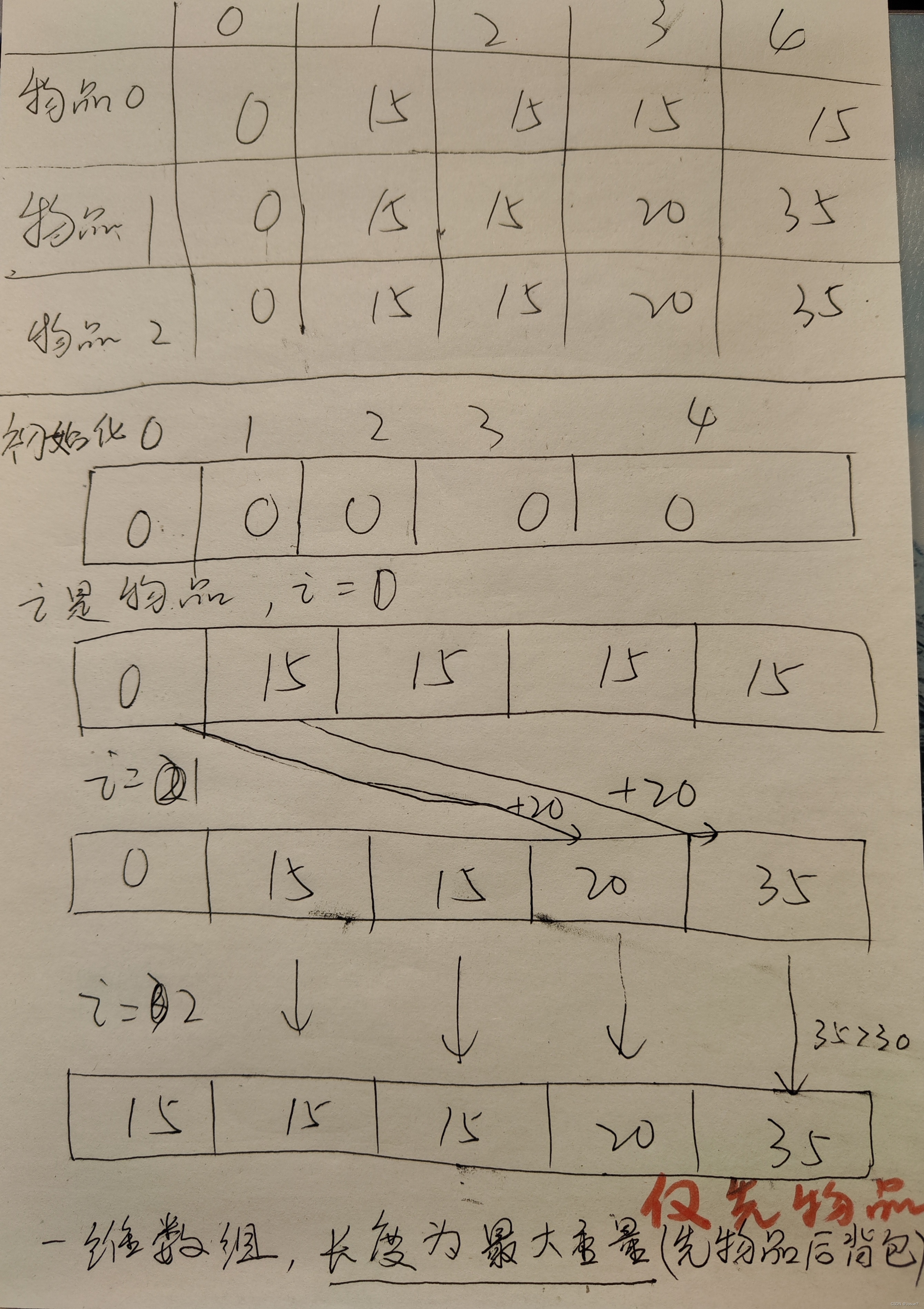
二维数组处理01背包问题
- 听起来思路很简单,但其实一点也不好实现。
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 任取[0, i]的物品后放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[i][j] = max(dp[i-1][j] , dp[i-1][ j - weight[i] ] + value[i])
Ⅰ 不放物品 i : dp[i-1][j]
Ⅱ 放物品 i : dp[i-1][j - weight[i]] + value[i]
③ dp数组如何初始化 : 按下表的第一行和第一列赋值,其中箭头都是继承来的值,画圈的表示自己取得了最大值。
④ 确定遍历顺序 : 先物品后背包(行) / 先背包后物品(列)
import java.util.Scanner;public class Main {public static void main(String[] args) {//m,n分别代表物品种类和背包容量int itemSize = 0,bagSize = 0;Scanner sc = new Scanner(System.in);//获取itemSize和bagSize的值itemSize = sc.nextInt();bagSize = sc.nextInt();//初始化对应的重量数组和价值数组int[] weight = new int[itemSize];int[] value = new int[itemSize];//这两个都是物品的属性,大小只和物品数量有关for(int i = 0;i < itemSize;i++){weight[i] = sc.nextInt();}for (int i = 0;i < itemSize;i++){value[i] = sc.nextInt();}// int[] weight = {1,3,4};// int[] value = {15,20,30};// int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){int itemSize = weight.length;// dp数组的含义是:在[0,i]件物品中选择是否放入背包 的 最大价值int[][] dp = new int[itemSize][bagSize+1];// 初始化dp数组,默认都为0.// 只放一件物品时的初始化for(int j = weight[0]; j < bagSize+1; j++){dp[0][j] = value[0];}// 正常的为dp数组赋值,依赖左上位置的其他的dp值for(int i = 1; i < itemSize; i++){// j是背包容量for(int j = 1; j < bagSize+1; j++){// 如果容量不够放入新的物品,则从上一行继承if(j < weight[i]) dp[i][j] = dp[i-1][j];// 如果容量可以放入新的物品,则从上一行的左侧继承elsedp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}System.out.println(dp[itemSize-1][bagSize]);// 打印dp数组// for (int i = 0; i < goods; i++) {// for (int j = 0; j <= bagSize; j++) {// System.out.print(dp[i][j] + "\t");// }// System.out.println("\n");// }}
}一维数组处理01背包问题
- 动态规划五步曲:
① 确定dp[j]的含义 : 任取物品放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[j] = max(dp[j] , dp[j - weight[i]] + value[i])
Ⅰ 不放物品 i : dp[j]
Ⅱ 放物品 i : dp[j - weight[i]] + value[i]
③ dp数组如何初始化 : 初始值全部附0,长度为容量的长度加1(j+1)
④ 确定遍历顺序 : 必须先物品后背包(行),且便利背包大小时,必须使用倒序的顺序遍历。(为了防止一个物品被使用多次,倒叙遍历时相同的物品仅能被取用一次)
import java.util.Scanner;public class Main {public static void main(String[] args) {//m,n分别代表物品种类和背包容量int itemSize = 0,bagSize = 0;Scanner sc = new Scanner(System.in);//获取itemSize和bagSize的值itemSize = sc.nextInt();bagSize = sc.nextInt();//初始化对应的重量数组和价值数组int[] weight = new int[itemSize];int[] value = new int[itemSize];//这两个都是物品的属性,大小只和物品数量有关for(int i = 0;i < itemSize;i++){weight[i] = sc.nextInt();}for (int i = 0;i < itemSize;i++){value[i] = sc.nextInt();}// int[] weight = {1,3,4};// int[] value = {15,20,30};// int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp一维数组int goods = weight.length; // 获取物品的数量int[] dp = new int[bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0// 填充dp数组for (int i = 0; i < goods; i++) {// 必须使用倒叙遍历背包大小for (int j = bagSize; j > 0; j--) {// 防止越界错误if (j < weight[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j] , dp[j-weight[i]] + value[i]);}}}System.out.print(dp[bagSize]);// 打印dp数组// System.out.print(dp[goods-1][bagSize] + "\n");// for (int i = 0; i < goods; i++) {// for (int j = 0; j <= bagSize; j++) {// System.out.print(dp[i][j] + "\t");// }// System.out.println("\n");// }}
}
416.分割等和子集
该题目可以等效为一个重量和价值相等的01背包问题,所以使用一维的数组就可。
- 因为题目问的是可不可以分为两个等和子集,没有问具体应该怎么分。
- 动态规划五步曲:
① 确定dp[j]的含义 : 容量为j的背包的最大价值
② 求递推公式 : dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
③ dp数组如何初始化 : 全部为零
④ 确定遍历顺序 : 先遍历物品,再倒叙遍历背包。 - 实现的特别巧妙,将该问题视为一个重量和价值相等的01背包问题,将目标和作为背包的重量,只要背包重量最大时能达到目标和的价值,即找到了一组数满足目标,那么此时该数组就可以分为等和的子集。
class Solution {public boolean canPartition(int[] nums) {int total = 0;for(int num :nums){total += num;}if(total % 2 == 1) return false;// target就是背包的最大重量int target = total / 2;int[] dp = new int[target+1];// 初始化:数组定义的时候已经被全部赋值0// 递推函数for(int i = 0; i < nums.length; i++){for(int j = target; j >= 0; j--){if(j < nums[i]) dp[j] = dp[j];else{dp[j] = Math.max(dp[j], dp[j - nums[i]]+nums[i]);}}}// 因为target是整除2得到的,所以只要能找到一组数使其和为target// 剩下的数的和也是targetif(dp[target] == target) return true;else return false;}
}
学习时间:
- 上午两个半小时,整理文档半小时。
