当前位置： 首页 > news >正文

【数据结构】堆的向上调整和向下调整以及相关方法

news 2025/7/18 18:35:39

在这里插入图片描述

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃

文章目录

  • 一、堆的概念
  • 二、堆的性质
  • 三、堆的分类
    • 1.大根堆
    • 2.小根堆
  • 四、说明
  • 五、堆的结构
  • 🚩六、堆的向上调整
    • 1.图示
    • 2.代码实现
    • ⌚️3.时间复杂度分析
  • 📌七、堆的向下调整
    • 1.思路：
    • 2.代码实现
    • ⌚️3.时间复杂度分析
  • 八、删除根
    • 1.思路：
    • 2.代码实现
    • ⌚️3.时间复杂度分析
  • 九、创建堆
    • 1.思路：
    • 2.代码实现
  • 十、所有方法实现汇总

一、堆的概念

堆(Heap)是计算机科学中一类特殊的数据结构的统称。如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1， 2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。除了最后一层以外上面的节点但是非空的，最后一层节点是从左到右依次排布的）

二、堆的性质

🔸 非线性，完全二叉树。适合用数组存储。
🔸堆是无序的，也就是左右可以互换
🔸最值总在 0 号位
根据这个特点我们就可以做很多事情，比如TopK问题 (在一堆数据里面找到前 K 个最大 / 最小的数).
比如点餐软件中有上千家店铺，我想选出该地区好评最多的十家川菜店，我们不用对所有数据排序，只需要取出前 K 个最大 / 最小数据。使用堆排序效率也更高。

三、堆的分类

1.大根堆 2.小根堆

1.大根堆

定义：树中的任意一个双亲节点都大于等于孩子节点。
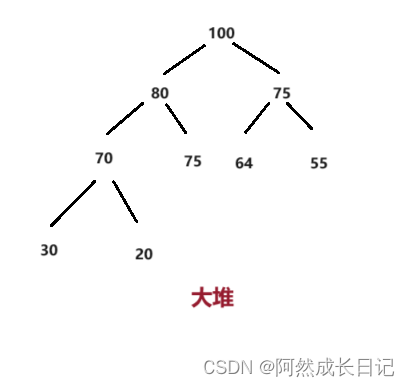
在这里插入图片描述

2.小根堆

定义：树中的任意一个双亲节点都小于等于孩子节点。

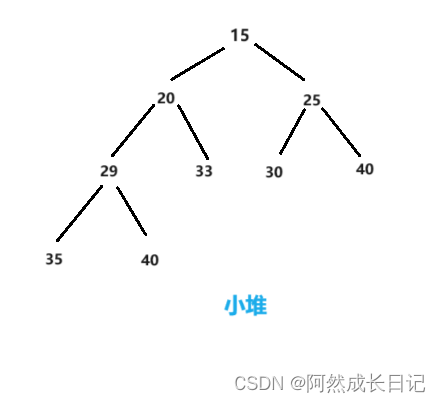
在这里插入图片描述

四、说明

以下的方法均以小堆来推理，如果想实现大堆，则修改【<】符号等方式实现。

五、堆的结构

typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

🚩六、堆的向上调整

向上调整的前提是，调整位置之前必须是堆。如果目的是调成小堆，则要保证调整位置之前是小堆；如果目的是调成大堆，则要保证调整位置之前是大堆。

1.图示

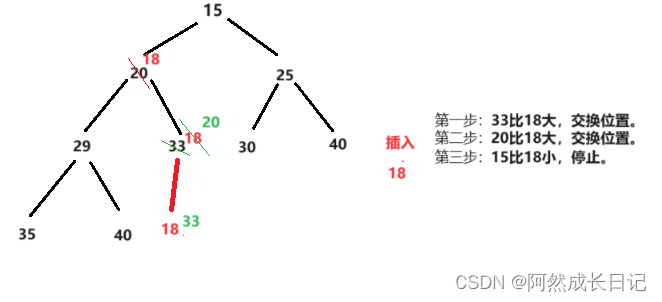
在这里插入图片描述

2.代码实现

//向上调整
void AdjustUp(HPDataType* a, int child)
{//传入数组，child为孩子节点下标int parent = (child - 1) / 2;//当一直交换到根，停止while (child>0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsereturn;}
}

⌚️3.时间复杂度分析

时间复杂度：O（logN）
最坏情况：调整到根;
最好情况：不用调整，

📌七、堆的向下调整

向下调整的前提是，左右子树必须是小堆或者大堆。

1.思路：

如图：
此案例是要调整根节点40开始向下调整，首先确保根节点的左右子树是小堆（由图得成立）。
1.parent的两个孩子进行比较，选出小的。
2.进行交换
3.child>n结束
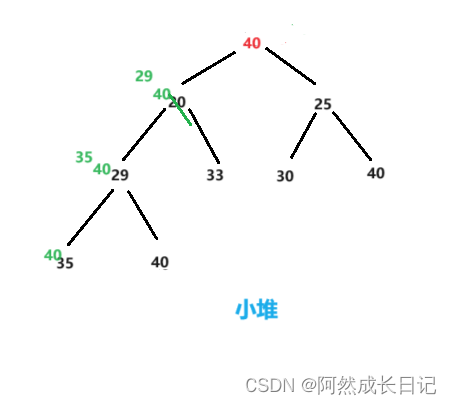
在这里插入图片描述

2.代码实现

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后，也就是数组的最后一个位置while (parent<n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}

⌚️3.时间复杂度分析

时间复杂度：O（logN）
最坏情况：调整到根;
最好情况：不用调整，

八、删除根

1.思路：

1.先将根与最后一个节点交换，
2.删除最后一个节点；
3.进行向下调整。

在这里插入图片描述

2.代码实现

void HeapPop(HP* p)
{assert(p);assert(p->size > 0);Swap(&p->a[0], &p->a[p->size - 1]);--p->size;AdjustDown(p->a, p->size, 0);
}

⌚️3.时间复杂度分析

时间复杂度：O:N(logN)

九、创建堆

创建堆的思路可以通过向上调整，也可通过向下调整。这里讲通过向上调整建立堆。
由于我的AdjustUp函数是用来调整小堆的，所以，这里创建的也是小堆。

1.思路：

传入参数
a：数组，n：是数组元素个数
1.为p->a开辟n个空间；
2.利用memcpy函数，把数组a复制到p->a中
3.在使用AdjustUp调整，从1-n-1逐步向下延伸；
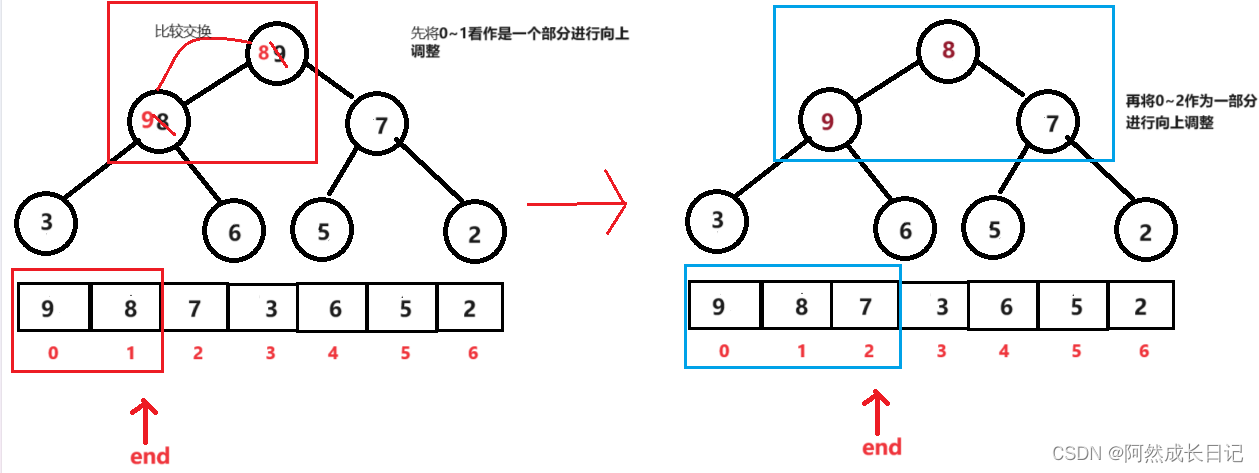
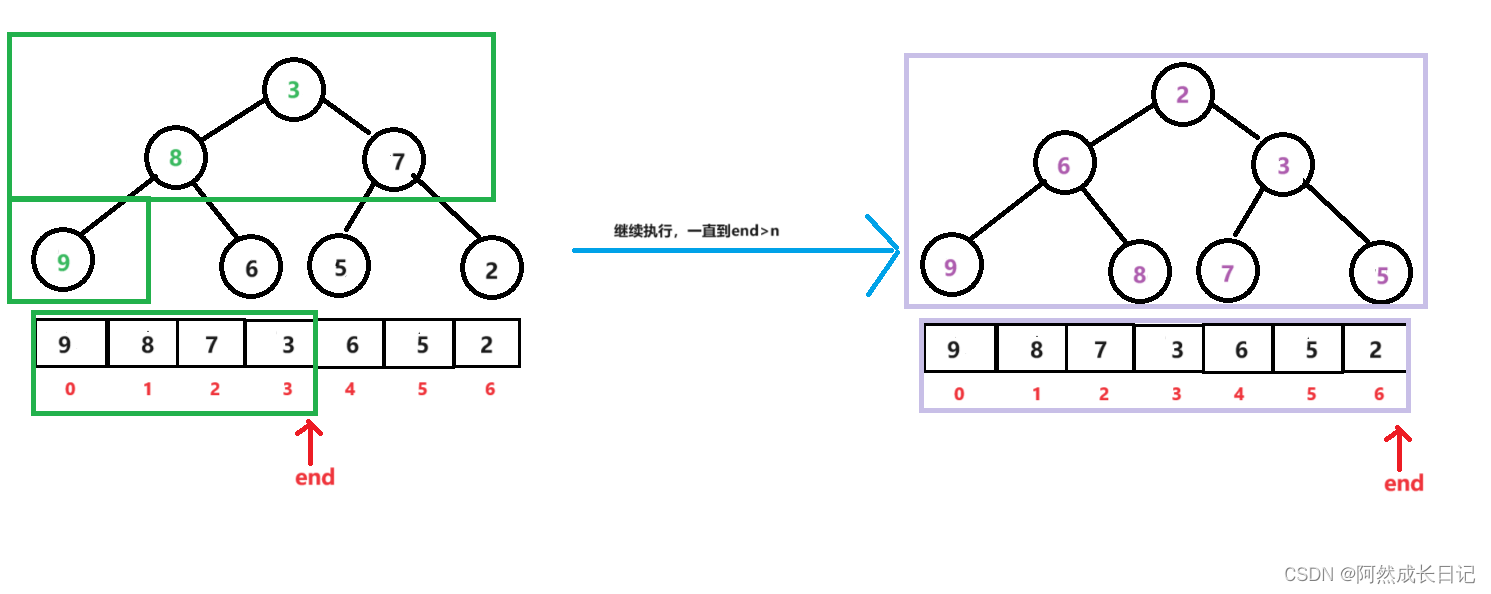
在这里插入图片描述
在这里插入图片描述

2.代码实现

//建立小堆
void HeapInitArray(HP* p, int* a, int n)
{//a：数组，n：是数组元素个数assert(p);assert(a);p->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (p->a == NULL){perror("malloc fail");exit(-1);}p->size = n;p->capacity = n;//把传入数组a复制到p->a中memcpy(p->a, a, sizeof(HPDataType) * n);// 向上调整，调整成一个小堆for (int i = 1; i < n; i++){AdjustUp(p->a, i);}
}

十、所有方法实现汇总

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"//初始化
void HeapInit(HP* p)
{assert(p);p->a = NULL;p->size = 0;p->capacity = 0;
}//销毁
void HeapDestroy(HP* p)
{assert(p);free(p->a);p->a = NULL;p->size = p->capacity = 0;
}//插入数据
void HeapPush(HP* p, HPDataType x)
{//从最后一个位置插入assert(p);//扩容if (p->capacity == p->size){//如果刚开始数组为空，就开辟4个空间。如果不为空，以后每次扩大2倍。int newcapacity = p->capacity==0 ? 4 : p->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(p->a, sizeof(HPDataType) * p->capacity);if (tmp == NULL){perror("realloc fial\n");exit(-1);}p->a = tmp;p->capacity = newcapacity;}p->a[p->size] = x;p->size++;AdjustUp(p->a, p->size-1);
}//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{//传入数组，child为孩子节点下标int parent = (child - 1) / 2;//当一直交换到根，停止while (child>0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsereturn;}
}//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后，也就是数组的最后一个位置while (parent<n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}//打印二叉树
void HeapPrint(HP* php)
{assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}//建立小堆
void HeapInitArray(HP* p, int* a, int n)
{//a：数组，n：是数组元素个数assert(p);assert(a);p->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (p->a == NULL){perror("malloc fail");exit(-1);}p->size = n;p->capacity = n;//把传入数组a复制到p->a中memcpy(p->a, a, sizeof(HPDataType) * n);// 向上调整，调整成一个小堆for (int i = 1; i < n; i++){AdjustUp(p->a, i);}
}//删除根
void HeapPop(HP* p)
{assert(p);assert(p->size > 0);Swap(&p->a[0], &p->a[p->size - 1]);--p->size;AdjustDown(p->a, p->size, 0);
}
//获取根
HPDataType HeapTop(HP* p)
{assert(p);assert(p->size > 0);return p->a[0];
}//判空
bool HeapEmpty(HP* p)
{assert(p);return p->size == 0;
}
http://www.lryc.cn/news/166759.html

相关文章：

  • 【蓝桥杯选拔赛真题60】Scratch旋转风车 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
  • JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析
  • 微信小程序的图书馆图书借阅 座位预约系统 读者端设计与实现
  • 在阿里云 linux 服务器上查看当前服务器的Nginx配置信息
  • 专业招投标书翻译怎样做比较好
  • 算法总结10 线段树
  • 518抽奖软件，支持按人像照片抽奖
  • 数字IC笔试面试题之--时钟偏斜（skew）与抖动（jitter）
  • 免费api接口：物流api,企业工商查询api,游戏api。。。
  • 第二十八章 Classes - 引用其他类的方法
  • Android 中集成 TensorFlow Lite图片识别
  • NSSCTF之Misc篇刷题记录（16）
  • 域名解析--nslookup和dig
  • EXCEL如何把一个单元格内的文本和数字分开？例如：龚龚15565 = 龚龚 15565
  • uniapp抽取组件绑定事件中箭头函数含花括号无法解析
  • 猫头虎博主第四期赠书活动：《精通Go语言：(第2版) 》
  • 【学习总结】EasyExcel合并同列不同行，表格数据相同的行
  • Tokenview X-ray功能：深入探索EVM系列浏览器的全新视角
  • 【洛谷 P1364】医院设置 题解（图论+深度优先搜索）
  • 【Java基础】- RMI原理和使用详解
  • 无水印免费4K视频素材网站 可商用-Free Stock Video
  • kubesphere中间件部署
  • 使用 AWS S3 SDK 访问 COS-腾讯云国际站代充
  • c语言每日一练(15)
  • 如何利用软文推广进行SEO优化（打造优质软文，提升网站排名）
  • Java线程池ExecutorService和Executors应用(Spring Boot微服务)
  • 机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)
  • Django系列：Django简介与MTV架构体系概述
  • 锐捷交换机WEB管理系统EXCU_SHELL密码信息泄漏漏洞
  • 线性代数(六) 线性变换