算法总结10 线段树
算法总结10 线段树
- 线段树
- 2569. 更新数组后处理求和查询
线段树
有一个数组,我们要:
- 更新数组的值(例如:都加上一个数,把子数组内的元素取反)
- 查询一个子数组的值(例如:求和,求最大值,求最小值)
更新于查询,如果暴力去做,每个操作都是O(n)的。所以我们需要提升效率。
两大思想:
- 挑选O(n)个特殊区间,使得任意一个区间,可以拆分为O(logn)个特殊区间(用最近公共祖先来思考)
O(n)<=4n
挑选O(n)个特殊区间:build
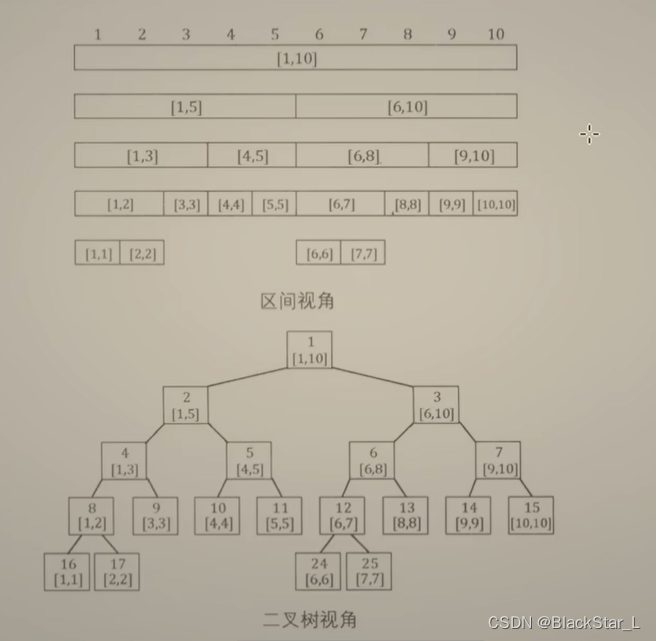
- lazy 更新 / 延迟更新
lazy tag:用一个数组维护每个区间需要更新的值
如果说这个值 = 0,表示不需要更新
如果这个值 != 0,表示更新操作在这个区间停住了,不继续地柜更新子区间了
如果后面又来了一个更新,破坏了于lazy tag的区间,那么这个区间就得继续递归更新了
模板:
class Solution:def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:n = len(nums1)todo = [0] * (4 * n)def build(o: int, l: int, r: int) -> None:if l == r:# ...returnm = (l + r) // 2build(o * 2, l, m)build(o * 2 + 1, m + 1, r)# 维护...# 更新 [L,R]def update(o: int, l: int, r: int, L: int, R: int, add: int) -> None:if L <= l and r <= R:# 更新 ...todo[o] += add # 不再继续递归更新了return m = (l + r)//2# 需要继续递归,就把 todo[o] 的内容传下去(给左右儿子)if todo[o] != 0:todo[o*2] += todo[o]todo[o*2+1] += todo[o]todo[o] = 0if m >= L:update(o*2, l, m, L, R, add)if m < R:update(o*2+1, m+1, r, L, R, add)# 维护 ...
2569. 更新数组后处理求和查询
2569. 更新数组后处理求和查询
class Solution:def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:n = len(nums1)cnt = [0]*(4*n)todo = [False]*(4*n)# 求非叶子节点def maintain(o):cnt[o] = cnt[o*2] + cnt[o*2+1]# 进行01翻转def do(o, l, r):# 翻转cnt[o] = r-l+1-cnt[o]# 翻一次为反,翻两次为正todo[o] = not todo[o]# 初始化线段树def build(o, l, r):# 叶子结点if l == r:cnt[o] = nums1[l-1]return# 非叶子结点 mid = (l+r)//2build(o*2, l, mid)build(o*2+1, mid+1, r)maintain(o)def update(o, l, r, L, R):if L<=l and r<=R:do(o, l, r)returnmid = (l+r)//2# 先将当前节点的值传给子节点if todo[o]:do(o*2, l, mid)do(o*2+1, mid+1, r)todo[o]=False# 待翻转的区间有分歧,二分处理if mid>=L:update(o*2, l, mid, L, R)if mid<R:update(o*2+1,mid+1, r, L, R)# 反转后更新节点的值maintain(o)# 初始化build(1, 1, n)# 记录答案,求和(每次都是在sum(nums2)的基础上增加值l*cnt[1])ans, s = [], sum(nums2)for op, l, r in queries:if op == 1:# 每次都从整个范围,将l+1和r+1的范围进行翻转(索引从1开始)update(1, 1, n, l+1, r+1)elif op == 2:# cnt从1开始s += l*cnt[1]else:ans.append(s)return ans参考
