11 Advanced CNN

课程来源： 链接

对于前篇中所提到问题，设计出的是一种类似于LeNet5的线性结构，而对于大多数问题，简单的卷积神经网络无法满足需求，因此需要对其进行改进，使之成为一种更加复杂的网络。

GoogLeNet

GoogLeNet包括卷积（Convolution），池化（Pooling）、全连接（Softmax）以及连接（Other）四个部分。

而为了减少代码的冗余，将由以上四个模块所组成的相同的部分，封装成一个类/函数，在GoogLeNet中，这样的部分被称为Inception Module。

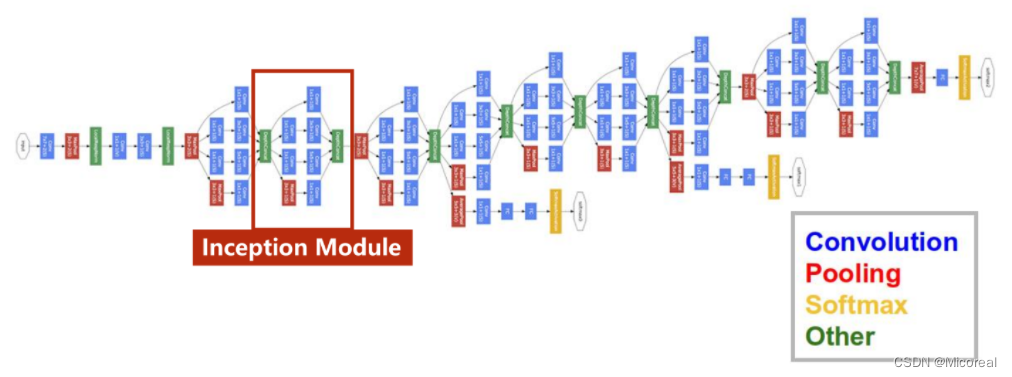
Inception Module

实际上Inception Module以及GoogLeNet自身只是一种基础的网络结构，他的出现是为了解决构造网络时的部分超参数难以确定的问题。

以卷积核大小(kernel_size)为例，虽然无法具体确定某问题中所应使用的卷积核的大小。但是往往可以有几种备选方案，因此在这个过程中，可以利用这样的网络结构，来将所有的备选方案进行计算，并在后续计算过程中增大最佳方案的权重，以此来达到确定超参数以及训练网络的目的。

其中的具体成分可以根据问题进行调整，本文中所详细介绍的Inception Module也仅用作参考。

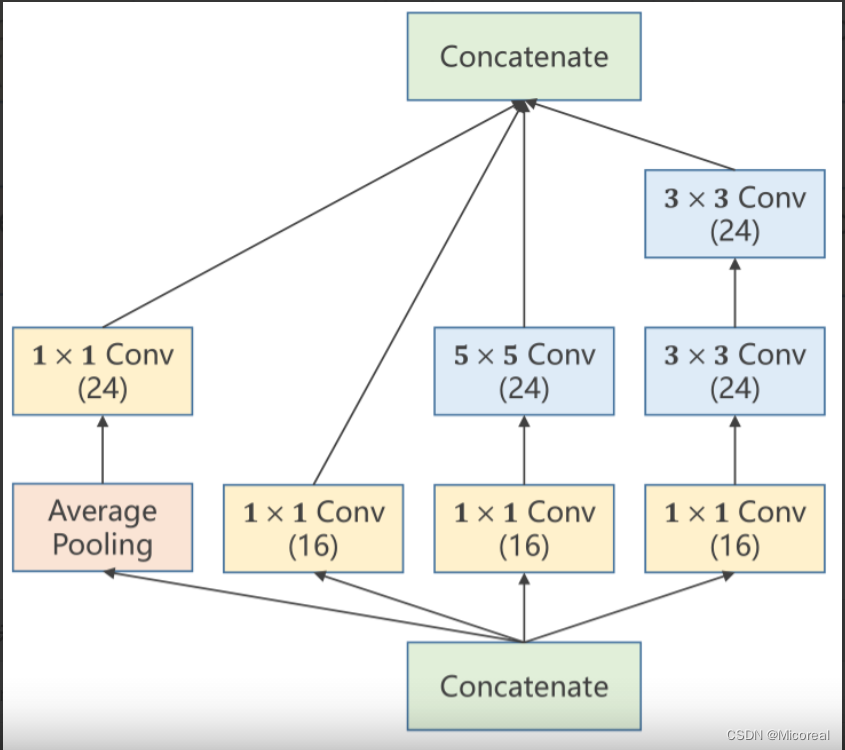
在上述四个路径（四种方法）中，最终的输出图必须仍然保持相同的W（图像宽度）以及H（图像高度），不然无法再次进行拼接传输到下一层模块中。

1x1 Conv

在$1\times 1$卷积中，每个通道的每个像素需要与卷积中的权重进行计算，得到每个通道的对应输出，再进行求和得到一个单通道的总输出，以达到信息融合的目的。即将同一像素位置的多个通道信息整合在同位置的单通道上。

若需要得到多通道的总输出，以M个通道为例，则需M组的卷积进行计算再进行堆叠拼接。此处和前篇中的多通道卷积是一样的。

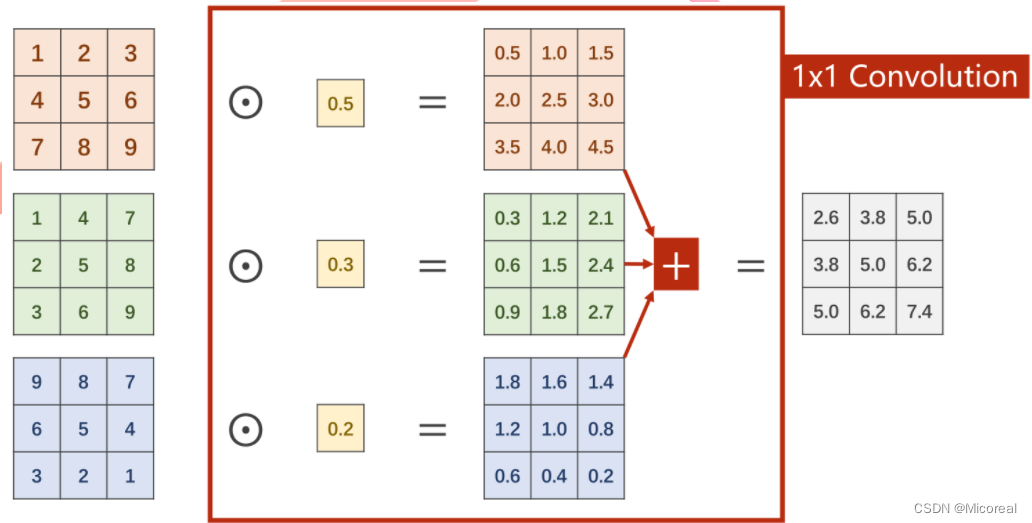
计算效果

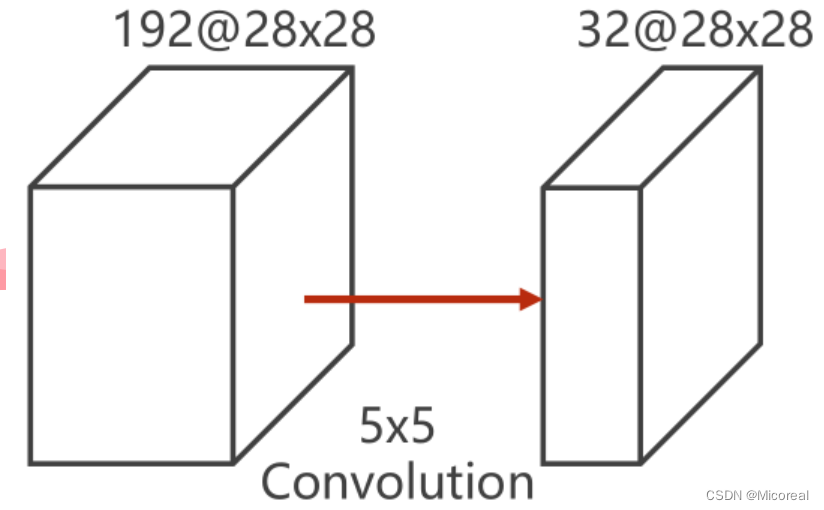
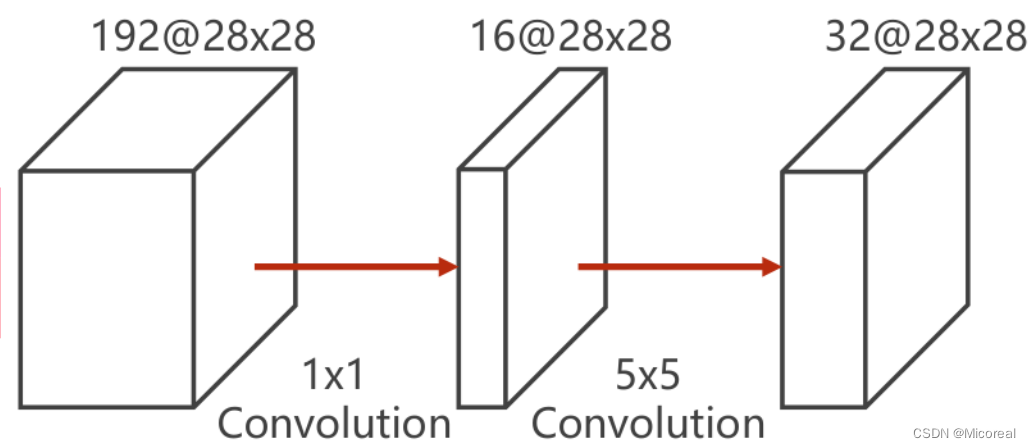
为说明$1\times 1$ 卷积的效用，举例原图为$192\times 28\times 28$的图像，即192个通道，宽高皆为28的图像。输出为$32\times 28\times 28$的图像，即32个通道，宽高皆为28的图像。为保证前后大小一致，需要使每个像素都在卷积核的中央，即对原图进行padding操作。
若单纯利用一个$5\times 5$的卷积核进行卷积，此时对于每一次卷积，需要计算$5^2$次，对于每一个通道需要计算$28^2$次卷积，而原图中一共有128个通道，则需要再计算128轮次，此时得到一个单通道的$28\times 28$的的输出，因此需要重复上述计算32次，才能得到一个$32\times 28\times 28$的输出。
即需要计算一亿两千万次以上
$$5^2\times 28^2\times 192\times 32=120422400$$

而对于添加$1\times 1$卷积核的结构，按照上述过程进行计算，仅需要计算一千两百万次左右，整体耗费已经缩减到了原先的十分之一。
$$1^2\times 28^2\times 192\times 16+5^2\times 28^2\times 16\times 16=12433648$$

代码实现

为了便于代码说明，此处将原Inception Module模块计算图进行了标注，并对模块中的每一个标注进行单独的代码补充，详解写在代码中

其中主要分为两部分，即对于每一条计算路径上的每一个子模块都包括init定义以及forward计算两部分组成。

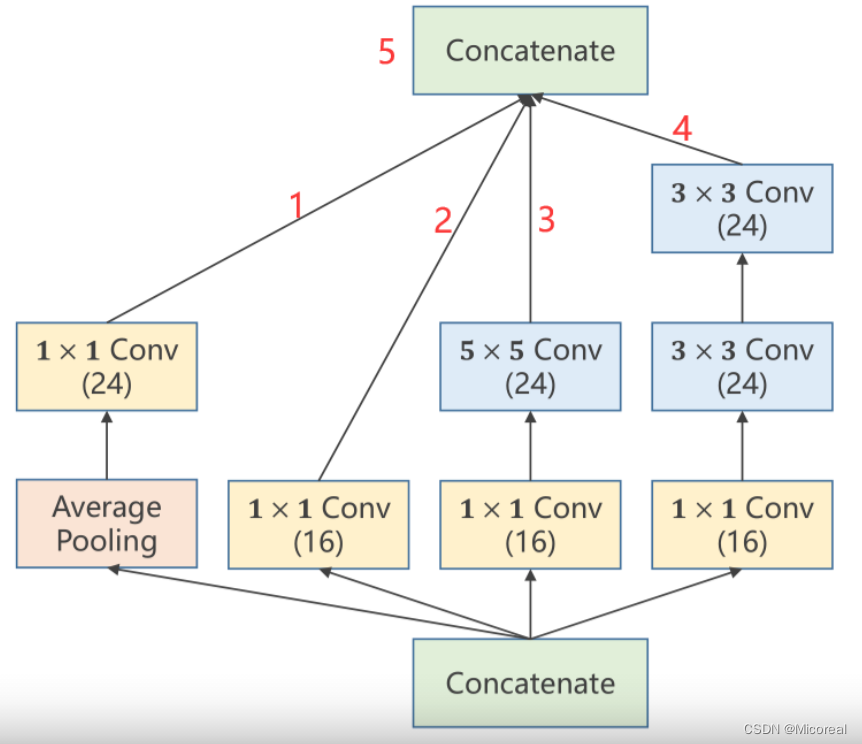
第一部分是由一个均值池化层以及一个输出通道为24的$1\times 1$的卷积构成

#init内定义1x1卷积（输入通道 输出通道 卷积核大小）
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)#forward内的方法
#avg_pool2d->均值池化函数 stride以及padding需要手动设置以保持图像的宽度和高度不变
branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
#括号内branch_pool的是池化后的结果，括号外的branch_pool是定义的1x1卷积，赋值给对象branch_pool
branch_pool = self.branch_pool(branch_pool)

第二部分是一个输出通道为16的单一的$1\times 1$的卷积

#init中的定义
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)#将元数据直接用于卷积
branch1x1 = self.branch1x1(x)

第三部分包括一个输出通道为16的$1\times 1$的卷积，以及一个输出通道为24的$5\times 5$的卷积

#init定义
self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
#设置padding是为了保持图像宽高不变
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)#按照计算图的顺序进行forward嵌套运算
branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)

第四部分包括一个输出通道为16的$1\times 1$的卷积和两个输出通道为24的$3\times 3$的卷积

self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)branch3x3 = self.branch5x5_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)

此时经过计算后，会得到各自通道数目不一但图像大小一致的四组图，再利用Concatenate按通道维度方向进行拼接即可得到输出图像

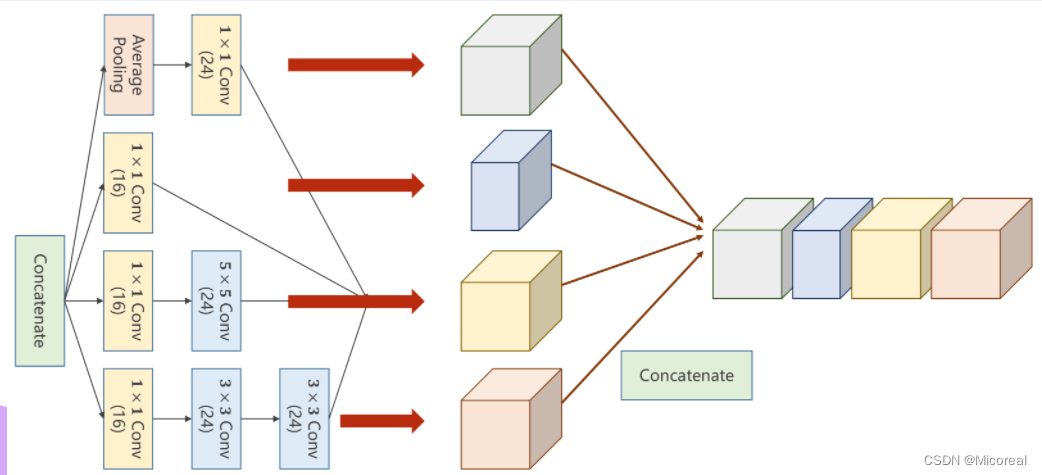
这一过程的步骤如下。

outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
#dim=1 意味着按下标为1的维度方向拼接，在图像中即暗指通道（B,C,W,H）
return torch.cat(outputs, dim=1)

代码整理：

class InceptionA(nn.Module):#仅是一个模块，其中的输入通道数并不能够指明def __init__(self, in_channels):super(InceptionA,self).__init__()self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):branch1x1 = self.branch1x1(x)branch5x5 = self.branch5x5_1(x)branch5x5 = self.branch5x5_2(branch5x5)branch3x3 = self.branch5x5_1(x)branch3x3 = self.branch3x3_2(branch3x3)branch3x3 = self.branch3x3_3(branch3x3)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)branch_pool = self.branch_pool(branch_pool)outputs = [branch1x1, branch5x5, branch3x3, branch_pool]return torch.cat(outputs, dim=1)class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)# 在Inception的定义中，拼接后的输出通道数为24+16+24+24=88个self.conv2 = nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10)self.incep2 = InceptionA(in_channels=20)self.mp = nn.MaxPool2d(2)#关于1408：#每次卷积核是5x5，则卷积后原28x28的图像变为24x24的#再经过最大池化，变为12x12的#以此类推最终得到4x4的图像，又inception输出通道88，则转为一维后为88x4x4=1408个self.fc = nn.Linear(1408, 10)def forward(self,x):in_size = x.size(0)x = F.relu(self.mp(self.conv1(x)))x = self.incep1(x)x = F.relu(self.mp(self.conv2(x)))x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return x

总结

GooLeNet在于强调去把网络做得更加深层，借此使网络变得更为复杂。

ResNet (残差网络)

问题引入

若将某个大小固定的卷积核进行反复迭代，会不会得到更好的结果。

但事实上，以CIFAR-10为例，对于$3\times 3$的卷积而言，20层的训练效果要优于56层。由图中可以明显看出，在训练集以及测试集中，20层的误差是更小的。

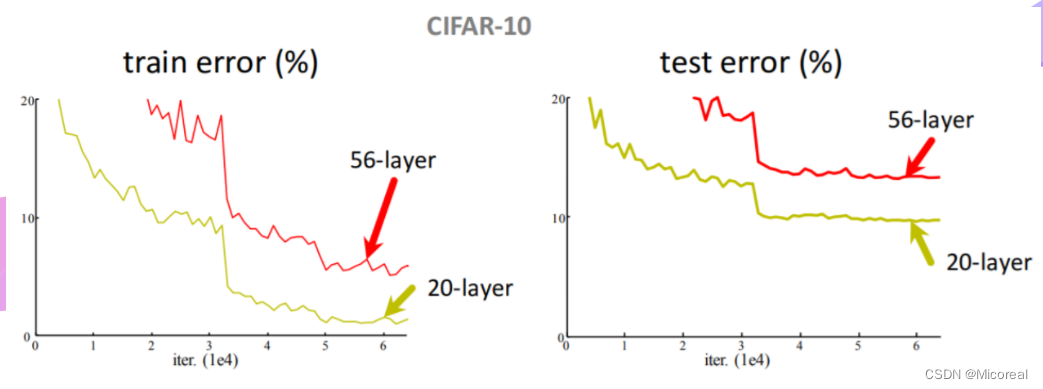
其中最可能的原因是梯度消失问题。

梯度消失

由于在梯度计算的过程中是用的反向传播，所以需要利用链式法则来进行梯度计算，是一个累乘的过程。若每一个地方梯度都是小于1的，即
$$\frac{\partial cost}{\partial \omega }<1$$
,则累乘之后的总结果应趋近于0，即
$$\frac{\partial Cost}{\partial \Omega }\to 0$$
由原先权重更新公式
$$\omega =\omega -\alpha \frac{\partial cost}{\partial \omega }$$
可知，$\frac{\partial cost}{\partial \omega }$趋近于0，则$\omega$不会再进行进一步的更新。由于深度学习的网络层数较多，为了解决梯度消失问题，从而产生了ResNet。

与传统神经网络的比较

在Residual Net中引入了跳链接，即让输入在N（一般$N=2$）层连接后并入第N层的输出，实现如图所示的
$$H(x)=F(x)+x$$
之后再进行relu激活,以此来得到输出。

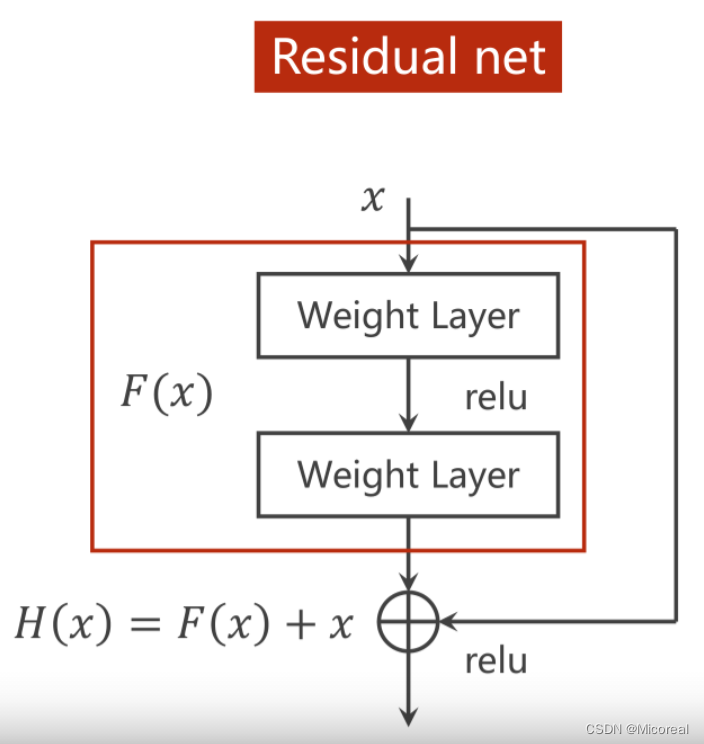
在这样的结构中，以上图为例，如果要进行$H(x)$对$x$的求导，则会有
$$\frac{\partial H(x)}{\partial x}=\frac{\partial F(x)}{\partial x}+1$$
即，若存在梯度消失现象，即存在某一层网络中的$\frac{\partial F(x)}{\partial x}\to 0$,由于上式存在，则会使得在方向传播过程中，传播的梯度会保持在1左右，即$\frac{\partial H(x)}{\partial x}\to 1$.如此，离输入较近的层也可以得到充分的训练。

代码实现

由于在ResNet中，跳链接需要实现一个权重层结果与输入相加的操作，则需要保证权重层的输出结果，与输入的维度是相同的。即等宽等高等通道数。

上图中标问号的红色块是残差块，其输入以及输出层的大小应当保持一致。

class RsidualBlock(nn.Module):def __init__(self, in_channels):super(RsidualBlock, self).__init__()#保持输出和输入一致self.channels = in_channelsself.conv1 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(in_channels, in_channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))#第二层先求和再激活y = self.conv2(y)return F.relu(x+y)

结构代码：

class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 16, kernel_size=5)self.conv2 = nn.Conv2d(16, 32, kernel_size=5)self.mp - nn.MaxPool2d(2)self.rblock1 = ResiduleBlock(in_channels=16)self.rblock2 = ResidualBlock(in_channels=32)self.fc = nn.Linear(512, 10)def forward(self,x):in_size = x.size(0)x = self.mp(F.relu(self.conv1(x)))x = self.rblock1(x)x = self.mp(F.relu(self.conv2(x)))x = self.rblock2(x)x = x.view(in_size, -1)x = self.fc(x)return x