LeetCode初级算法题:两数之和+斐波拉契数列多种java解法
目录
- 7 两数之和
- 题目描述:
- 解题思路与代码
- 暴力解法:
- 解法一:二分查找
- 解法二:双指针
- 2 斐波那契数列
- 题目描述:
- 解题思路与代码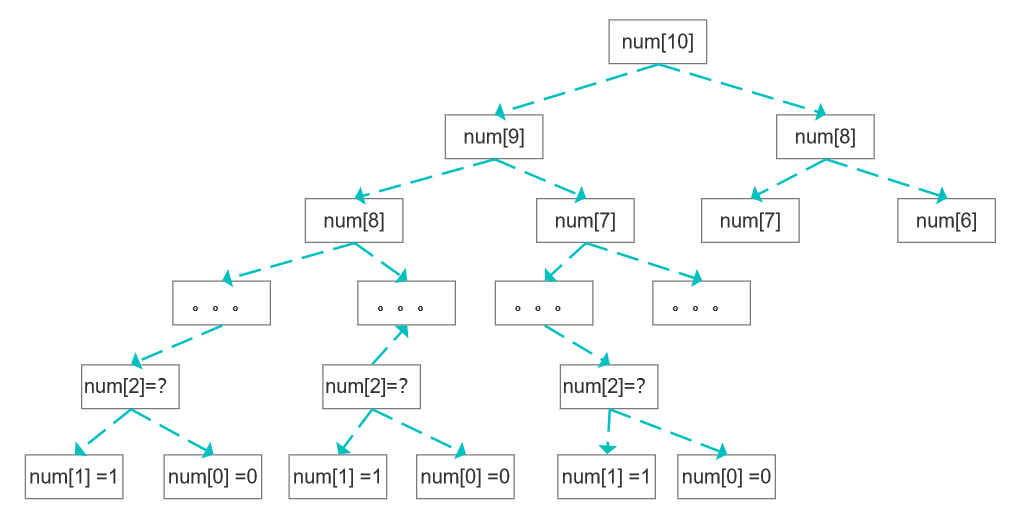
- 解法一:暴力递归
- 解法二:去重递归
- 解法三:双指针迭代
7 两数之和
题目描述:
给定一个升序排列的整数数组 numbers ,从数组中找出两个数满足相加之和等于目标数 target 。
假设每个输入只对应唯一的答案,而且不可以重复使用相同的元素。
返回两数的下标值,以数组形式返回
解题思路与代码
暴力解法:
public int[] twoSum(int[] nums, int target) {int n = nums.length;for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {if (nums[i] + nums[j] == target) {return new int[]{i, j};}}}return new int[0];}
时间复杂度:O(N的平方)
空间复杂度:O(1)
哈希表:将数组的值作为key存入map,target - num作为key
public int[] twoSum(int[] nums, int target) {Map<Integer, Integer> map = new HashMap<Integer, Integer>();for (int i = 0; i < nums.length; ++i) {if (map.containsKey(target - nums[i])) {return new int[]{map.get(target - nums[i]), i};}map.put(nums[i], i);}return new int[0];}
时间复杂度:O(N)
空间复杂度:O(N)
解法一:二分查找
先固定一个值(从下标0开始),再用二分查找查另外一个值,找不到则固定值向右移动,继续二分查找
public int[] twoSearch(int[] numbers, int target) {for (int i = 0; i < numbers.length; ++i) {int low = i, high = numbers.length - 1;while (low <= high) {int mid = (high - low) / 2 + low;if (numbers[mid] == target - numbers[i]) {return new int[]{i, mid};} else if (numbers[mid] > target - numbers[i]) {high = mid - 1;} else {low = mid + 1;}}}}
时间复杂度:O(N * logN)
空间复杂度:O(1)
解法二:双指针
左指针指向数组head,右指针指向数组tail,head+tail > target 则tail 左移,否则head右移
public int[] twoPoint(int[] numbers, int target) {int low = 0, high = numbers.length - 1;while (low < high) {int sum = numbers[low] + numbers[high];if (sum == target) {return new int[]{low + 1, high + 1};} else if (sum < target) {++low;} else {--high;}}return new int[]{-1, -1};}
时间复杂度:O(N)
空间复杂度:O(1)
2 斐波那契数列
题目描述:
求取斐波那契数列第N位的值。
斐波那契数列:每一位的值等于他前两位数字之和。前两位固定
解题思路与代码
解法一:暴力递归
public static int calculate(int num){if(num == 0 ){return 0;}if(num == 1){return 1;}return calculate(num-1) + calculate(num-2);}
解法二:去重递归
递归得出具体数值之后、存储到一个集合(下标与数列下标一致),后面递归之前先到该集合查询一次,如果查到则无需递归、直接取值。查不到再进行递归计算
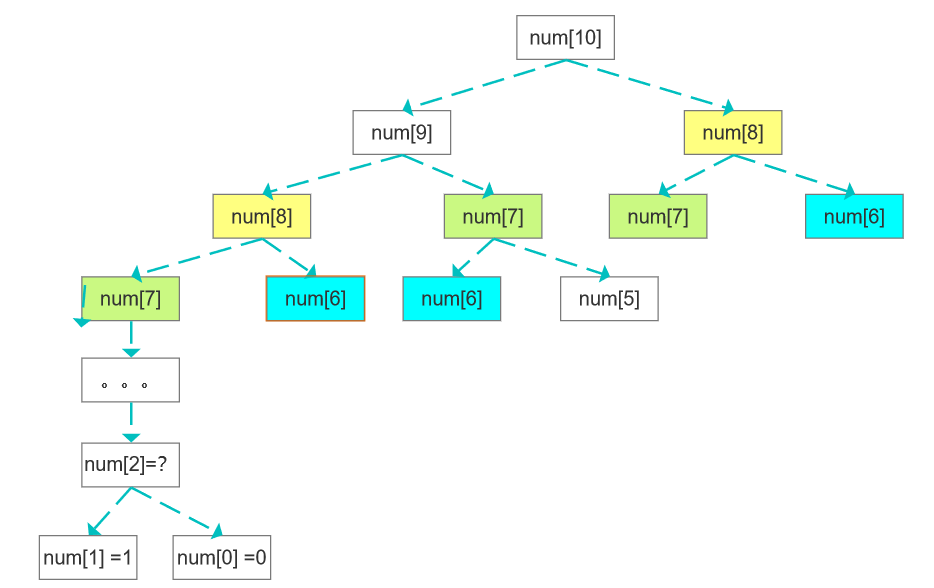
public static int calculate2(int num){int[] arr = new int[num+1];return recurse(arr,num);}private static int recurse(int[] arr, int num) {if(num == 0 ){return 0;}if(num == 1){return 1;}if(arr[num] != 0){return arr[num];}arr[num] = recurse(arr,num-1) + recurse(arr,num-2);return arr[num];}解法三:双指针迭代
基于去重递归优化,集合没有必要保存每一个下标值,只需保存前两位即可,向后遍历,得出N的值

public static int iterate(int num){if(num == 0 ){return 0;}if(num == 1){return 1;}int low = 0,high = 1;for(int i=2; i<= num; i++){int sum = low + high;low = high;high = sum;}return high;}
