LeetCode·每日一题·1223.掷骰子模拟·记忆化搜索
作者:小迅
链接:https://leetcode.cn/problems/dice-roll-simulation/solutions/2103471/ji-yi-hua-sou-suo-zhu-shi-chao-ji-xiang-xlfcs/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
题目

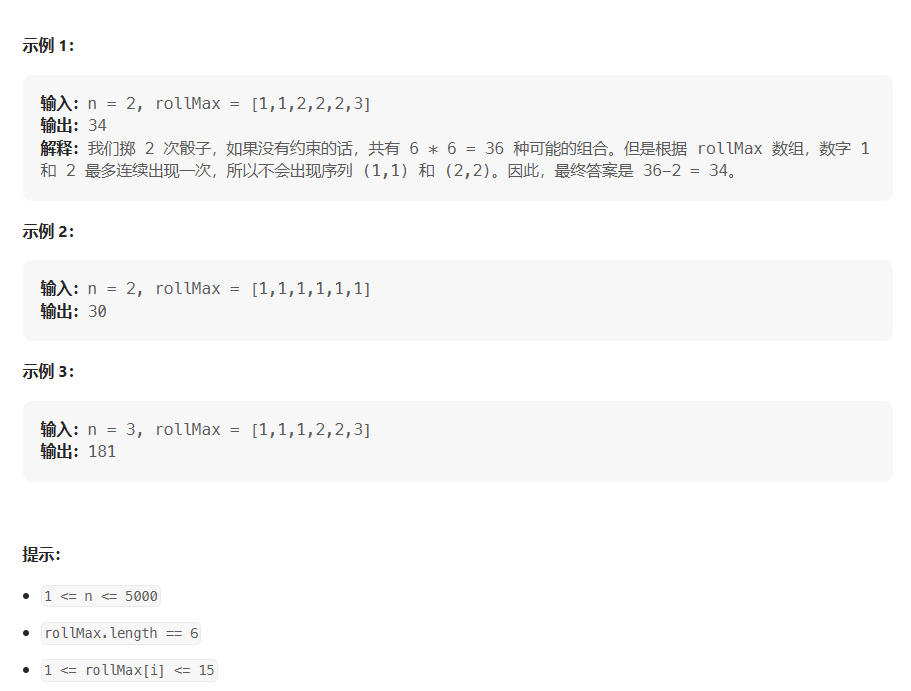
示例
思路
题意 -> 给定一个字符串规定相同类型的骰子连续出现的最大值,返回投掷 n 次后能出现的 骰数 的不同序列个数
题目说是 骰子模拟,那么直接按照题目意思进行模拟呢?
想一想,掷了一个骰子(设值为 x)后,会发生什么情况?
既然题目有 rollMax 的限制,那么分类讨论:
如果和上一个骰子值相同,那么 x 的连续出现次数不能超过 rollMax[x];
如果不同,那么可以重置连续出现次数为 1。
关键词提取:「上一个骰子值」 和 「连续出现次数」
那么在回溯中就需要知道(为了方便后面转成递推,定义成剩余):
剩余掷骰子的次数,用 i 表示;
上一个骰子值,用 last 表示;
last 的剩余连续出现次数,用 left 表示。
这样就确定了递归的参数,递归的返回值就是骰子序列个数。
要递归到哪里去呢?我们可以用回溯中的经典技巧「枚举选哪个」:
如果选的骰子值和上一个相同,且 left>0,那么递归到 (i−1,last,left−1);
如果不同,设为 j,那么递归到 (i−1,j,rollMax[j]−1)。
枚举 j=0,1,2,3,4,5,把递归后的结果相加,就是当前 (i,last,left) 的答案。
递归到 n=0 时结束,返回 1,表示找到了一个合法骰子序列
整个回溯过程是有大量重复递归调用的。由于递归函数没有副作用,无论多少次调用 dfs(i,last,left) 算出来的结果都是一样的,因此可以用记忆化搜索来优化:
如果一个状态(递归入参)是第一次遇到,那么可以在返回前,把状态及其结果记到一个 cache 数组(或者哈希表)中;
如果一个状态不是第一次遇到,那么直接返回 cache 中保存的结果。
cache[n][x][y] - n 表示 当前剩余投掷次数, x 表示上一次投掷骰子值, y表示 上一次投掷骰子值 剩余的出现次数;
为啥可以到达记忆化效果,因为当前投掷结果的有效性只和上一次的投掷结果相关,「先掷 1 后掷 3」和「先掷 2 后掷 3」,都会递归到 dfs(n−2,3,rollMax[3]−1)。
如何转动态规划 :
可以去掉递归中的「递」,只保留「归」的部分,即自底向上计算。
做法:
dfs 改成 f 数组;
递归改成循环(每个参数都对应一层循环);
递归边界改成 f 数组的初始值。
代码注释超级详细
代码
const long MOD = 1e9 + 7;int dfs(int i, int last, int *rollMax, int left, int (*cache)[6][15])
{if (i == 0) return 1;int *c = (int *)&(cache[i][last][left]);if (*c >= 0) return *c;//如果之前算过就不需要重新计算long res = 0;for (int j = 0; j < 6; ++j)if (j != last) res += dfs(i - 1, j, rollMax, rollMax[j] - 1, cache);else if (left) res += dfs(i - 1, j, rollMax, left - 1, cache);return *c = res % MOD;
}int dieSimulator(int n, int* rollMax, int rollMaxSize){int cache[n][6][15];//记忆化数组memset(cache, -1, sizeof(cache)); // -1 表示没有访问过long ans = 0;for (int j = 0; j < 6; ++j)//枚举初始状态0-6ans += dfs(n - 1, j, rollMax, rollMax[j] - 1, cache);return ans % MOD;
}作者:小迅
链接:https://leetcode.cn/problems/dice-roll-simulation/solutions/2103471/ji-yi-hua-sou-suo-zhu-shi-chao-ji-xiang-xlfcs/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。class Solution {const long MOD = 1e9 + 7;
public:int dieSimulator(int n, vector<int> &rollMax) {int m = rollMax.size(), f[n][m][15];for (int j = 0; j < m; ++j)for (int k = 0; k < rollMax[j]; ++k)f[0][j][k] = 1;for (int i = 1; i < n; ++i)for (int last = 0; last < m; ++last)for (int left = 0; left < rollMax[last]; ++left) {long res = 0;for (int j = 0; j < m; ++j)if (j != last) res += f[i - 1][j][rollMax[j] - 1];else if (left) res += f[i - 1][j][left - 1];f[i][last][left] = res % MOD;}long ans = 0;for (int j = 0; j < m; ++j)ans += f[n - 1][j][rollMax[j] - 1];return ans % MOD;}
};
