当前位置：首页 > news >正文

使用 Go 语言实现二叉搜索树

news 2025/7/6 19:24:27

原文链接： 使用 Go 语言实现二叉搜索树

二叉树是一种常见并且非常重要的数据结构，在很多项目中都能看到二叉树的身影。

它有很多变种，比如红黑树，常被用作 std::map 和 std::set 的底层实现；B 树和 B+ 树，广泛应用于数据库系统中。

本文要介绍的二叉搜索树用的也很多，比如在开源项目 go-zero 中，就被用来做路由管理。

这篇文章也算是一篇前导文章，介绍一些必备知识，下一篇再来介绍具体在 go-zero 中的应用。

二叉搜索树的特点

最重要的就是它的有序性，在二叉搜索树中，每个节点的值都大于其左子树中的所有节点的值，并且小于其右子树中的所有节点的值。

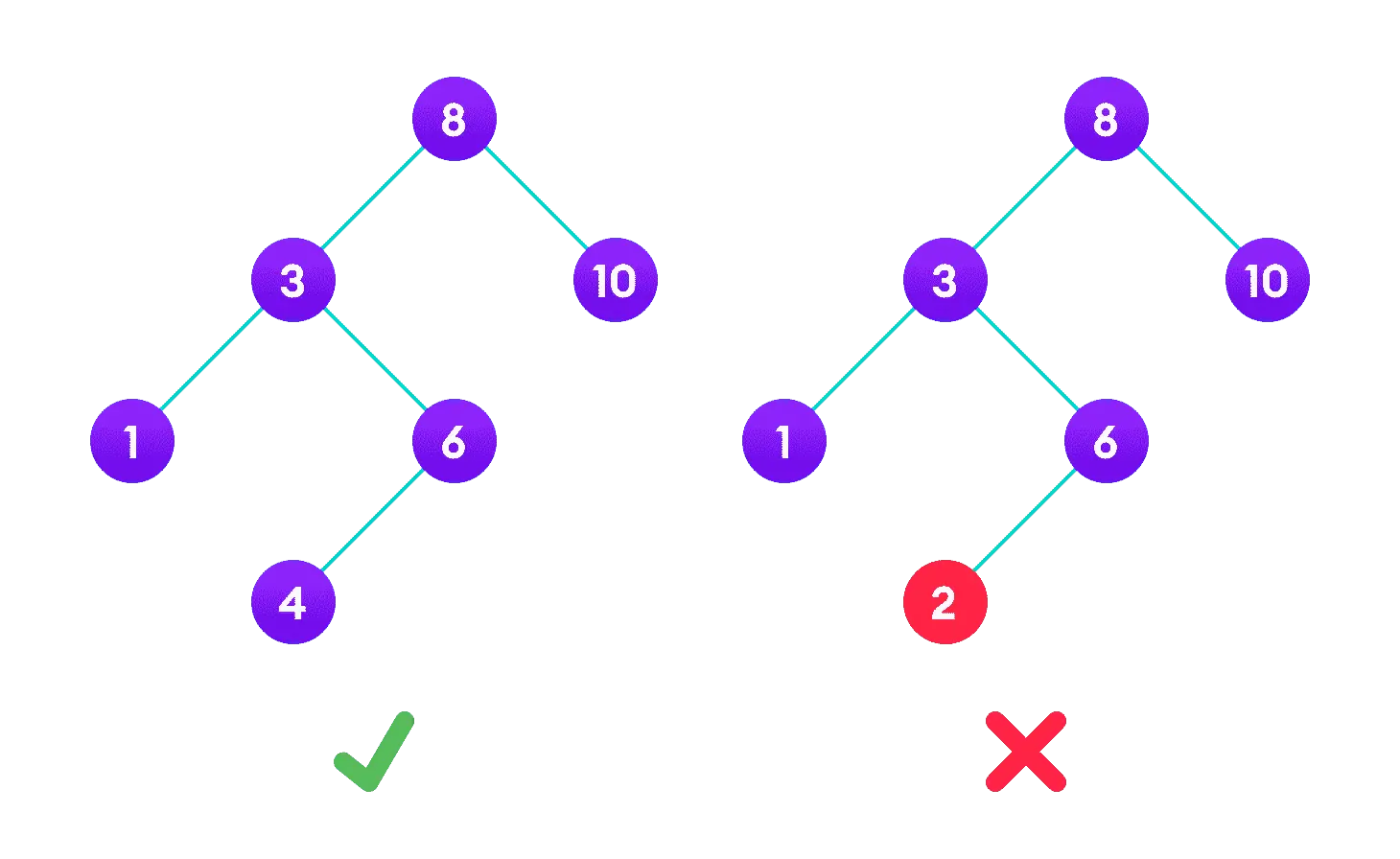
这意味着通过二叉搜索树可以快速实现对数据的查找和插入。

Go 语言实现

本文主要实现了以下几种方法：

Insert(t)：插入一个节点
Search(t)：判断节点是否在树中
InOrderTraverse()：中序遍历
PreOrderTraverse()：前序遍历
PostOrderTraverse()：后序遍历
Min()：返回最小值
Max()：返回最大值
Remove(t)：删除一个节点
String()：打印一个树形结构

下面分别来介绍，首先定义一个节点：

type Node struct {key   intvalue Itemleft  *Node //leftright *Node //right
}

定义树的结构体，其中包含了锁，是线程安全的：

type ItemBinarySearchTree struct {root *Nodelock sync.RWMutex
}

插入操作：

func (bst *ItemBinarySearchTree) Insert(key int, value Item) {bst.lock.Lock()defer bst.lock.Unlock()n := &Node{key, value, nil, nil}if bst.root == nil {bst.root = n} else {insertNode(bst.root, n)}
}// internal function to find the correct place for a node in a tree
func insertNode(node, newNode *Node) {if newNode.key < node.key {if node.left == nil {node.left = newNode} else {insertNode(node.left, newNode)}} else {if node.right == nil {node.right = newNode} else {insertNode(node.right, newNode)}}
}

在插入时，需要判断插入节点和当前节点的大小关系，保证搜索树的有序性。

中序遍历：

func (bst *ItemBinarySearchTree) InOrderTraverse(f func(Item)) {bst.lock.RLock()defer bst.lock.RUnlock()inOrderTraverse(bst.root, f)
}// internal recursive function to traverse in order
func inOrderTraverse(n *Node, f func(Item)) {if n != nil {inOrderTraverse(n.left, f)f(n.value)inOrderTraverse(n.right, f)}
}

前序遍历：

func (bst *ItemBinarySearchTree) PreOrderTraverse(f func(Item)) {bst.lock.Lock()defer bst.lock.Unlock()preOrderTraverse(bst.root, f)
}// internal recursive function to traverse pre order
func preOrderTraverse(n *Node, f func(Item)) {if n != nil {f(n.value)preOrderTraverse(n.left, f)preOrderTraverse(n.right, f)}
}

后序遍历：

func (bst *ItemBinarySearchTree) PostOrderTraverse(f func(Item)) {bst.lock.Lock()defer bst.lock.Unlock()postOrderTraverse(bst.root, f)
}// internal recursive function to traverse post order
func postOrderTraverse(n *Node, f func(Item)) {if n != nil {postOrderTraverse(n.left, f)postOrderTraverse(n.right, f)f(n.value)}
}

返回最小值：

func (bst *ItemBinarySearchTree) Min() *Item {bst.lock.RLock()defer bst.lock.RUnlock()n := bst.rootif n == nil {return nil}for {if n.left == nil {return &n.value}n = n.left}
}

由于树的有序性，想要得到最小值，一直向左查找就可以了。

返回最大值：

func (bst *ItemBinarySearchTree) Max() *Item {bst.lock.RLock()defer bst.lock.RUnlock()n := bst.rootif n == nil {return nil}for {if n.right == nil {return &n.value}n = n.right}
}

查找节点是否存在：

func (bst *ItemBinarySearchTree) Search(key int) bool {bst.lock.RLock()defer bst.lock.RUnlock()return search(bst.root, key)
}// internal recursive function to search an item in the tree
func search(n *Node, key int) bool {if n == nil {return false}if key < n.key {return search(n.left, key)}if key > n.key {return search(n.right, key)}return true
}

删除节点：

func (bst *ItemBinarySearchTree) Remove(key int) {bst.lock.Lock()defer bst.lock.Unlock()remove(bst.root, key)
}// internal recursive function to remove an item
func remove(node *Node, key int) *Node {if node == nil {return nil}if key < node.key {node.left = remove(node.left, key)return node}if key > node.key {node.right = remove(node.right, key)return node}// key == node.keyif node.left == nil && node.right == nil {node = nilreturn nil}if node.left == nil {node = node.rightreturn node}if node.right == nil {node = node.leftreturn node}leftmostrightside := node.rightfor {//find smallest value on the right sideif leftmostrightside != nil && leftmostrightside.left != nil {leftmostrightside = leftmostrightside.left} else {break}}node.key, node.value = leftmostrightside.key, leftmostrightside.valuenode.right = remove(node.right, node.key)return node
}

删除操作会复杂一些，分三种情况来考虑：

如果要删除的节点没有子节点，只需要直接将父节点中，指向要删除的节点指针置为 nil 即可
如果删除的节点只有一个子节点，只需要更新父节点中，指向要删除节点的指针，让它指向删除节点的子节点即可
如果删除的节点有两个子节点，我们需要找到这个节点右子树中的最小节点，把它替换到要删除的节点上。然后再删除这个最小节点，因为最小节点肯定没有左子节点，所以可以应用第二种情况删除这个最小节点即可

最后是一个打印树形结构的方法，在实际项目中其实并没有实际作用：

func (bst *ItemBinarySearchTree) String() {bst.lock.Lock()defer bst.lock.Unlock()fmt.Println("------------------------------------------------")stringify(bst.root, 0)fmt.Println("------------------------------------------------")
}// internal recursive function to print a tree
func stringify(n *Node, level int) {if n != nil {format := ""for i := 0; i < level; i++ {format += "       "}format += "---[ "level++stringify(n.left, level)fmt.Printf(format+"%d\n", n.key)stringify(n.right, level)}
}

单元测试

下面是一段测试代码：

func fillTree(bst *ItemBinarySearchTree) {bst.Insert(8, "8")bst.Insert(4, "4")bst.Insert(10, "10")bst.Insert(2, "2")bst.Insert(6, "6")bst.Insert(1, "1")bst.Insert(3, "3")bst.Insert(5, "5")bst.Insert(7, "7")bst.Insert(9, "9")
}func TestInsert(t *testing.T) {fillTree(&bst)bst.String()bst.Insert(11, "11")bst.String()
}// isSameSlice returns true if the 2 slices are identical
func isSameSlice(a, b []string) bool {if a == nil && b == nil {return true}if a == nil || b == nil {return false}if len(a) != len(b) {return false}for i := range a {if a[i] != b[i] {return false}}return true
}func TestInOrderTraverse(t *testing.T) {var result []stringbst.InOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"1", "2", "3", "4", "5", "6", "7", "8", "9", "10", "11"}) {t.Errorf("Traversal order incorrect, got %v", result)}
}func TestPreOrderTraverse(t *testing.T) {var result []stringbst.PreOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"}) {t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"8", "4", "2", "1", "3", "6", "5", "7", "10", "9", "11"})}
}func TestPostOrderTraverse(t *testing.T) {var result []stringbst.PostOrderTraverse(func(i Item) {result = append(result, fmt.Sprintf("%s", i))})if !isSameSlice(result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"}) {t.Errorf("Traversal order incorrect, got %v instead of %v", result, []string{"1", "3", "2", "5", "7", "6", "4", "9", "11", "10", "8"})}
}func TestMin(t *testing.T) {if fmt.Sprintf("%s", *bst.Min()) != "1" {t.Errorf("min should be 1")}
}func TestMax(t *testing.T) {if fmt.Sprintf("%s", *bst.Max()) != "11" {t.Errorf("max should be 11")}
}func TestSearch(t *testing.T) {if !bst.Search(1) || !bst.Search(8) || !bst.Search(11) {t.Errorf("search not working")}
}func TestRemove(t *testing.T) {bst.Remove(1)if fmt.Sprintf("%s", *bst.Min()) != "2" {t.Errorf("min should be 2")}
}