当前位置： 首页 > news >正文

一起来学算法（邻接矩阵）

news 2025/7/18 3:23:12

前言：

       邻接矩阵是数学和计算机科学中常用的一种表示方式，用来表述有向图或无向图，一张图由一组顶点（或结点）和一组表组成，用邻接矩阵就能表示这些顶点间存在的边的关系

1.图的概念

       对于图而言，是数据结构中最复杂的结构，而是在做题的过程中，最大的难点在于BFS和DFS的过程，图从两个维度划分可以有：有向图、无权图、带权图。

1.有向图和无向图：

        在无向图中，边没有方向，表示的是双向关系，换句话来说，如果两个顶点（或结点）之间存在边，那么这两个顶点就互相连接

 

        例如，如果你正在建模一个社交网络，你可能会使用无向图，因为友谊是双向，如果1是2的朋友，那么2也是1的朋友，如图示：

       有向图：与无向图相反，有向图的边有方向，表示单向关系，在这种图中，如果存在从1到2的边，那不一定存在从2到1的边，如图所示：

 2.无权图和带权图

在图论中，图可以是无权的也可以是带权的，这主要取决于边是否具有与其关联的值（权重）

无权图：

       在无权图中，边没有权重，或者说所有边的权重都是相同的，你只关心两个节点（顶点）之间是否存在边，而不是关心边的长度或者是成本，比如，社交网络的人际关心就可以用无权图来表示，如果两个人是朋友，就有一条边连接它们，所有的边都被视为相等

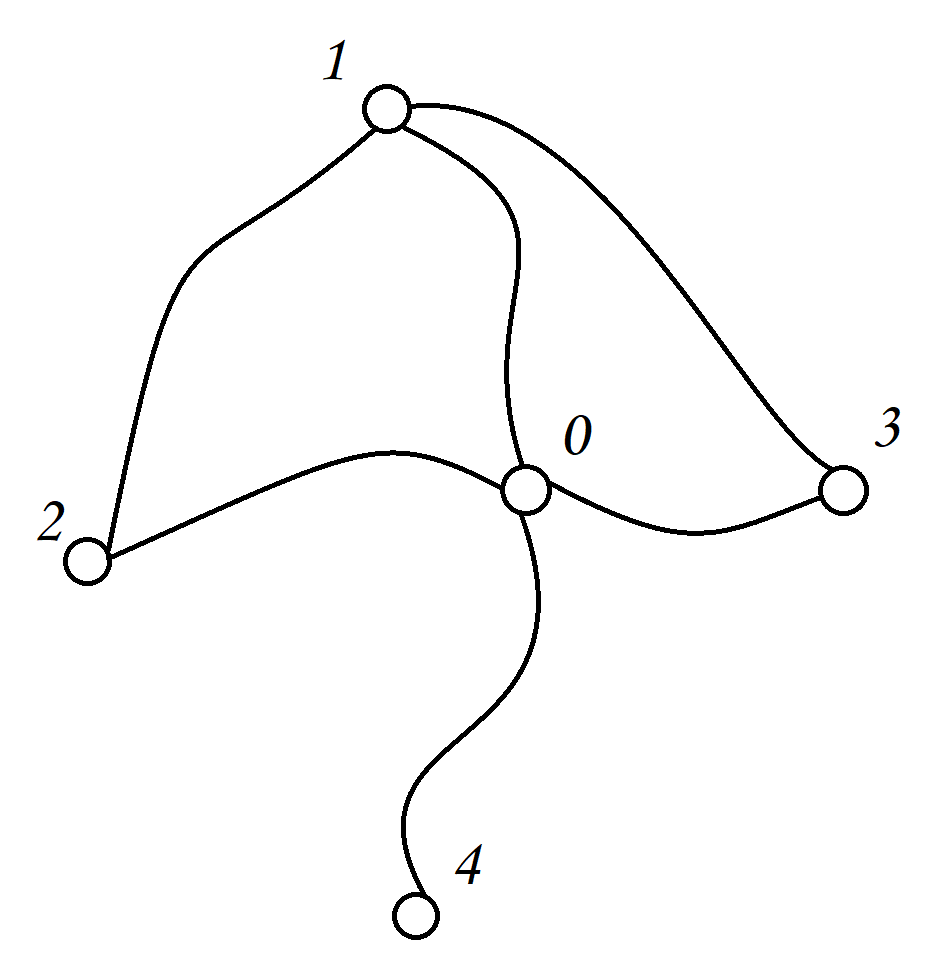
 带权图：

       与无权图相对，带权图中的边有各自的权重，这个权重可以表示很多的意义，如距离、时间、成本等等，取决于你要了解的问题，比如，在导航应用中，每个结点可以代表一个结点，边的权重就可以代表两个地点之间的距离或者是行驶时间，在这种情况下，你不仅关心结点之间是否存在边，还关心这个边的权重是多少

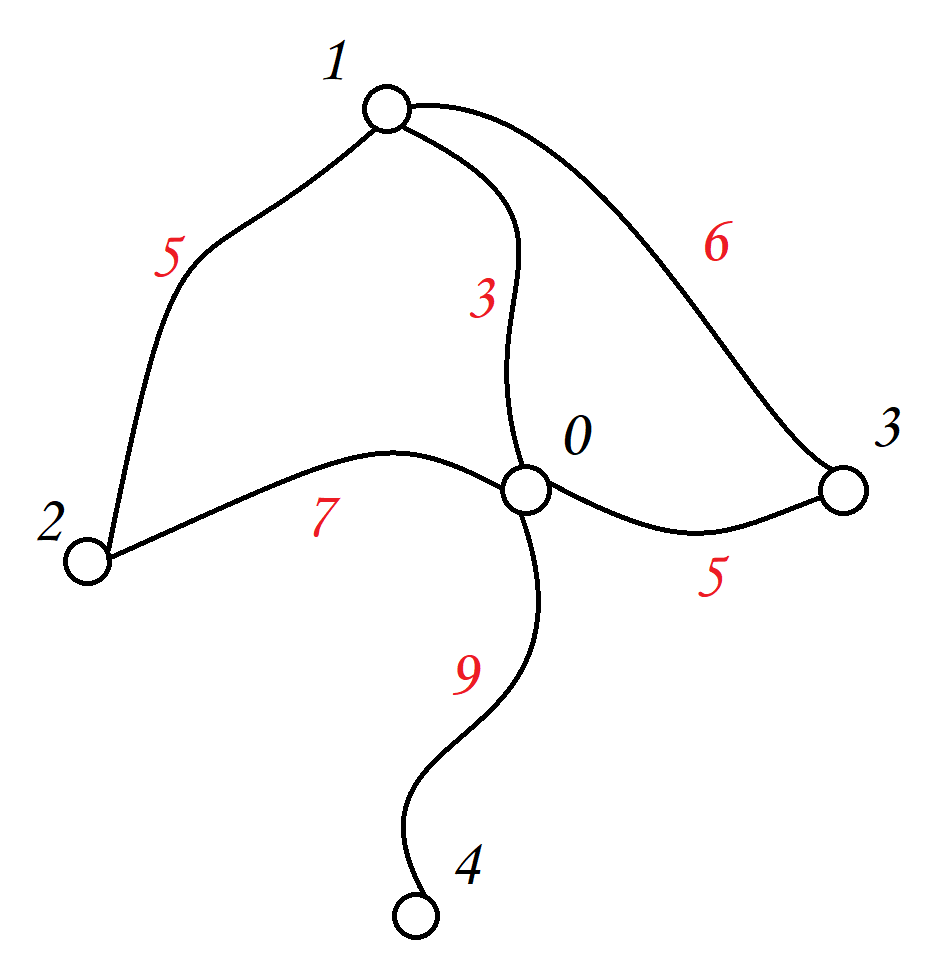
 2.邻接矩阵的概念

        注意：对于邻接矩阵而言 ，不需要去考虑是有向的还是无向的，统一都可以理解成有向的，因为有向图可以兼容无向图，对于无向图而言，只不过这个矩阵按照主对角线对称，因为A到B有变，则必然B到A有边

1.无权图的邻接矩阵

在这样一个矩阵里：

1.矩阵中的行和列都是对应图中的一个顶点

2.如果顶点A到顶点B有一条边（这里是单向的），则对应矩阵单元为1

3.如果顶点A到顶点B没有边，则对应的矩阵单元就为0

如下图所示：

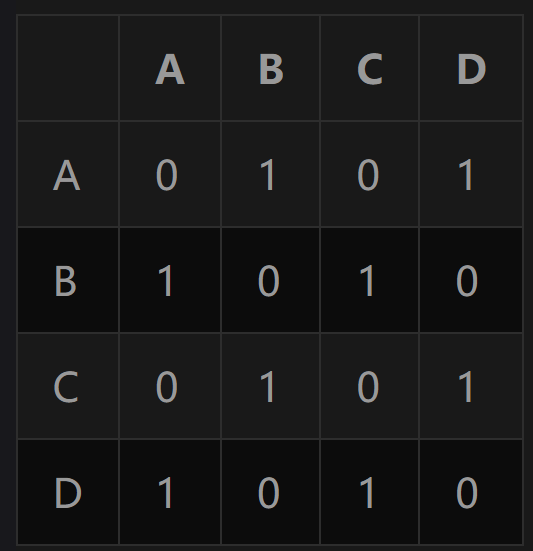
       从这个矩阵中我们可以看出，A节点能够到达B、D节点，B节点能够到达A、C节点，C节点能够到达B、D节点，D节点能够到达A、C节点，所以如图所示：

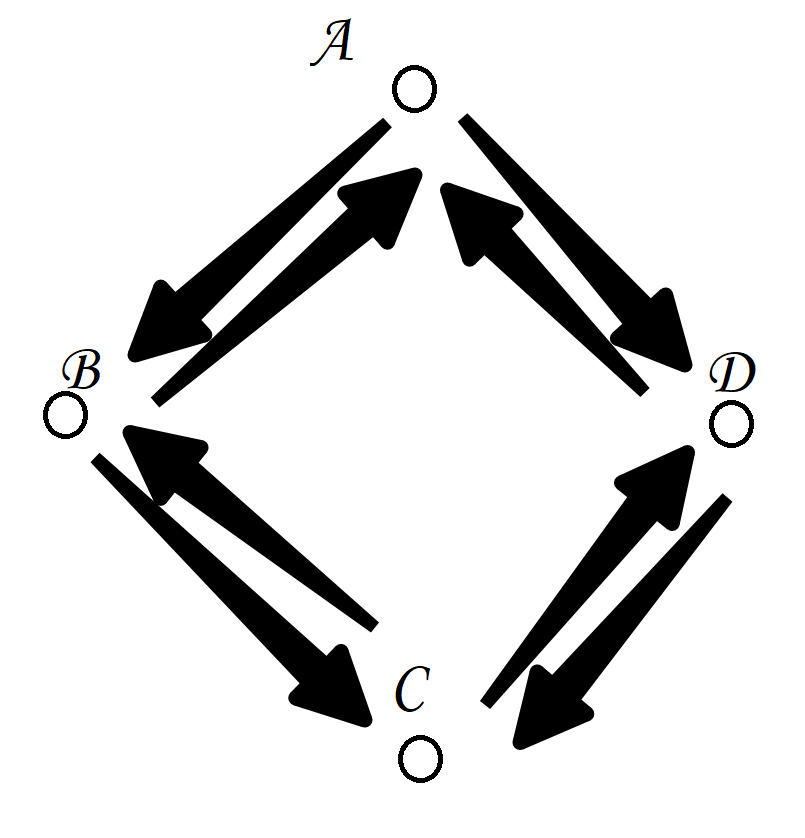
 2.带权图的邻接矩阵

        在带权图的邻接矩阵中，每个矩阵元素表示一个有向边的权值，如果不存在从一个结点到另一个节点的边，则通常将其表示为特殊的值（0、-1均可）

  • A->B   权重为3
  • A->C   权重为7
  • B->A   权重为4
  • B->D   权重为1
  • C->D   权重为2
  • D->A   权重为1

该邻接矩阵为：

 3.邻接矩阵的代码实现

/*** 图的表示--使用邻接矩阵*/
public class Graph01 {private char[] V;//顶点上的值private Vertex[] vertexs;//顶点数组private int N;//邻接矩阵private int[][] adj;//图的构造函数public Graph01(char[] arr) {//{'A','E','F','G','H','P'}//拿到数组的长度int length = arr.length;this.N = length;V = new char[length];//arr元素赋值 到Vthis.V = Arrays.copyOf(arr, length);//构建图中的结点vertexs = new Vertex[length];for (int i = 0; i < length; i++) {vertexs[i] = new Vertex(i,this.V[i]);//}this.adj = new int[length][length];}//打印邻接矩阵public void show() {System.out.print("    ");for (int i = 0; i < this.N; i++) {System.out.format("%4c", this.V[i]);}System.out.println();for (int i = 0; i < this.N; i++) {System.out.format("%4c",this.V[i]);for (int j = 0; j < this.N; j++) {System.out.format("%4s", this.adj[i][j] > 0?(this.adj[i][j]):"-");}System.out.println();}}/*** 创建顶点类*/private class Vertex {char v;//值int index;//索引public Vertex(int index, char c) {this.index = index;this.v = v;}}public static void main(String[] args) {char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};//构建graph01Graph01 graph01 = new Graph01(arr);//进行连接int[][] adjMatrix = graph01.adj;adjMatrix[0][1]=1;adjMatrix[0][2]=1;adjMatrix[0][3]=1;adjMatrix[1][0]=1;adjMatrix[1][3]=1;adjMatrix[1][4]=1;adjMatrix[2][0]=1;adjMatrix[3][0]=1;adjMatrix[3][1]=1;adjMatrix[3][4]=1;adjMatrix[3][5]=1;adjMatrix[4][1]=1;adjMatrix[4][3]=1;adjMatrix[4][5]=1;adjMatrix[5][3]=1;adjMatrix[5][4]=1;graph01.show();}
*** 图的表示--使用邻接矩阵*/
public class Graph02 {private char[] V;//顶点上的值private Vertex[] vertexs;//顶点数组private int N;//邻接矩阵private List<Integer>[] adj;//图的构造函数public Graph02(char[] arr) {//{'A','E','F','G','H','P'}//拿到数组的长度int length = arr.length;this.N = length;V = new char[length];//arr元素赋值 到Vthis.V = Arrays.copyOf(arr, length);//构建图中的结点vertexs = new Vertex[length];for (int i = 0; i < length; i++) {vertexs[i] = new Vertex(i, this.V[i]);}this.adj = new List[length];for (int i = 0; i < this.N; i++) {this.adj[i]=new ArrayList<>();}}//打印邻接矩阵public void show() {System.out.println("    ");for (int i = 0; i < this.N; i++) {System.out.format("%-4c", this.V[i]);//拿到邻接表相邻结点的集合List<Integer> linkedList = this.adj[i];for (int j = 0; j < linkedList.size(); j++) {System.out.print(this.V[linkedList.get(j)] + "---->");}System.out.println();System.out.format("%-4d",vertexs[i].index);for (int j = 0; j < linkedList.size(); j++) {System.out.print(vertexs[linkedList.get(j)].index + "---->");}System.out.println();}}/*** 创建顶点类*/private class Vertex {char v;//值int index;//索引int weight;//权值public Vertex(int index, char c) {this.index = index;this.v = v;this.weight = weight;}public Vertex(int index) {}}public static void main(String[] args) {char arr[] = {'A', 'E', 'F', 'G', 'H', 'P'};//构建graph01Graph02 graph02 = new Graph02(arr);//邻接表List<Integer>[] adj = graph02.adj;adj[0].add(1);adj[0].add(2);adj[0].add(3);adj[1].add(0);adj[1].add(3);adj[1].add(4);adj[2].add(0);adj[3].add(0);adj[3].add(1);adj[3].add(4);adj[3].add(5);adj[4].add(1);adj[4].add(3);adj[4].add(5);adj[5].add(3);adj[5].add(4);graph02.show();}

leetcode题单：

省份数量

//进行广度优先搜索public int findCircleNum(int[][] isConnected) {if(isConnected==null||isConnected.length==0){return 0;}int privice=0;Queue<Integer> queue=new LinkedList<>();boolean[] visited=new boolean[isConnected.length];Arrays.fill(visited,false);//对每一个城市进行遍历，得到每一个城市与相连的城市表for (int i = 0; i <isConnected.length; i++) {//如果是没有遍历过的城市，则进行如下操作if(!visited[i]){queue.offer(i);while(!queue.isEmpty()){int index=queue.poll();visited[index]=true;for (int j = 0; j <isConnected.length; j++) {if(isConnected[index][j]==1&&!visited[j]){queue.offer(j);}}}privice++;} }return privice;}

矩阵中的最长递增路径

LCP07.传递信息

http://www.lryc.cn/news/105007.html

相关文章：

  • hadoop与HDFS交互
  • MYSQL 分区如何指定不同存储路径（多块磁盘）
  • 安全加固服务器
  • Linux 命令学习：
  • 牛客网Verilog刷题——VL54
  • 学习系统编程No.34【线程同步之信号量】
  • SolidUI社区-Snakemq 通信源码分析
  • 【大数据之Flume】四、Flume进阶之复制和多路复用、负载均衡和故障转移、聚合案例
  • 前端学习--vue2--插槽
  • 使用 Docker Compose 部署 Redis Cluster 集群，轻松搭建高可用分布式缓存
  • 在Spring Boot框架中集成 Spring Security
  • 登月再进一步：Apollo自动驾驶的里程碑
  • 嵌入式一开始该怎么学？学习单片机
  • Spring事件监听器ApplicationListener
  • 安全学习DAY10_HTTP数据包
  • 云原生落地实践的25个步骤
  • Stable diffusion 三大基础脚本 提示词矩阵，载入提示词，XYZ图表讲解
  • uniapp uni-combox 下拉提示无匹配项（完美解决--附加源码解决方案及思路）
  • 10. Mybatis 项目的创建
  • 历年 Nobel prize in Physics （诺贝尔物理学奖）简介
  • IDEA中Git面板操作介绍 变基、合并、提取、拉取、签出
  • Android Studio开发简易APP添加代办事项
  • python 统计所有的 仓库 提交者的提交次数
  • 018-从零搭建微服务-系统服务（五）
  • HarmonyOS 开发基础（三）登录页面单向数据绑定（父组件向子组件传参）
  • 发npm包
  • ＜el-empty＞
  • IO流（4）- 序列化流与反序列化流
  • 人工智能如何应对 DevOps 监控和可观测性挑战
  • 数字化新时代，VR全景拍摄与制作