多激光雷达手眼标定
手眼标定方法已经有很多博客进行解析,但是都是针对机器人的手(夹爪)眼睛(相机)进行标定。例如:
标定学习笔记(四)-- 手眼标定详解
手眼标定_全面细致的推导过程
本文主要描述多激光雷达应用中如何使用手眼标定的方法进行标定。
假如存在以下问题,在一个小车上存在两个激光雷达,激光雷达A与激光雷达B,须求解激光雷达B到激光雷达A的转换参数 B A T ^A_BT BAT(外参)。
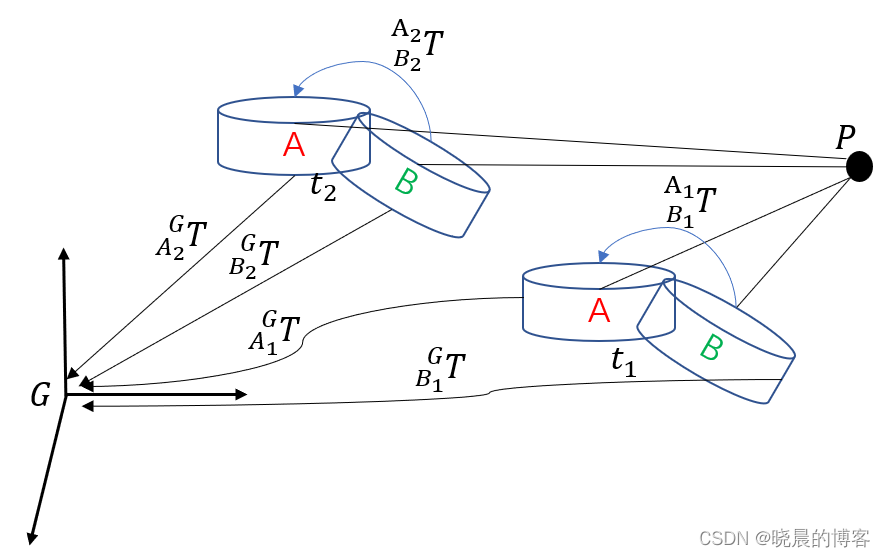
利用手眼标定方法原理如下:
变量定义
如上图中所示,存在一个世界坐标系G,点 P P P在世界坐标系中的坐标为 P G P_G PG。
在 t 1 t_1 t1时刻,激光雷达A与激光雷达B分别观测到点 P P P的坐标为: P A 1 P_{A1} PA1, P B 1 P_{B1} PB1。
在 t 2 t_2 t2时刻,激光雷达A与激光雷达B分别观测到点 P P P的坐标为: P A 2 P_{A2} PA2, P B 2 P_{B2} PB2。
在 t 1 t_1 t1时刻,激光雷达A与激光雷达B分别到全局坐标系 G G G的转换关系为: A 1 G T ^{G}_{A1}T A1GT, B 1 G T ^{G}_{B1}T B1GT。
在 t 2 t_2 t2时刻,激光雷达A与激光雷达B分别到全局坐标系 G G G的转换关系为: A 2 G T ^{G}_{A2}T A2GT, B 2 G T ^{G}_{B2}T B2GT。
在 t 1 t_1 t1时刻,激光雷达A与激光雷达B之间的转换关系为 B 1 A 1 T ^{A1}_{B1}T B1A1T
在 t 2 t_2 t2时刻,激光雷达A与激光雷达B之间的转换关系为 B 2 A 2 T ^{A2}_{B2}T B2A2T
推导过程
在 t 1 t_1 t1时刻,点 P P P在世界坐标系中的坐标 P G P_G PG可以通过下式计算:
P G = ( A 1 G T ) ( B 1 A 1 T ) P B 1 P_G=(^{G}_{A1}T)(^{A1}_{B1}T)P_{B1} PG=(A1GT)(B1A1T)PB1
在 t 2 t_2 t2时刻,
P G = ( A 2 G T ) ( B 2 A 2 T ) P B 2 P_G=(^{G}_{A2}T)(^{A2}_{B2}T)P_{B2} PG=(A2GT)(B2A2T)PB2
由上述两式可得:
P G = ( A 1 G T ) ( B 1 A 1 T ) P B 1 = ( A 2 G T ) ( B 2 A 2 T ) P B 2 = P G P_G=(^{G}_{A1}T)(^{A1}_{B1}T)P_{B1}=(^{G}_{A2}T)(^{A2}_{B2}T)P_{B2}=P_G PG=(A1GT)(B1A1T)PB1=(A2GT)(B2A2T)PB2=PG
由于认为激光雷达A与激光雷达B之间是刚性连接,所以二者之间的变换不随时间进行变化,即:
B 1 A 1 T = B 2 A 2 T = B A T ^{A1}_{B1}T=^{A2}_{B2}T=^{A}_{B}T B1A1T=B2A2T=BAT
则上式变换为:
( A 1 G T ) ( B A T ) P B 1 = ( A 2 G T ) ( B A T ) P B 2 (^{G}_{A1}T)(^{A}_{B}T)P_{B1}=(^{G}_{A2}T)(^{A}_{B}T)P_{B2} (A1GT)(BAT)PB1=(A2GT)(BAT)PB2
两边同左乘 ( A 2 G T ) − 1 (^{G}_{A2}T)^{-1} (A2GT)−1,并同时右乘 ( P B 1 ) − 1 (P_{B1})^{-1} (PB1)−1,转换为下式:
( A 2 G T ) − 1 ( A 1 G T ) ( B A T ) = ( B A T ) P B 2 ( P B 1 ) − 1 (^{G}_{A2}T)^{-1}(^{G}_{A1}T)(^{A}_{B}T)=(^{A}_{B}T)P_{B2}(P_{B1})^{-1} (A2GT)−1(A1GT)(BAT)=(BAT)PB2(PB1)−1
假设 ( B A T ) (^{A}_{B}T) (BAT)为要求解的变量 X X X,系数为 A = ( A 2 G T ) − 1 ( A 1 G T ) A=(^{G}_{A2}T)^{-1}(^{G}_{A1}T) A=(A2GT)−1(A1GT)与 B = P B 2 ( P B 1 ) − 1 B=P_{B2}(P_{B1})^{-1} B=PB2(PB1)−1。
则上式转换为:
A X = X B AX=XB AX=XB
这就是我们经常所说的手眼标定推导出的形式了。但是,这和我们的激光雷达轨迹有什么关系呢?
接着,对系数 A A A与 B B B分别进行转换,过程如下:
对式 A A A,代入 A 1 G T = ( A 2 G T ) ( A 1 A 2 T ) ^{G}_{A1}T=(^{G}_{A2}T)(^{A2}_{A1}T) A1GT=(A2GT)(A1A2T)得:
A = ( A 2 G T ) − 1 ( A 1 G T ) = ( A 2 G T ) − 1 ( A 2 G T ) ( A 1 A 2 T ) = A 1 A 2 T A=(^{G}_{A2}T)^{-1}(^{G}_{A1}T)=(^{G}_{A2}T)^{-1}(^{G}_{A2}T)(^{A2}_{A1}T)=^{A2}_{A1}T A=(A2GT)−1(A1GT)=(A2GT)−1(A2GT)(A1A2T)=A1A2T
对式 B B B,分别代入 P B 1 = ( G B 1 T ) P G P_{B1}=(^{B1}_{G}T)P_{G} PB1=(GB1T)PG与 P B 2 = ( G B 2 T ) P G P_{B2}=(^{B2}_{G}T)P_{G} PB2=(GB2T)PG得:
B = P B 2 ( P B 1 ) − 1 = ( G B 2 T ) P G ( G B 1 T P G ) − 1 B=P_{B2}(P_{B1})^{-1}=(^{B2}_{G}T)P_{G}(^{B1}_{G}TP_{G})^{-1} B=PB2(PB1)−1=(GB2T)PG(GB1TPG)−1
= ( G B 2 T ) P G P G − 1 ( G B 1 T ) − 1 = ( G B 2 T ) ( G B 1 T ) − 1 =(^{B2}_{G}T)P_{G}P_{G}^{-1}(^{B1}_{G}T)^{-1}=(^{B2}_{G}T)(^{B1}_{G}T)^{-1} =(GB2T)PGPG−1(GB1T)−1=(GB2T)(GB1T)−1
代入 G B 2 T = ( B 1 B 2 T ) ( G B 1 T ) ^{B2}_{G}T=(^{B2}_{B1}T)(^{B1}_{G}T) GB2T=(B1B2T)(GB1T)得:
B = ( G B 2 T ) ( G B 1 T ) − 1 = ( B 1 B 2 T ) ( G B 1 T ) ( G B 1 T ) − 1 = B 1 B 2 T B=(^{B2}_{G}T)(^{B1}_{G}T)^{-1}=(^{B2}_{B1}T)(^{B1}_{G}T)(^{B1}_{G}T)^{-1}=^{B2}_{B1}T B=(GB2T)(GB1T)−1=(B1B2T)(GB1T)(GB1T)−1=B1B2T
由此,可得 A X = X B AX=XB AX=XB可以转换为下述形式:
( A 1 A 2 T ) X = X ( B 1 B 2 T ) (^{A2}_{A1}T)X=X(^{B2}_{B1}T) (A1A2T)X=X(B1B2T)
式中, A 1 A 2 T ^{A2}_{A1}T A1A2T为激光雷达 A A A从 t 1 t_1 t1时刻到 t 2 t_2 t2时刻的位姿变换(也就是轨迹)。同样的, B 1 B 2 T ^{B2}_{B1}T B1B2T为激光雷达 B B B从 t 1 t_1 t1时刻到 t 2 t_2 t2时刻的位姿变换。
