图的最短路径
最短路径算法对图结构没有特殊要求,不要求连通图,且有向图无向图均可。
最短路径算法目标是求得从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径。解决最短路的问题有以下算法:Dijkstra算法,Floyd算法和SPFA算法等。其中SPFA算法可以处理边权值为负数图结构。而最为好用的是使用堆优化的Dijstra算法。

(一)Dijkstra算法
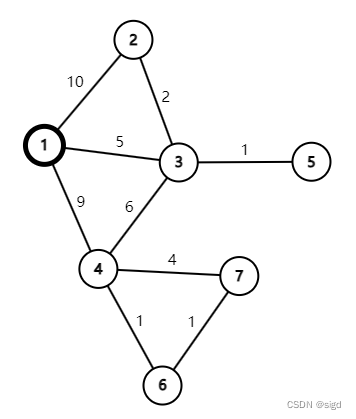
算法采用动态规划的思想,通过对图结构的递推,得到从点X出发,到其他所有结点的最短路径(不能处理边权为负值情况)。以下图为例,求结点1出发,到其余各结点最短路径。
(1)先找到从1出发的邻接点有(2,3,4),最短的边是(1,3,长度5),此时可以断言结点1到结点3最短路径是5。证明也很容易,因为其他路径必须先经过(1,2,长度10)或者(1,4,长度9)那么其长度必然大于5。
(2)从3出发找寻到其他结点更短的路径,可以发现
5+(3,2,长度2)要比原来的(1,2,长度10)更小,进行数据的更新;
5+(3,5,长度6)就不如原有的(1,4,长度9),不作更新操作;
5+(3,5,长度1)要比原来的(1,5,长度无穷大)更小,进行数据的更新。
更新全部之后选出最小的路径,此时为(1,3,2)长度7,此路径为结点1到结点2的最短路径。然后从结点2出发继续找寻到其他结点更短的路径。
算法实现细节:(1)用v数组标记已经求出最短路径的结点;(2)用d数组记录最短路径长度,通过迭代方式更新d数组,找到当前最短路径结点。
邻接表存储的算法实现。
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int n,m,v[105],d[105];
struct node
{int adj,val;
};
vector<node>e[105];
int getMin()
{int mini=0,i;for(i=1;i<=n;i++)if(v[i]==0&&d[i]<d[mini])mini=i;return mini;
}
void djstra(int s)
{int i,j;memset(d,127/3,sizeof(d));/**< 初始化d数组 */d[s]=0;/**< s为起点 */for(i=1; i<=n; i++){int temp=getMin();v[temp]=1;for(j=0; j<e[temp].size(); j++) /**< e[1] 存的是2 4 5,e[1][j] */{int x=e[temp][j].adj,z=e[temp][j].val;if(v[x]==0&&d[x]>d[temp]+z)d[x]=d[temp]+z;}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,ans=0;cin>>n>>m;for(i=1; i<=m; i++){cin>>x>>y>>z;e[x].push_back({y,z});e[y].push_back({x,z});}djstra(1);if(d[n]<1e8)cout<<d[n];elsecout<<-1;return 0;
}
邻接表用堆优化的算法
#include <iostream>
#include<cstring>
#include <queue>
#include<vector>
typedef long long ll;
using namespace std;
int n,m,v[105],d[105];
struct node
{int adj,val;bool operator<(const node B)const/**< 重载操作符,用于优先队列排序 */{return val>B.val;}
};
vector<node>e[105];
priority_queue<node>pq;
int getMin()/**< 用堆之后查找复杂度降为log级别 */
{while(pq.size()&&v[pq.top().adj])/**< 存在堆顶元素已经访问的情况 */pq.pop();int v=pq.top().adj;pq.pop();return v;
}
void djstra(int s)
{int i,j;memset(d,127/3,sizeof(d));/**< 初始化d数组 */d[s]=0;/**< s为起点 */for(i=1; i<=n; i++)/**< 初始化优先队列,放入结点i和对应的d[i],这里只是借用node类型,这两个值可不是邻接点和权值(正常来说需要再定义一个结构体类型) */pq.push({i,d[i]});for(i=1; i<=n; i++){int temp=getMin();v[temp]=1;for(j=0; j<e[temp].size(); j++) /**< e[1] 存的是2 4 5,e[1][j] */{int x=e[temp][j].adj,z=e[temp][j].val;if(v[x]==0&&d[x]>d[temp]+z)d[x]=d[temp]+z,pq.push({x,d[x]});}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,ans=0;cin>>n>>m;for(i=1; i<=m; i++){cin>>x>>y>>z;e[x].push_back({y,z});e[y].push_back({x,z});}djstra(1);if(d[n]<1e8)cout<<d[n];elsecout<<-1;return 0;
}
(二)Floyd算法
必须使用邻接矩阵存储结构。基于动态规划思想,通过n个点的拉伸得到任意两点最短路径。检查每一个结点k,试探能否通过k为中间结点减少结点i和j的最短路径长度。Floyd算法时间复杂度较高O(n3),但是能用于求任意两点最短路径。算法简单,只适用于结点数较少的情况。
#include <iostream>
#include <cstring>
typedef long long ll;
using namespace std;
int n,m,a[105][105];
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,k,x,y,z;cin>>n>>m;memset(a,127/3,sizeof(a));for(i=1;i<=m;i++){cin>>x>>y>>z;/**< 必须无向图 */a[x][y]=a[y][x]=z;}for(k=1;k<=n;k++){for(i=1;i<=n;i++){for(j=1;j<=n;j++){if(a[i][j]>a[i][k]+a[k][j])/**< 检查以k为中间点,是否能减少i和j的路径长度 */a[i][j]=a[i][k]+a[k][j];}}}if(a[1][n]>9999999)cout<<-1;elsecout<<a[1][n];return 0;
}
(三)SPFA算法
SPFA算法写起来和BFS算法几乎一模一样,也被称为队列优化算法,通常用于求含负权边的单源最短路径,以及判负权环。其处理过程和迪杰斯特拉区别在于,迪杰斯特拉算法需要找到最小的那个结点,而SPFA不管那些,只要一个结点的当前路径长度低于之前已有的值,那么就送入队列,因为新的路径长度可能刷新其他结点的最短路径长度。
#include <iostream>
#include <string.h>
#include<vector>
#include<queue>
typedef long long ll;
using namespace std;
int n,m,v[100005],d[100005];/**< V表示结点是否在队列中 */
vector< pair<int,int> > e[100005];
void spfa(int x)
{int i,temp;d[x]=0;queue<int>q;q.push(x);/**< 起点入队 */while(!q.empty()){temp=q.front();/**< temp出队结点,如果一个结点会反复入队出队超过n次,那么有负环存在 */q.pop();v[temp]=0;/**< 修改标志,未来可能会再次入队 */for(i=0;i<e[temp].size();i++){int y=e[temp][i].first,z=e[temp][i].second;if(d[y]>d[temp]+z) /**< y结点的路径长度变短 */{d[y]=d[temp]+z;if(v[y]==0)/**< 如果y结点此时不在队列中,加入队列中 */{q.push(y);v[y]=1;/**< 标记一下,假如在y出来之前又一次d[y]>d[temp]+z,那么也不用重复入队 */}}}}
}
int main()
{ios::sync_with_stdio(0),cin.tie(0);int i,j,x,y,z,s;cin>>n>>m;for(i=1;i<=m;i++){cin>>x>>y>>z;if(x==y)continue;e[x].push_back({y,z});e[y].push_back({x,z});}memset(d,127,sizeof(d));spfa(1);cout<<(d[n]>9999999?-1:d[n]);return 0;
}
