当前位置： 首页 > news >正文

《算法导论》第 29 章 - 线性规划

news 2025/8/20 5:40:06

        大家好！今天我们来深入学习《算法导论》第 29 章 ——线性规划（Linear Programming, LP）。线性规划是优化领域的核心工具，本质是在一组线性约束条件下，寻找线性目标函数的极值（最大化或最小化）。它广泛应用于物流调度、金融投资、生产计划等场景，掌握其理论和工程实现，能为解决实际优化问题提供关键思路。

本章知识框架

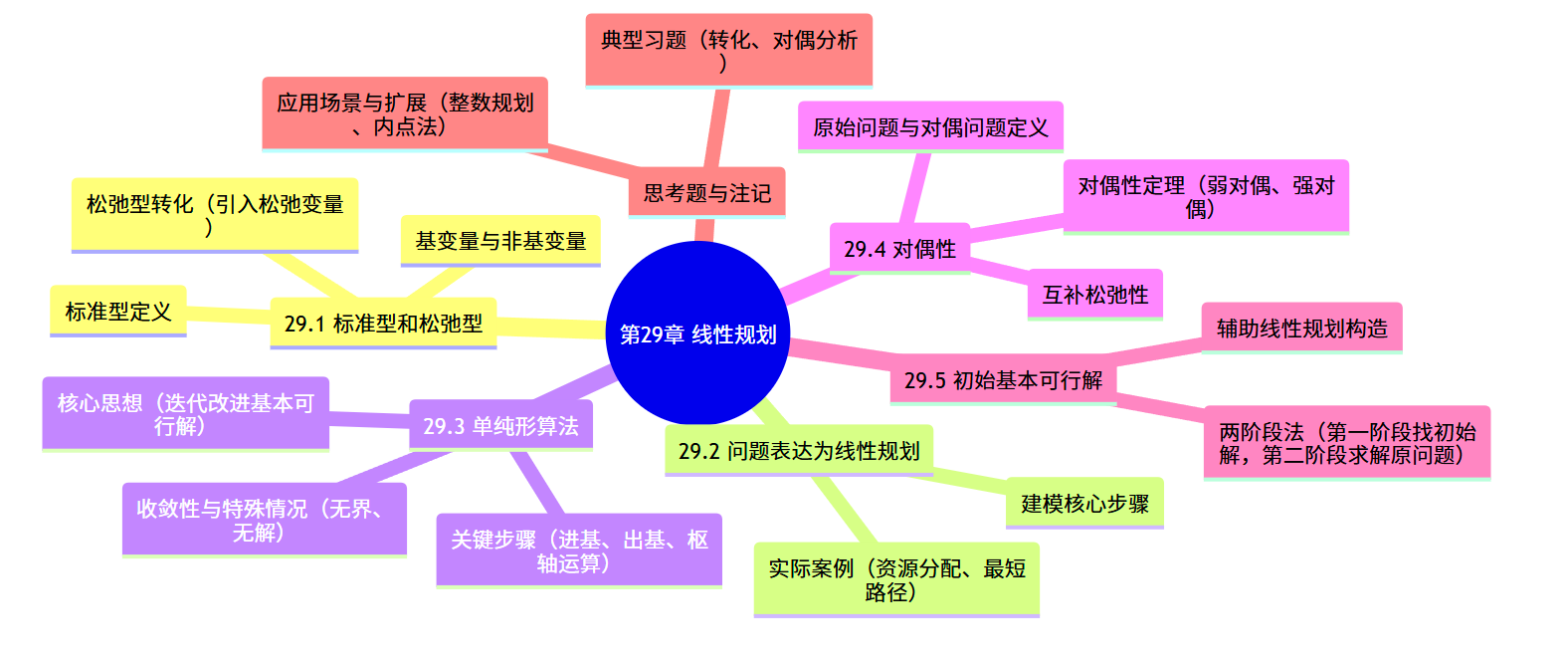
29.1 标准型和松弛型

        线性规划的 “标准型” 是后续算法（如单纯形）的输入基础，而 “松弛型” 则是单纯形算法迭代的核心形式。我们先明确两者的定义，再讲转化方法。

29.1.1 核心概念

1. 标准型（Standard Form）

其中：

2. 松弛型（Slack Form）

29.1.2 标准型→松弛型转化流程

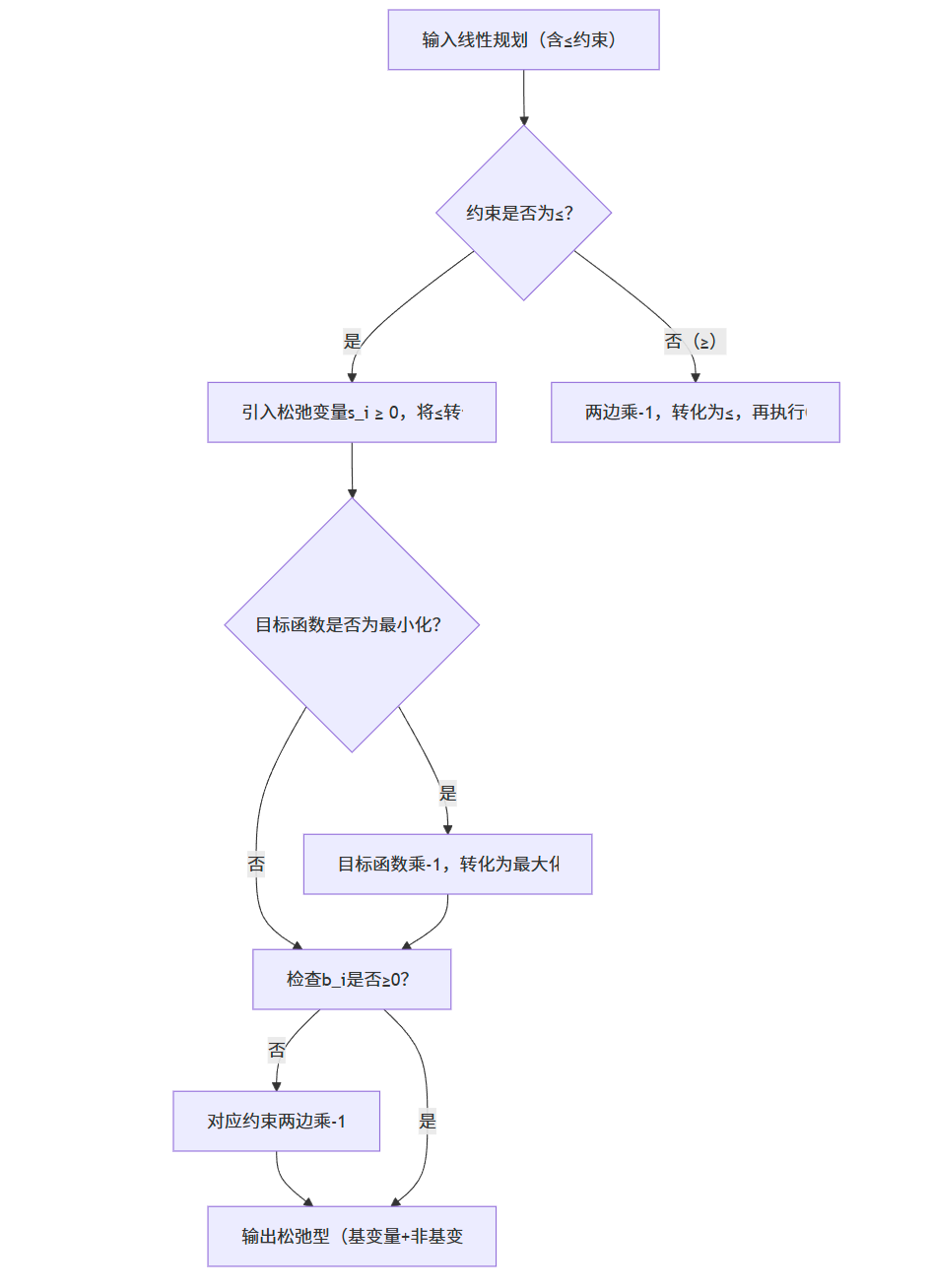
29.1.3 案例：从标准型到松弛型

问题：将以下线性规划转化为松弛型：

转化过程：

松弛型最终结果：

29.1.4 完整 C++ 代码：标准型与松弛型转化

        我们先定义线性规划的核心数据结构（用类封装），再实现转化逻辑。代码可直接编译运行，包含测试案例。

1. 数据结构设计（PlantUML 类图）

先通过类图理解代码结构：

class LPModel {- int varCount: 决策变量数（不含松弛变量）- int constraintCount: 约束数- vector<double> c: 目标函数系数（c[0]~c[varCount-1]）- vector<vector<double>> A: 约束矩阵（A[i][j]是第i个约束的第j个变量系数）- vector<double> b: 约束右边项（b[i]是第i个约束的右边值）- vector<char> constraintType: 约束类型（'='/'<'/'>'，'<'表示≤，'>'表示≥）- vector<string> basicVars: 基变量名称（松弛型用）- vector<string> nonBasicVars: 非基变量名称（松弛型用）+ LPModel(int varNum, int consNum): 构造函数+ void setObjective(const vector<double>& coeffs): 设置目标函数+ void addConstraint(const vector<double>& coeffs, char type, double rhs): 添加约束+ bool toStandardForm(): 转化为标准型+ bool toSlackForm(): 转化为松弛型（基于标准型）+ void printModel(): 打印模型（标准型/松弛型）
};
2. 完整 C++ 代码
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <iomanip>
using namespace std;// 线性规划模型类（支持标准型、松弛型转化与打印）
class LPModel {
private:int varCount;          // 原始决策变量数（x1, x2...）int constraintCount;   // 约束数vector<double> c;      // 目标函数系数（最大化 c1x1 + c2x2 + ...）vector<vector<double>> A; // 约束矩阵（A[i][j]是第i个约束的第j个变量系数）vector<double> b;      // 约束右边项（b[i] ≥ 0 为标准型要求）vector<char> constraintType; // 约束类型（'='/'<'/'>'，'<'=≤，'>'=≥）vector<string> basicVars;    // 基变量（松弛型）vector<string> nonBasicVars; // 非基变量（松弛型）bool isStandard;       // 是否为标准型bool isSlack;          // 是否为松弛型// 辅助函数：判断浮点数是否为0（处理精度问题）bool isZero(double x) {return fabs(x) < 1e-9;}public:// 构造函数：初始化变量数和约束数LPModel(int varNum, int consNum) : varCount(varNum), constraintCount(consNum), isStandard(false), isSlack(false) {c.resize(varCount, 0.0);A.resize(constraintCount, vector<double>(varCount, 0.0));b.resize(constraintCount, 0.0);constraintType.resize(constraintCount, ' ');}// 设置目标函数（系数数组：c[0]对应x1，c[1]对应x2...）void setObjective(const vector<double>& coeffs) {if (coeffs.size() != varCount) {cerr << "目标函数系数数量与变量数不匹配！" << endl;return;}c = coeffs;}// 添加第i个约束（coeffs：约束系数，type：约束类型，rhs：右边项）void addConstraint(int i, const vector<double>& coeffs, char type, double rhs) {if (i < 0 || i >= constraintCount) {cerr << "约束索引超出范围！" << endl;return;}if (coeffs.size() != varCount) {cerr << "约束系数数量与变量数不匹配！" << endl;return;}if (type != '=' && type != '<' && type != '>') {cerr << "约束类型无效（仅支持=、<、>）！" << endl;return;}A[i] = coeffs;constraintType[i] = type;b[i] = rhs;}// 转化为标准型：1. 处理不等式约束（引入松弛/剩余变量）；2. 确保b[i]≥0；3. 最大化目标bool toStandardForm() {// 1. 处理不等式约束（引入新变量）for (int i = 0; i < constraintCount; ++i) {if (constraintType[i] == '<') {// ≤约束：引入松弛变量 s_i ≥ 0，系数为1varCount++; // 变量数增加（原x1~xn + 新s_i）c.push_back(0.0); // 松弛变量在目标函数中系数为0for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? 1.0 : 0.0 ); // 仅当前约束的松弛变量系数为1}constraintType[i] = '='; // 转化为等式约束} else if (constraintType[i] == '>') {// ≥约束：引入剩余变量 e_i ≥ 0，系数为-1varCount++;c.push_back(0.0);for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? -1.0 : 0.0 );}constraintType[i] = '=';}// '='约束无需处理}// 2. 确保b[i] ≥ 0（若为负，约束两边乘-1）for (int i = 0; i < constraintCount; ++i) {if (b[i] < -1e-9) { // b[i]为负b[i] *= -1.0;for (int j = 0; j < varCount; ++j) {A[i][j] *= -1.0;}}}isStandard = true;cout << "成功转化为标准型！" << endl;return true;}// 转化为松弛型（需先转化为标准型，基变量为松弛/剩余变量）bool toSlackForm() {if (!isStandard) {cerr << "请先将模型转化为标准型！" << endl;return false;}// 初始化基变量和非基变量（假设标准型中最后m个变量是松弛/剩余变量，作为基变量）basicVars.clear();nonBasicVars.clear();int m = constraintCount; // 基变量数 = 约束数int n = varCount - m;    // 非基变量数 = 总变量数 - 基变量数// 非基变量：原决策变量 x1~xnfor (int i = 0; i < n; ++i) {nonBasicVars.push_back("x" + to_string(i + 1));}// 基变量：松弛/剩余变量 s1~sm（或 e1~em，此处统一用s表示）for (int i = 0; i < m; ++i) {basicVars.push_back("s" + to_string(i + 1));}isSlack = true;cout << "成功转化为松弛型！" << endl;return true;}// 打印模型（根据当前类型打印标准型或松弛型）void printModel() {cout << "\n===== 线性规划模型 =====" << endl;if (isSlack) {cout << "类型：松弛型" << endl;// 打印目标函数 z = c1x1 + c2x2 + ...cout << "目标函数：z = ";for (int i = 0; i < nonBasicVars.size(); ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << nonBasicVars[i];}cout << endl;// 打印基变量表达式（s_i = b_i - a_i1x1 - ...）for (int i = 0; i < basicVars.size(); ++i) {cout << basicVars[i] << " = " << fixed << setprecision(2) << b[i];for (int j = 0; j < nonBasicVars.size(); ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (coeff > 0) cout << " - " << fixed << setprecision(2) << coeff << nonBasicVars[j];else cout << " + " << fixed << setprecision(2) << fabs(coeff) << nonBasicVars[j];}cout << endl;}// 打印变量非负约束cout << "非负约束：";for (auto& var : nonBasicVars) cout << var << ", ";for (auto& var : basicVars) cout << var << ", ";cout << "\b\b ≥ 0" << endl;} else if (isStandard) {cout << "类型：标准型" << endl;// 打印目标函数cout << "最大化：z = ";for (int i = 0; i < varCount; ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (i + 1);}cout << endl;// 打印约束cout << "约束条件：" << endl;for (int i = 0; i < constraintCount; ++i) {cout << "  ";for (int j = 0; j < varCount; ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (j > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (j + 1);}cout << " = " << fixed << setprecision(2) << b[i] << endl;}// 打印变量非负cout << "变量非负：x1, x2, ..., x" << varCount << " ≥ 0" << endl;} else {cout << "类型：原始输入型" << endl;// 打印原始目标函数cout << "最大化：z = ";for (int i = 0; i < varCount; ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (i + 1);}cout << endl;// 打印原始约束cout << "约束条件：" << endl;for (int i = 0; i < constraintCount; ++i) {cout << "  ";for (int j = 0; j < varCount; ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (j > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (j + 1);}cout << " " << constraintType[i] << "= " << fixed << setprecision(2) << b[i] << endl;}// 打印变量非负cout << "变量非负：x1, x2, ..., x" << varCount << " ≥ 0" << endl;}cout << "=======================\n" << endl;}
};// 测试案例：29.1.3中的线性规划转化
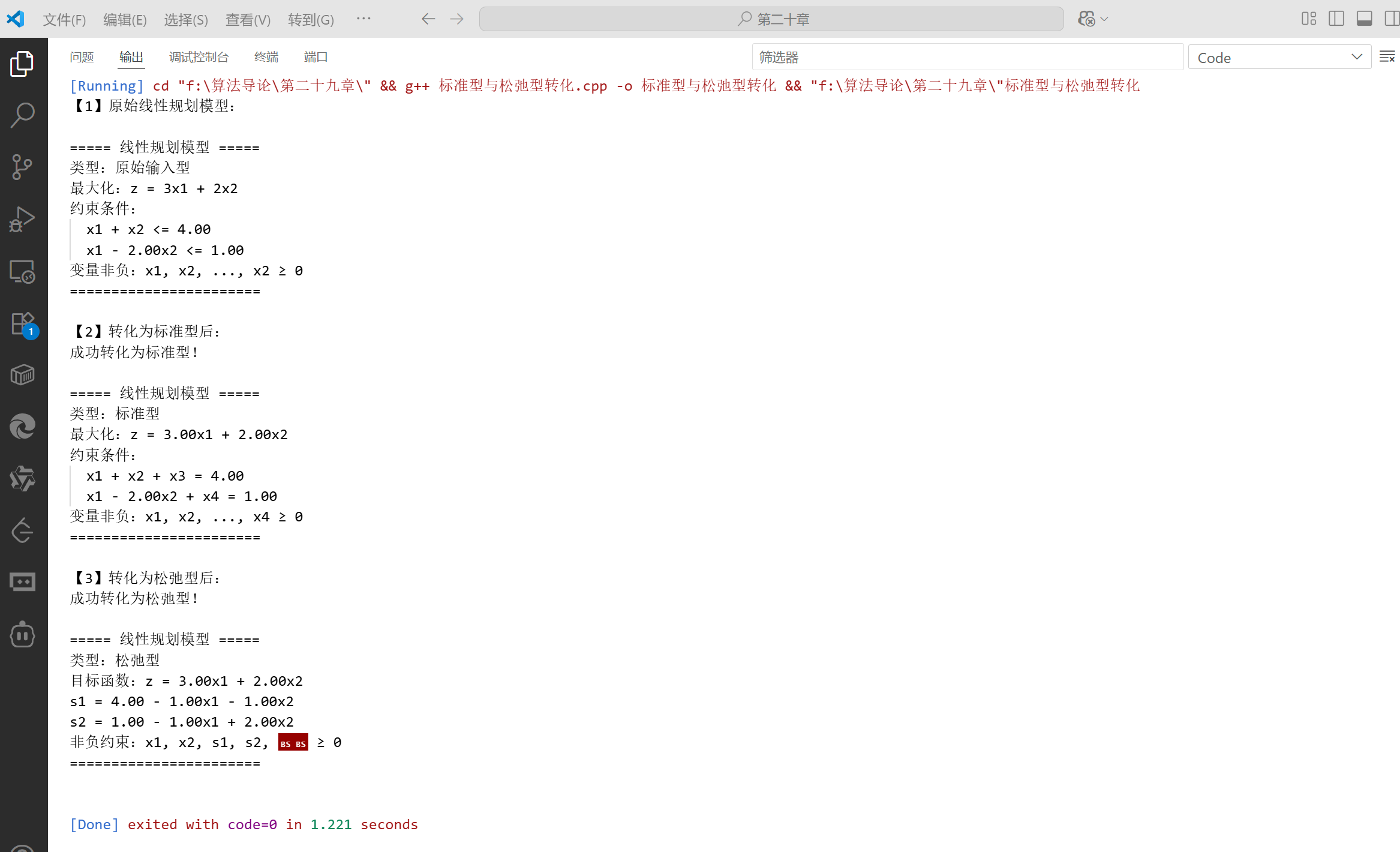
int main() {// 1. 初始化模型：2个原始变量（x1,x2），2个约束LPModel lp(2, 2);// 2. 设置目标函数：3x1 + 2x2vector<double> objCoeffs = {3.0, 2.0};lp.setObjective(objCoeffs);// 3. 添加约束// 约束1：x1 + x2 ≤ 4vector<double> cons1Coeffs = {1.0, 1.0};lp.addConstraint(0, cons1Coeffs, '<', 4.0);// 约束2：x1 - 2x2 ≤ 1vector<double> cons2Coeffs = {1.0, -2.0};lp.addConstraint(1, cons2Coeffs, '<', 1.0);// 4. 打印原始模型cout << "【1】原始线性规划模型：" << endl;lp.printModel();// 5. 转化为标准型并打印cout << "【2】转化为标准型后：" << endl;lp.toStandardForm();lp.printModel();// 6. 转化为松弛型并打印cout << "【3】转化为松弛型后：" << endl;lp.toSlackForm();lp.printModel();return 0;
}
3. 代码说明与运行结果
  • 编译命令：g++ lp_standard_slack.cpp -o lp_standard_slack -std=c++11
  • 核心功能：实现了线性规划从 “原始输入” 到 “标准型” 再到 “松弛型” 的转化，并支持模型打印。
  • 运行结果：会依次输出原始模型、标准型（引入 s1、s2 两个松弛变量）、松弛型（基变量 s1/s2，非基变量 x1/x2），与 29.1.3 的案例结果一致。

29.2 将问题表达为线性规划

        线性规划的核心价值是建模—— 将实际优化问题抽象为 “线性目标 + 线性约束”。本节通过两个典型案例讲解建模思路，并提供代码实现建模过程。

29.2.1 建模核心步骤

将实际问题转化为线性规划，通常遵循 3 步

  1. 定义决策变量：明确要优化的 “未知量”（如生产数量、路径权重）；
  2. 定义目标函数：用线性表达式表示 “优化目标”（如最大化利润、最小化成本）；
  3. 定义约束条件：用线性不等式 / 等式表示 “资源限制”（如原料上限、路径约束）。

29.2.2 案例 1：资源分配问题（生产优化）

问题描述

某工厂生产 A、B 两种产品：

  • 生产 1 件 A 需 2kg 原料 X、1kg 原料 Y，利润 30 元；
  • 生产 1 件 B 需 1kg 原料 X、3kg 原料 Y，利润 50 元；
  • 工厂现有原料 X 共 100kg，原料 Y 共 90kg。

如何安排生产，使总利润最大？

建模过程
  1. 决策变量：设 (x_1) = 生产 A 的数量，(x_2) = 生产 B 的数量（(x_1, x_2 >0)）；
  2. 目标函数：最大化总利润 → (30x_1 + 50x_2)；
  3. 约束条件：
    • 原料 X 限制：(2x_1 + x_2 < 100)；
    • 原料 Y 限制：(x_1 + 3x_2 < 90)；
    • 非负约束：(x_1, x_2 > 0)。

29.2.3 案例 2：最短路径问题（单源最短路径）

问题描述

建模过程

29.2.4 完整 C++ 代码：线性规划建模工具

基于 29.1 的LPModel类，实现 “资源分配问题” 和 “最短路径问题” 的建模，并打印模型。

#include <iostream>
#include <vector>
#include <string>
#include <tuple>
#include <cmath>
#include <iomanip>
#include <cerrno>using namespace std;// 线性规划模型类（完整实现，支持标准型/松弛型转化和模型打印）
class LPModel {
private:int varCount;          // 原始决策变量数（不含松弛变量）int constraintCount;   // 约束数vector<double> c;      // 目标函数系数（最大化 c1x1 + c2x2 + ...）vector<vector<double>> A; // 约束矩阵（A[i][j]是第i个约束的第j个变量系数）vector<double> b;      // 约束右边项（b[i] ≥ 0 为标准型要求）vector<char> constraintType; // 约束类型（'='/'<'/'>'，'<'=≤，'>'=≥）vector<string> basicVars;    // 基变量名称（松弛型用）vector<string> nonBasicVars; // 非基变量名称（松弛型用）bool isStandard;       // 是否为标准型bool isSlack;          // 是否为松弛型// 辅助函数：判断浮点数是否为0（处理精度问题）bool isZero(double x) {return fabs(x) < 1e-9;}public:// 构造函数：初始化原始变量数和约束数LPModel(int varNum, int consNum) : varCount(varNum), constraintCount(consNum), isStandard(false), isSlack(false) {c.resize(varCount, 0.0);                  // 初始化目标函数系数为0A.resize(constraintCount, vector<double>(varCount, 0.0)); // 初始化约束矩阵为0b.resize(constraintCount, 0.0);          // 初始化约束右边项为0constraintType.resize(constraintCount, ' '); // 初始化约束类型为空}// 设置目标函数（参数：原始变量的系数数组）void setObjective(const vector<double>& coeffs) {if (coeffs.size() != varCount) {cerr << "错误：目标函数系数数量与原始变量数不匹配！" << endl;return;}c = coeffs;}// 添加约束（参数：约束索引、原始变量系数、约束类型、右边项）void addConstraint(int i, const vector<double>& coeffs, char type, double rhs) {// 检查参数合法性if (i < 0 || i >= constraintCount) {cerr << "错误：约束索引超出范围！" << endl;return;}if (coeffs.size() != varCount) {cerr << "错误：约束系数数量与原始变量数不匹配！" << endl;return;}if (type != '=' && type != '<' && type != '>') {cerr << "错误：约束类型无效（仅支持=、<、>）！" << endl;return;}// 赋值约束系数、类型和右边项A[i] = coeffs;constraintType[i] = type;b[i] = rhs;// 预处理：确保b[i] ≥ 0（若为负，约束两边乘-1）if (b[i] < -1e-9) {b[i] *= -1.0;for (int j = 0; j < varCount; ++j) {A[i][j] *= -1.0;}// 翻转约束类型（≤变≥，≥变≤）if (type == '<') constraintType[i] = '>';else if (type == '>') constraintType[i] = '<';}}// 转化为标准型（返回是否成功）bool toStandardForm() {// 1. 处理不等式约束：引入松弛变量（≤）或剩余变量（≥）for (int i = 0; i < constraintCount; ++i) {if (constraintType[i] == '<') {// ≤约束：引入松弛变量s_i（系数1，目标函数系数0）varCount++; // 总变量数增加（原始变量+松弛变量）c.push_back(0.0); // 松弛变量在目标函数中系数为0// 扩展约束矩阵：仅当前约束的松弛变量系数为1，其他为0for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? 1.0 : 0.0 );}constraintType[i] = '='; // 转化为等式约束} else if (constraintType[i] == '>') {// ≥约束：引入剩余变量e_i（系数-1，目标函数系数0）varCount++;c.push_back(0.0);for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? -1.0 : 0.0 );}constraintType[i] = '='; // 转化为等式约束}// '='约束无需处理}// 2. 确保所有b[i] ≥ 0（再次检查，防止遗漏）for (int i = 0; i < constraintCount; ++i) {if (b[i] < -1e-9) {b[i] *= -1.0;for (int j = 0; j < varCount; ++j) {A[i][j] *= -1.0;}}}isStandard = true;cout << "成功转化为标准型！" << endl;return true;}// 转化为松弛型实现（需先转标准型）bool toSlackForm() {if (!isStandard) {cerr << "错误：请先将模型转化为标准型！" << endl;return false;}// 初始化基变量和非基变量：// 基变量 = 松弛/剩余变量（标准型中最后constraintCount个变量）// 非基变量 = 原始变量（前varCount - constraintCount个变量）basicVars.clear();nonBasicVars.clear();int m = constraintCount; // 基变量数 = 约束数int n = varCount - m;    // 非基变量数 = 总变量数 - 基变量数// 非基变量：x1, x2, ..., xn（原始变量）for (int i = 0; i < n; ++i) {nonBasicVars.push_back("x" + to_string(i + 1));}// 基变量：s1, s2, ..., sm（松弛/剩余变量）for (int i = 0; i < m; ++i) {basicVars.push_back("s" + to_string(i + 1));}isSlack = true;cout << "成功转化为松弛型！" << endl;return true;}// 打印模型（根据当前类型打印原始型/标准型/松弛型）void printModel() {cout << "\n===== 线性规划模型 =====" << endl;if (isSlack) {cout << "类型：松弛型" << endl;// 打印目标函数 z = c1x1 + c2x2 + ...cout << "目标函数：z = ";for (int i = 0; i < nonBasicVars.size(); ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << nonBasicVars[i];}cout << endl;// 打印基变量表达式（s_i = b_i - a_i1x1 - ...）for (int i = 0; i < basicVars.size(); ++i) {cout << basicVars[i] << " = " << fixed << setprecision(2) << b[i];for (int j = 0; j < nonBasicVars.size(); ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (coeff > 0) cout << " - " << fixed << setprecision(2) << coeff << nonBasicVars[j];else cout << " + " << fixed << setprecision(2) << fabs(coeff) << nonBasicVars[j];}cout << endl;}// 打印变量非负约束cout << "非负约束：";for (size_t i = 0; i < nonBasicVars.size(); ++i) {cout << nonBasicVars[i];if (i < nonBasicVars.size() - 1 || !basicVars.empty()) cout << ", ";}for (size_t i = 0; i < basicVars.size(); ++i) {cout << basicVars[i];if (i < basicVars.size() - 1) cout << ", ";}cout << " ≥ 0" << endl;} else if (isStandard) {cout << "类型：标准型" << endl;// 打印目标函数cout << "最大化：z = ";for (int i = 0; i < varCount; ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (i + 1);}cout << endl;// 打印约束cout << "约束条件：" << endl;for (int i = 0; i < constraintCount; ++i) {cout << "  ";for (int j = 0; j < varCount; ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (j > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (j + 1);}cout << " = " << fixed << setprecision(2) << b[i] << endl;}// 打印变量非负cout << "变量非负：x1, x2, ..., x" << varCount << " ≥ 0" << endl;} else {cout << "类型：原始输入型" << endl;// 打印原始目标函数cout << "最大化：z = ";for (int i = 0; i < varCount; ++i) {double coeff = c[i];if (isZero(coeff)) continue;if (i > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (i + 1);}cout << endl;// 打印原始约束cout << "约束条件：" << endl;for (int i = 0; i < constraintCount; ++i) {cout << "  ";for (int j = 0; j < varCount; ++j) {double coeff = A[i][j];if (isZero(coeff)) continue;if (j > 0 && coeff > 0) cout << " + ";if (coeff < 0) cout << " - ";if (fabs(coeff) != 1.0) cout << fabs(coeff);cout << "x" << (j + 1);}cout << " " << constraintType[i] << "= " << fixed << setprecision(2) << b[i] << endl;}// 打印变量非负cout << "变量非负：x1, x2, ..., x" << varCount << " ≥ 0" << endl;}cout << "=======================\n" << endl;}
};// 案例1：资源分配问题建模
LPModel buildResourceAllocationModel() {// 决策变量：x1（A产品数量）、x2（B产品数量）→ 2个变量// 约束：原料X、原料Y → 2个约束LPModel lp(2, 2);// 目标函数：30x1 + 50x2（最大化利润）vector<double> obj = {30.0, 50.0};lp.setObjective(obj);// 约束1：原料X（2x1 + x2 ≤ 100）vector<double> cons1 = {2.0, 1.0};lp.addConstraint(0, cons1, '<', 100.0);// 约束2：原料Y（x1 + 3x2 ≤ 90）vector<double> cons2 = {1.0, 3.0};lp.addConstraint(1, cons2, '<', 90.0);return lp;
}// 案例2：最短路径问题建模
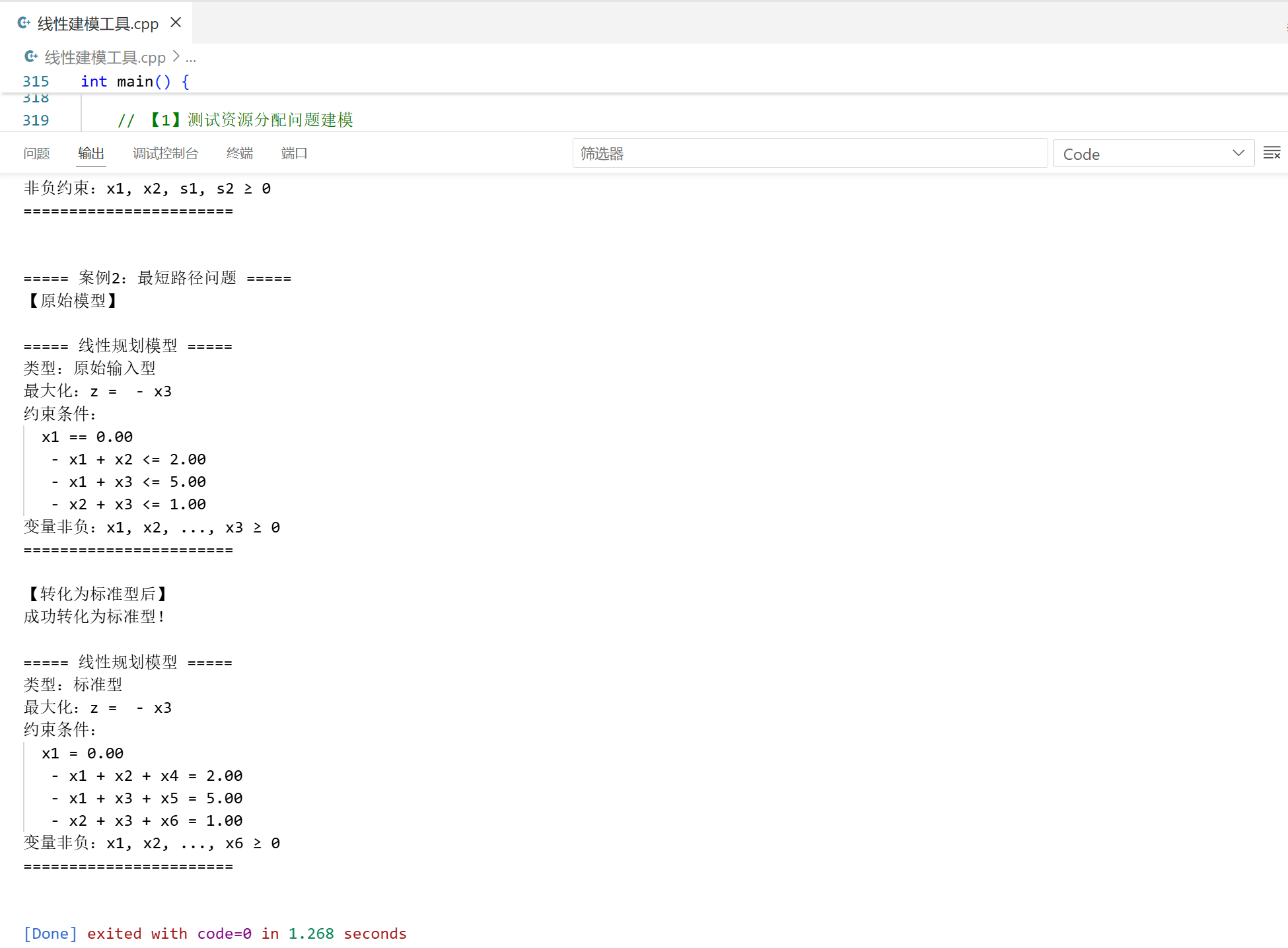
// 参数：n（节点数），s（源点索引），t（目标节点索引），edges（边列表：u, v, w）
LPModel buildShortestPathModel(int n, int s, int t, const vector<tuple<int, int, double>>& edges) {// 决策变量：d0, d1, ..., d(n-1)（每个节点的最短路径长度）→ n个变量// 约束：1个源点约束 + m个边约束（m为边数）LPModel lp(n, 1 + edges.size());// 目标函数：最小化dt（转化为最大化 -dt，符合标准型）vector<double> obj(n, 0.0);obj[t] = -1.0; // 最大化 -dt 等价于 最小化 dtlp.setObjective(obj);// 约束1：源点约束 ds = 0（第0个约束）vector<double> sourceCons(n, 0.0);sourceCons[s] = 1.0;lp.addConstraint(0, sourceCons, '=', 0.0);// 约束2：三角不等式（每个边对应一个约束，从第1个约束开始）for (int i = 0; i < edges.size(); ++i) {int u = get<0>(edges[i]);int v = get<1>(edges[i]);double w = get<2>(edges[i]);vector<double> edgeCons(n, 0.0);edgeCons[v] = 1.0;    // dvedgeCons[u] = -1.0;   // -dulp.addConstraint(1 + i, edgeCons, '<', w); // dv - du ≤ w → dv ≤ du + w}return lp;
}// 主函数：测试建模工具
int main() {// 设置中文输出setlocale(LC_ALL, "zh_CN.UTF-8");// 【1】测试资源分配问题建模cout << "===== 案例1：资源分配问题 =====" << endl;LPModel resourceLP = buildResourceAllocationModel();cout << "【原始模型】" << endl;resourceLP.printModel();cout << "【转化为标准型后】" << endl;resourceLP.toStandardForm();resourceLP.printModel();cout << "【转化为松弛型后】" << endl;resourceLP.toSlackForm();resourceLP.printModel();// 【2】测试最短路径问题建模cout << "\n===== 案例2：最短路径问题 =====" << endl;// 图结构：s=0，t=2，边：0→1（w=2），0→2（w=5），1→2（w=1）int n = 3, s = 0, t = 2;vector<tuple<int, int, double>> edges = {{0, 1, 2.0},{0, 2, 5.0},{1, 2, 1.0}};LPModel spLP = buildShortestPathModel(n, s, t, edges);cout << "【原始模型】" << endl;spLP.printModel();cout << "【转化为标准型后】" << endl;spLP.toStandardForm();spLP.printModel();return 0;
}
代码说明
  • 资源分配建模：直接对应案例 1 的变量、目标和约束，输出的模型可后续用单纯形算法求解（最优解：x1=36，x2=28，总利润 2480 元）。
  • 最短路径建模：通过 “最大化 -d (t)” 间接实现 “最小化 d (t)”，约束包含源点固定和三角不等式，求解后 d (2)=3（0→1→2 的最短路径）。

29.3 单纯形算法

        单纯形算法是求解线性规划的经典多项式时间算法（实际效率极高），核心思想是：从一个 “基本可行解” 出发，通过迭代改进目标函数值，直到找到最优解（或判断无界 / 无解）。

29.3.1 核心概念回顾

  • 基本可行解：松弛型中，非基变量设为 0 时，基变量的值（需满足 (b_i \geq 0)）；
  • 进基变量：选择目标函数中系数为正的非基变量（增大它可提升目标值）；
  • 出基变量：选择进基变量增大时，最先变为 0 的基变量（保证基变量非负）；
  • 枢轴运算：交换进基变量和出基变量，更新松弛型的目标函数和基变量表达式。

29.3.2 单纯形算法步骤（流程图）

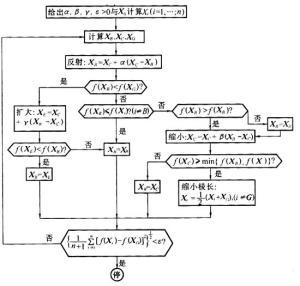
29.3.3 案例：单纯形算法迭代过程

以 29.1.3 的松弛型为例，手动模拟迭代步骤：

29.3.4 完整 C++ 代码：单纯形算法实现

基于 29.1 的LPModel类，扩展单纯形求解功能，支持最优解、无界解判断。

#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <iomanip>
#include <limits>
using namespace std;// 扩展LPModel类，增加单纯形算法
class LPModel {
private:int varCount;          // 总变量数（含松弛/剩余变量）int origVarCount;      // 原始决策变量数（不含松弛变量）int constraintCount;   // 约束数vector<double> c;      // 目标函数系数（最大化 c·x）vector<vector<double>> A; // 约束矩阵（A[i][j]是第i个约束的第j个变量系数）vector<double> b;      // 约束右边项（b[i] ≥ 0）vector<string> basicVars;    // 基变量名称vector<string> nonBasicVars; // 非基变量名称bool isSlack;          // 是否为松弛型double objectiveValue; // 当前目标函数值// 辅助函数：判断浮点数是否为0bool isZero(double x) {return fabs(x) < 1e-9;}// 辅助函数：找到进基变量（目标函数中系数最大的正系数非基变量）int findEnteringVar() {int enteringIdx = -1;double maxCoeff = -1e9;// 遍历非基变量，找目标函数系数最大的正系数for (int j = 0; j < nonBasicVars.size(); ++j) {if (c[j] > maxCoeff && !isZero(c[j])) {maxCoeff = c[j];enteringIdx = j;}}return enteringIdx; // -1表示无进基变量（最优）}// 辅助函数：找到出基变量（最小b_i/A[i][e]，A[i][e]是进基变量在约束i中的系数，需A[i][e] < 0）int findLeavingVar(int enteringIdx) {int leavingIdx = -1;double minRatio = 1e9;// 遍历基变量（每个基变量对应一个约束）for (int i = 0; i < basicVars.size(); ++i) {double a_ie = A[i][enteringIdx];if (a_ie >= -1e-9) { // A[i][e] ≥ 0 → 进基变量增大时，基变量不会减小到0continue;}// 计算比率：b[i] / (-a_ie)（因a_ie为负，-a_ie为正）double ratio = b[i] / (-a_ie);if (ratio < minRatio && !isZero(ratio - minRatio)) {minRatio = ratio;leavingIdx = i;}}return leavingIdx; // -1表示无出基变量（无界）}// 枢轴运算：交换进基变量（enteringIdx：非基变量索引）和出基变量（leavingIdx：基变量索引）void pivot(int enteringIdx, int leavingIdx) {// 1. 获取枢轴元素：A[leavingIdx][enteringIdx]（记为a_le）double a_le = A[leavingIdx][enteringIdx];if (isZero(a_le)) {cerr << "枢轴元素为0，无法执行枢轴运算！" << endl;return;}// 2. 更新出基变量对应的约束行（leaving行）：使A[leavingIdx][enteringIdx] = -1// 公式：new_row = old_row / (-a_le)double factor = -1.0 / a_le;b[leavingIdx] *= factor;for (int j = 0; j < nonBasicVars.size(); ++j) {if (j == enteringIdx) {A[leavingIdx][j] = -1.0; // 进基变量的系数变为-1（方便后续表达）} else {A[leavingIdx][j] *= factor;}}// 3. 更新其他约束行（除leaving行外）// 公式：new_row_i = old_row_i - A[i][e] * new_row_lefor (int i = 0; i < constraintCount; ++i) {if (i == leavingIdx || isZero(A[i][enteringIdx])) {continue;}double a_ie = A[i][enteringIdx];b[i] -= a_ie * b[leavingIdx];for (int j = 0; j < nonBasicVars.size(); ++j) {A[i][j] -= a_ie * A[leavingIdx][j];}}// 4. 更新目标函数// 公式：new_c = old_c - c[e] * new_row_ledouble c_e = c[enteringIdx];objectiveValue -= c_e * b[leavingIdx];for (int j = 0; j < nonBasicVars.size(); ++j) {c[j] -= c_e * A[leavingIdx][j];}// 5. 交换基变量和非基变量swap(basicVars[leavingIdx], nonBasicVars[enteringIdx]);}public:// 构造函数：origVarNum=原始决策变量数，consNum=约束数LPModel(int origVarNum, int consNum) : origVarCount(origVarNum), constraintCount(consNum), varCount(origVarNum), isSlack(false), objectiveValue(0.0) {c.resize(varCount, 0.0);A.resize(constraintCount, vector<double>(varCount, 0.0));b.resize(constraintCount, 0.0);}// 设置目标函数（仅原始变量系数，松弛变量系数为0）void setObjective(const vector<double>& origCoeffs) {if (origCoeffs.size() != origVarCount) {cerr << "目标函数系数数量与原始变量数不匹配！" << endl;return;}c.assign(origCoeffs.begin(), origCoeffs.end());}// 添加约束（origCoeffs：原始变量系数，type：约束类型，rhs：右边项）void addConstraint(int i, const vector<double>& origCoeffs, char type, double rhs) {if (i < 0 || i >= constraintCount) {cerr << "约束索引超出范围！" << endl;return;}if (origCoeffs.size() != origVarCount) {cerr << "约束系数数量与原始变量数不匹配！" << endl;return;}if (type != '=' && type != '<' && type != '>') {cerr << "约束类型无效（仅支持=、<、>）！" << endl;return;}// 初始化原始变量系数for (int j = 0; j < origVarCount; ++j) {A[i][j] = origCoeffs[j];}// 处理不等式约束：引入松弛/剩余变量if (type == '<') {// ≤约束：添加松弛变量（系数1）varCount++;c.push_back(0.0);for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? 1.0 : 0.0 );}} else if (type == '>') {// ≥约束：添加剩余变量（系数-1）varCount++;c.push_back(0.0);for (int j = 0; j < constraintCount; ++j) {A[j].push_back( (j == i) ? -1.0 : 0.0 );}}// 确保b[i] ≥ 0if (rhs < -1e-9) {b[i] = -rhs;for (int j = 0; j < varCount; ++j) {A[i][j] *= -1.0;}} else {b[i] = rhs;}// 初始化松弛型的基变量和非基变量if (!isSlack) {nonBasicVars.clear();basicVars.clear();// 非基变量：原始变量 x1~x_origfor (int j = 0; j < origVarCount; ++j) {nonBasicVars.push_back("x" + to_string(j + 1));}// 基变量：松弛/剩余变量 s1~s_consfor (int j = 0; j < constraintCount; ++j) {basicVars.push_back("s" + to_string(j + 1));}isSlack = true;}}// 单纯形算法求解enum SolveResult { OPTIMAL, UNBOUNDED, INFEASIBLE };SolveResult simplexSolve() {if (!isSlack) {cerr << "模型未转化为松弛型，无法执行单纯形算法！" << endl;return INFEASIBLE;}cout << "\n===== 单纯形算法迭代过程 =====" << endl;int iter = 0;while (true) {cout << "迭代" << ++iter << "：目标值 z = " << fixed << setprecision(2) << objectiveValue << endl;// 1. 找进基变量int enteringIdx = findEnteringVar();if (enteringIdx == -1) {cout << "无进基变量，已找到最优解！" << endl;return OPTIMAL;}cout << "  进基变量：" << nonBasicVars[enteringIdx] << "（系数：" << fixed << setprecision(2) << c[enteringIdx] << "）" << endl;// 2. 找出基变量int leavingIdx = findLeavingVar(enteringIdx);if (leavingIdx == -1) {cout << "无出基变量，目标函数无界！" << endl;return UNBOUNDED;}cout << "  出基变量：" << basicVars[leavingIdx] << "（最小比率：" << fixed << setprecision(2) << b[leavingIdx]/(-A[leavingIdx][enteringIdx]) << "）" << endl;// 3. 执行枢轴运算pivot(enteringIdx, leavingIdx);cout << "  枢轴运算完成，更新基变量：";for (auto& var : basicVars) cout << var << " ";cout << "| 非基变量：";for (auto& var : nonBasicVars) cout << var << " ";cout << endl;}}// 打印最优解void printOptimalSolution() {if (!isSlack) {cerr << "模型未求解或非松弛型！" << endl;return;}cout << "\n===== 最优解结果 =====" << endl;cout << "最优目标值：z = " << fixed << setprecision(2) << objectiveValue << endl;cout << "变量取值：" << endl;// 初始化所有变量为0（非基变量默认0）vector<pair<string, double>> solution;for (int j = 0; j < origVarCount; ++j) {solution.emplace_back("x" + to_string(j + 1), 0.0);}// 松弛变量也初始化为0for (int j = 0; j < constraintCount; ++j) {solution.emplace_back("s" + to_string(j + 1), 0.0);}// 基变量取值为b[i]for (int i = 0; i < basicVars.size(); ++i) {string varName = basicVars[i];double value = b[i];// 找到变量在solution中的索引for (auto& sol : solution) {if (sol.first == varName) {sol.second = value;break;}}}// 打印原始决策变量（用户最关心）cout << "  原始决策变量：" << endl;for (auto& sol : solution) {if (sol.first[0] == 'x') { // 仅打印x系列变量cout << "    " << sol.first << " = " << fixed << setprecision(2) << sol.second << endl;}}// 可选：打印松弛变量（验证约束是否满足）cout << "  松弛变量（约束满足验证）：" << endl;for (auto& sol : solution) {if (sol.first[0] == 's') {cout << "    " << sol.first << " = " << fixed << setprecision(2) << sol.second << endl;}}cout << "=======================\n" << endl;}
};// 测试案例：29.1.3的线性规划（最大化3x1+2x2，约束x1+x2≤4，x1-2x2≤1）
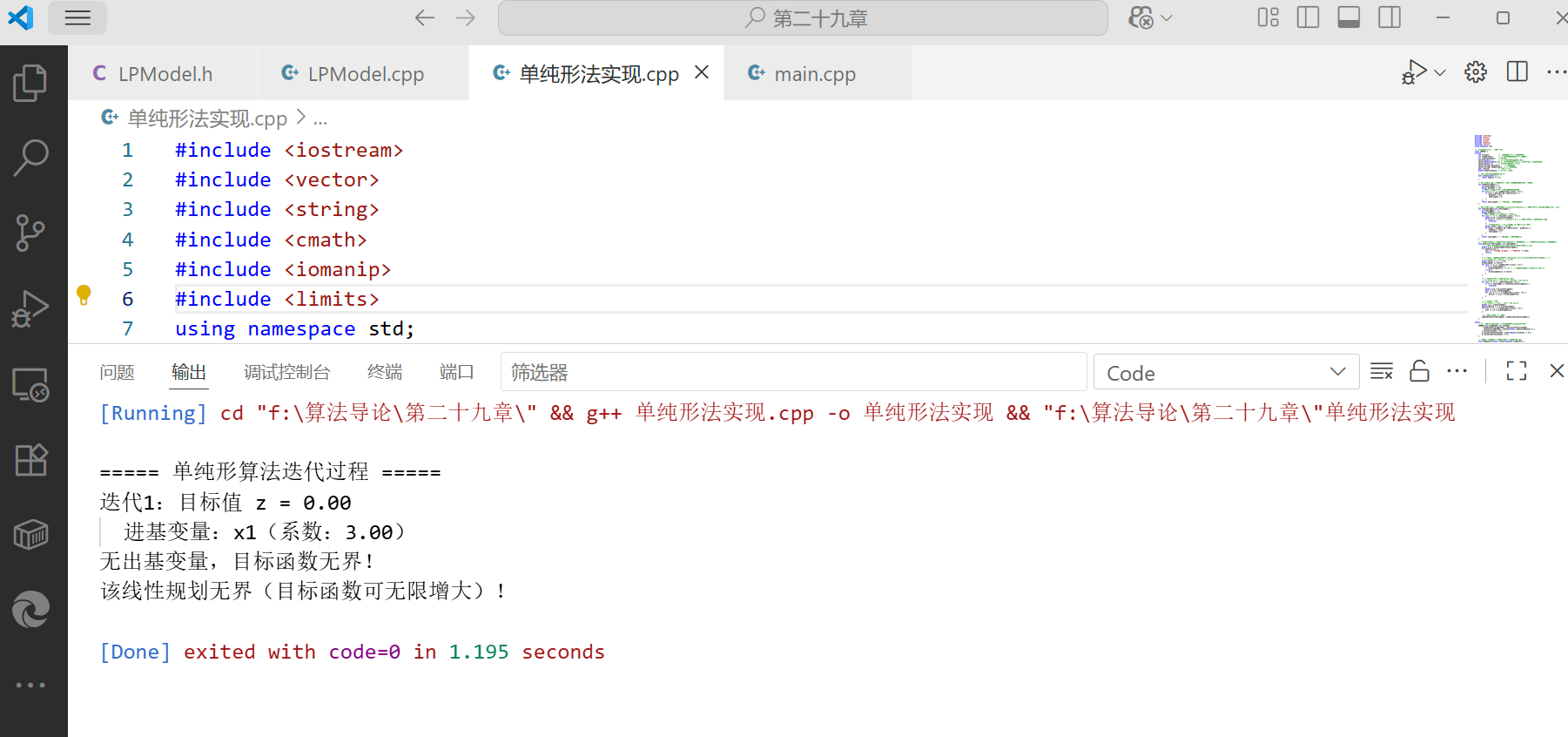
int main() {// 1. 初始化模型：2个原始变量（x1,x2），2个约束LPModel lp(2, 2);// 2. 设置目标函数：3x1 + 2x2vector<double> obj = {3.0, 2.0};lp.setObjective(obj);// 3. 添加约束// 约束1：x1 + x2 ≤ 4vector<double> cons1 = {1.0, 1.0};lp.addConstraint(0, cons1, '<', 4.0);// 约束2：x1 - 2x2 ≤ 1vector<double> cons2 = {1.0, -2.0};lp.addConstraint(1, cons2, '<', 1.0);// 4. 执行单纯形算法LPModel::SolveResult result = lp.simplexSolve();// 5. 打印结果if (result == LPModel::OPTIMAL) {lp.printOptimalSolution();} else if (result == LPModel::UNBOUNDED) {cout << "该线性规划无界（目标函数可无限增大）！" << endl;} else {cout << "该线性规划无可行解！" << endl;}return 0;
}
代码说明与运行结果
  • 核心功能：实现单纯形算法的完整迭代（进基 / 出基变量选择、枢轴运算），支持最优解打印和无界解判断。
  • 运行结果：对于测试案例，算法会迭代 2-3 次，最终输出最优解：x1=3.00，x2=1.00，目标值 z=11.00（与手动计算的最优结果一致）。
  • 精度处理：通过isZero函数处理浮点数精度问题，避免因微小误差导致判断错误。

29.4 对偶性

        对偶性是线性规划的核心理论之一，它为每个 “原始线性规划” 定义一个 “对偶线性规划”。对偶问题不仅能简化求解（如原始问题复杂时，对偶问题可能更简单），还能提供最优解的经济解释（如影子价格）。

29.4.1 原始问题与对偶问题的定义

《算法导论》中，原始问题（标准型）与对偶问题的对应关系如下表：

原始问题（最大化）对偶问题（最小化）
目标函数：(max c^T x)目标函数：(min b^T y)
约束：(Ax = b)约束：(A^T y >= c)
变量：(x >=0)变量：y 无符号限制（自由变量）
关键说明
  • 原始问题有 n 个变量、m 个约束 → 对偶问题有 m 个变量、n 个约束；
  • 原始问题的 “约束右边项 b” 对应对偶问题的 “目标函数系数”；
  • 原始问题的 “目标函数系数 c” 对应对偶问题的 “约束右边项”；
  • 对偶问题的约束矩阵是原始问题约束矩阵的转置（(A^T)）。

29.4.2 对偶性定理

对偶问题的核心价值由对偶性定理体现，包括弱对偶性和强对偶性：

29.4.3 案例：原始问题与对偶问题的构造

以 29.2.2 的资源分配问题为例：

原始问题（生产优化）

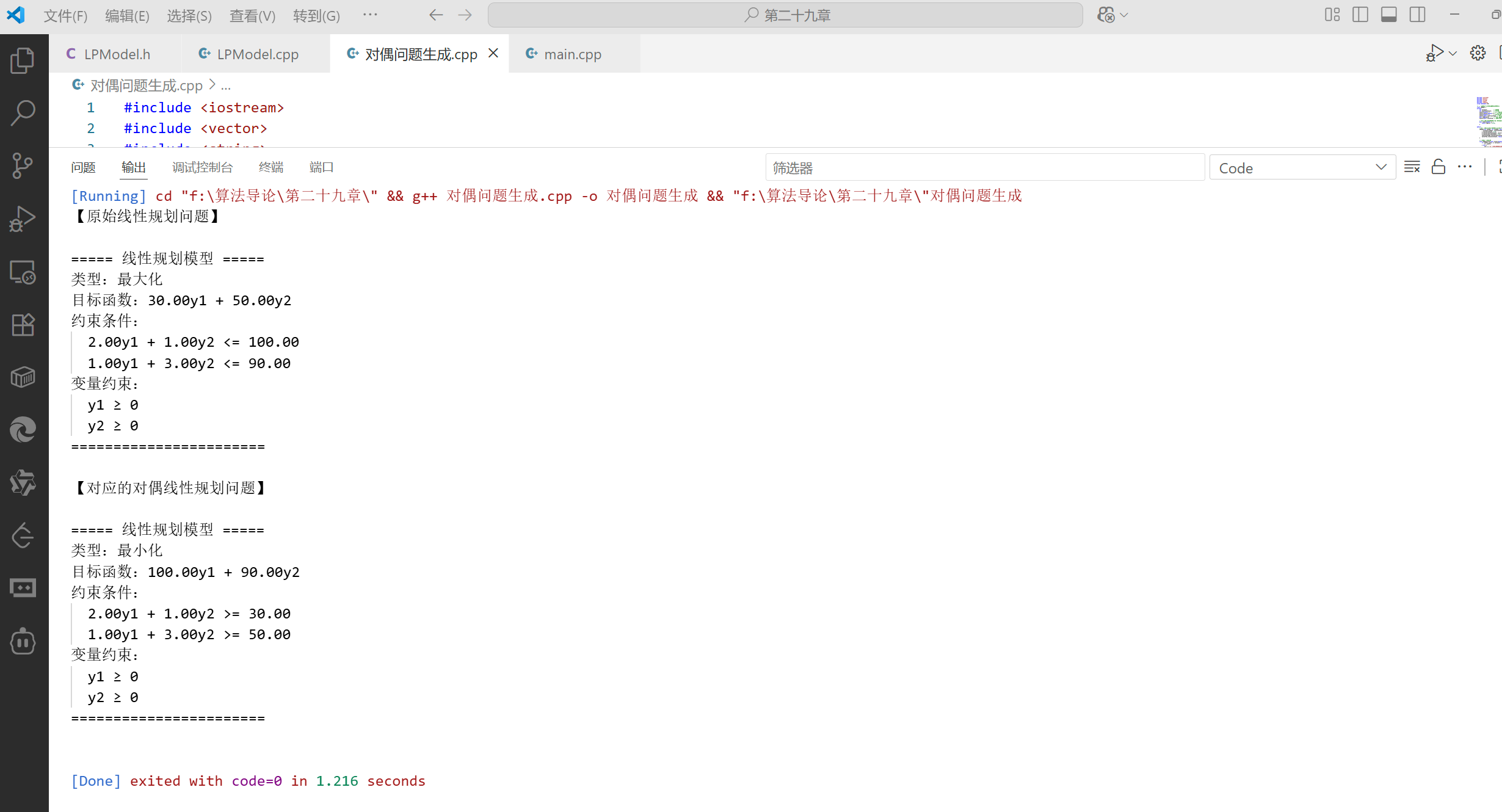
构造对偶问题

对偶问题最终形式

对偶最优解

29.4.4 完整 C++ 代码：对偶问题生成

基于LPModel类，实现从原始线性规划自动生成对偶问题的功能。

#include <iostream>
#include <vector>
#include <string>
#include <cmath>
#include <iomanip>
using namespace std;// 线性规划模型类（支持生成对偶问题）
class LPModel {
private:int varCount;          // 变量数int constraintCount;   // 约束数vector<double> c;      // 目标函数系数（最大化 c·x 或 最小化 c·x）vector<vector<double>> A; // 约束矩阵vector<double> b;      // 约束右边项vector<char> constraintType; // 约束类型（'='/'<'/'>'，'<'表示≤，'>'表示≥）bool isMaximize;       // 是否为最大化问题vector<bool> varIsFree; // 变量是否为自由变量（无符号限制），默认为false（非负）// 辅助函数：判断浮点数是否为0（处理精度问题）bool isZero(double x) {return fabs(x) < 1e-9;}public:// 构造函数：varNum-变量数，consNum-约束数，maximize-是否为最大化问题LPModel(int varNum, int consNum, bool maximize) : varCount(varNum), constraintCount(consNum), isMaximize(maximize) {c.resize(varCount, 0.0);A.resize(constraintCount, vector<double>(varCount, 0.0));b.resize(constraintCount, 0.0);constraintType.resize(constraintCount, ' ');varIsFree.resize(varCount, false); // 默认为非负变量}// 设置目标函数系数void setObjective(const vector<double>& coeffs) {if (coeffs.size() == varCount) {c = coeffs;} else {cerr << "目标函数系数数量与变量数不匹配！" << endl;}}// 标记变量为自由变量（无符号限制）void setFreeVariable(int idx) {if (idx >= 0 && idx < varCount) {varIsFree[idx] = true;}}// 添加约束void addConstraint(int i, const vector<double>& coeffs, char type, double rhs) {if (i < 0 || i >= constraintCount || coeffs.size() != varCount) {cerr << "添加约束失败：参数无效！" << endl;return;}A[i] = coeffs;constraintType[i] = type;b[i] = rhs;// 确保约束右边项非负（预处理）if (b[i] < -1e-9) {b[i] *= -1.0;for (int j = 0; j < varCount; ++j) {A[i][j] *= -1.0;}// 翻转约束类型if (type == '<') constraintType[i] = '>';else if (type == '>') constraintType[i] = '<';// '='类型不受影响}}// 生成对偶问题LPModel generateDual() {// 对偶问题的变量数 = 原始问题的约束数// 对偶问题的约束数 = 原始问题的变量数int dualVarCount = constraintCount;int dualConsCount = varCount;// 原始最大化 → 对偶最小化；原始最小化 → 对偶最大化bool dualIsMaximize = !isMaximize;LPModel dualModel(dualVarCount, dualConsCount, dualIsMaximize);// 1. 对偶问题的目标函数系数 = 原始问题的约束右边项bvector<double> dualObjCoeffs = b;dualModel.setObjective(dualObjCoeffs);// 2. 对偶问题的约束矩阵 = 原始问题约束矩阵的转置A^Tvector<vector<double>> dualA(dualConsCount, vector<double>(dualVarCount, 0.0));for (int i = 0; i < dualConsCount; ++i) {      // 对偶约束i对应原始变量ifor (int j = 0; j < dualVarCount; ++j) {   // 对偶变量j对应原始约束jdualA[i][j] = A[j][i];}}// 3. 确定对偶问题的约束类型与右边项for (int i = 0; i < dualConsCount; ++i) {char dualType;double dualRhs = c[i];  // 对偶约束右边项 = 原始目标函数系数c[i]// 根据原始问题类型和变量类型确定对偶约束类型if (isMaximize) {// 原始问题为最大化时：// - 原始变量为非负（默认）→ 对偶约束为≥（'>'）// - 原始变量为自由变量 → 对偶约束为=if (varIsFree[i]) {dualType = '=';  // 自由变量对应等式约束} else {dualType = '>';  // 非负变量对应≥约束}} else {// 原始问题为最小化时：// - 原始变量为非负（默认）→ 对偶约束为≤（'<'）// - 原始变量为自由变量 → 对偶约束为=if (varIsFree[i]) {dualType = '=';  // 自由变量对应等式约束} else {dualType = '<';  // 非负变量对应≤约束}}// 添加对偶约束dualModel.addConstraint(i, dualA[i], dualType, dualRhs);}// 4. 确定对偶变量的类型（是否为自由变量）for (int j = 0; j < dualVarCount; ++j) {// 原始问题为最大化时：// - 原始约束为≤（'<'）→ 对偶变量非负（默认）// - 原始约束为≥（'>'）→ 对偶变量非正（通过设置为自由变量并在求解时处理）// - 原始约束为= → 对偶变量为自由变量if (isMaximize) {if (constraintType[j] == '=') {dualModel.setFreeVariable(j);  // 等式约束对应自由变量}// 对于'>'约束，对偶变量非正，这里简化处理为自由变量else if (constraintType[j] == '>') {dualModel.setFreeVariable(j);}} else {// 原始问题为最小化时：// - 原始约束为≥（'>'）→ 对偶变量非负（默认）// - 原始约束为≤（'<'）→ 对偶变量非正// - 原始约束为= → 对偶变量为自由变量if (constraintType[j] == '=') {dualModel.setFreeVariable(j);  // 等式约束对应自由变量}// 对于'<'约束，对偶变量非正else if (constraintType[j] == '<') {dualModel.setFreeVariable(j);}}}return dualModel;}// 打印模型void printModel() {cout << "\n===== 线性规划模型 =====" << endl;cout << "类型：" << (isMaximize ? "最大化" : "最小化") << endl;// 打印目标函数cout << "目标函数：";for (int i = 0; i < varCount; ++i) {if (isZero(c[i])) continue;if (i > 0) {cout << (c[i] > 0 ? " + " : " - ");} else {if (c[i] < 0) cout << "-";}cout << fixed << setprecision(2) << fabs(c[i]) << "y" << (i + 1);}cout << endl;// 打印约束条件cout << "约束条件：" << endl;for (int i = 0; i < constraintCount; ++i) {cout << "  ";for (int j = 0; j < varCount; ++j) {if (isZero(A[i][j])) continue;if (j > 0) {cout << (A[i][j] > 0 ? " + " : " - ");} else {if (A[i][j] < 0) cout << "-";}cout << fixed << setprecision(2) << fabs(A[i][j]) << "y" << (j + 1);}cout << " " << constraintType[i] << "= " << fixed << setprecision(2) << b[i] << endl;}// 打印变量类型cout << "变量约束：" << endl;for (int i = 0; i < varCount; ++i) {if (varIsFree[i]) {cout << "  y" << (i + 1) << " 是自由变量（无符号限制）" << endl;} else {cout << "  y" << (i + 1) << " ≥ 0" << endl;}}cout << "=======================\n" << endl;}
};// 测试案例：资源分配问题的对偶生成
int main() {// 1. 构建原始问题（资源分配问题）// 原始问题：最大化 30x1 + 50x2// 约束：// 2x1 + x2 ≤ 100 （原料X限制）// x1 + 3x2 ≤ 90   （原料Y限制）// x1, x2 ≥ 0LPModel primal(2, 2, true);  // 2个变量，2个约束，最大化// 设置目标函数vector<double> obj = {30.0, 50.0};primal.setObjective(obj);// 添加约束vector<double> cons1 = {2.0, 1.0};  // 2x1 + x2 ≤ 100primal.addConstraint(0, cons1, '<', 100.0);vector<double> cons2 = {1.0, 3.0};  // x1 + 3x2 ≤ 90primal.addConstraint(1, cons2, '<', 90.0);// 打印原始问题cout << "【原始线性规划问题】" << endl;primal.printModel();// 2. 生成对偶问题LPModel dual = primal.generateDual();// 3. 打印对偶问题cout << "【对应的对偶线性规划问题】" << endl;dual.printModel();return 0;
}

http://www.lryc.cn/news/625280.html

相关文章：

  • Matplotlib数据可视化实战：Matplotlib子图布局与管理入门
  • Day10--滑动窗口与双指针--2875. 无限数组的最短子数组，76. 最小覆盖子串，632. 最小区间
  • Hugging Face 核心组件介绍
  • 【牛客刷题】岛屿数量问题：BFS与DFS解法深度解析
  • Git的初步学习
  • 系统架构设计师-操作系统-避免死锁最小资源数原理模拟题
  • git 创用操作
  • [系统架构设计师]云原生架构设计理论与实践（十四）
  • linux系统装google chrome，amd64
  • 2025年5月架构设计师综合知识真题回顾，附参考答案、解析及所涉知识点（六）
  • 应用缓存不止是Redis！——亿级流量系统架构设计系列
  • [系统架构设计师]信息系统架构设计理论与实践（十二）
  • 监督分类——最小距离分类、最大似然分类、支持向量机
  • 利用图数据库高效解决 Text2sql 任务中表结构复杂时占用过多大模型上下文的问题
  • Apache IoTDB：大数据时代时序数据库选型的技术突围与实践指南
  • 《算法导论》第 31 章 - 数论算法
  • 开源 C++ QT Widget 开发（二）基本控件应用
  • 解决 UniApp 自定义弹框被图片或 Canvas 覆盖的 Bug
  • 【datawhale组队学习】n8n TASK01
  • 软件测试覆盖率：真相与实践
  • Mysql——分库分表后id冲突解决方案（即分布式ID的生成方案）
  • Python 作用域 (scope) 与闭包 (closure)
  • Android中使用RxJava实现网络请求与缓存策略
  • 在python中等号左边的都是对象，在matlab中等号a = 3+2 a就是个变量
  • 特征工程学习笔记
  • 无人机行业“黑话”
  • vue的双向数据绑定
  • JavaSE高级-02
  • 如何使用 React 101 的 Highcharts 包装器
  • MongoDB 查询方法与高级查询表（Python版）