当前位置：首页 > news >正文

Wasserstein GAN：如何解决GANS训练崩溃，深入浅出数学原理级讲解WGAN与WGAN-GP

news 2025/8/18 17:33:51

1. 回顾原始GAN的问题

在上一节课中我们学习了GAN网络的架构与实例训练，相信大家发现了GAN网络经常会发生训练不稳定，非常容易训练失败的现象。

在讲解Wgans之前，我们先回顾一下，关于标准GANs网络：

目标函数（Minimax Game）：

生成器 G 试图生成逼真的数据欺骗判别器 D，判别器 D 试图区分真实数据和生成数据。

问题1：训练不稳定（Mode Collapse/Dropping）

判别器 D 训练得太好，导致生成器 G 的梯度消失（D(G(z)) 接近 0，log(1 - D(G(z))) 饱和，梯度接近 0）。

判别器 D 训练得不好，导致生成器 G 得不到有用的梯度信息。

生成器 G 可能只学会生成少数几种能骗过当前判别器 D 的样本（Mode Collapse），或者完全忽略某些数据模式（Mode Dropping）。

问题2：损失函数不代表生成质量

原始GAN的损失值（生成器和判别器的loss）与生成样本的实际视觉质量之间没有必然的相关性。损失下降时，图片质量可能变好也可能变差；反之亦然。这让我们很难监控训练过程、调整超参数或决定何时停止训练。

问题根源：JS散度（Jensen-Shannon Divergence）的缺陷

理论上可以证明，当判别器 D 达到最优时，原始GAN的优化目标等价于最小化生成数据分布 $p_g$ 和真实数据分布 $p_{data}$ 之间的 JS散度（JSD）：

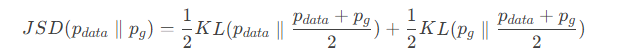
JS散度的致命缺点：当两个分布没有重叠或者重叠部分测度为零时，JSD 恒等于 log2。 这意味着：

只要 $p_g$ 和 $p_{data}$ 不重叠（在高维空间中，低维流形很容易不重叠），无论它们距离是远还是近，JSD 都是常数 log2。
梯度消失： 最优判别器 D 给出的梯度在理论上为 0（因为 JSD 的梯度在分布不重叠时为 0）。即使在实际中梯度不为零，也通常非常不可靠（方差大）。
无法提供有意义的距离度量： 无法通过 JSD 的大小来判断 $p_g$ 是否在向 $p_{data}$ 靠近。

讲完了标准GANS的缺点，我们进入Wgans学习！

2. Wasserstein 距离：一个更好的度量

WGAN 的核心贡献在于用 Wasserstein 距离（Earth-Mover Distance, EM Distance） 替代了 JS 散度作为衡量两个分布差异的度量。这个距离也称为推土机距离

直观理解 (Earth-Mover's Distance):

想象你有两堆土，一堆是分布 $p_{data}$ ，另一堆是分布 $p_g$ 。Wasserstein 距离衡量的是把 $p_g$ 这堆土“搬动”成 $p_{data}$ 这堆土所需的最小“工作量”。

“工作量”定义为：移动的土方量 × 移动的距离。

这个距离即使在两个分布没有重叠的情况下，也能敏感地反映出它们之间的远近。分布越接近，搬运土方所需的“工作量”越小。

数学定义 (1st-Wasserstein Distance):
对于两个概率分布 $p_{data}$ 和 $p_g$ 定义在空间 $\chi$ 上，它们的 1st-Wasserstein 距离定义为：

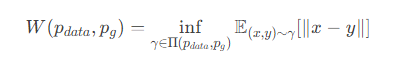
$\Pi(p_{data}, p_g)$ 表示所有以 $p_{data}$ 和 $p_g$ 为边缘分布的联合分布 $\gamma(x, y)$ 的集合。可以把 $\gamma(x, y)$ 理解为在 $p_{data}$ 中取点 $x$ 的同时在 $p_g$ 中取点 $y$ 的一个运输方案。
$\mathbb{E}_{(x, y) \sim \gamma} [| x - y |]$ 是在该运输方案下，把 $x$ 处的“质量”运到 $y$ 处的期望代价（这里代价用欧氏距离 $|x - y|$ 衡量）。
$\inf$ 表示取下确界，即寻找所有可能运输方案中期望代价最小的那个方案。这个最小的期望代价就是 Wasserstein 距离。

3. WGAN：用Wasserstein距离重构GAN

Arjovsky 等人在论文《Wasserstein GAN》中提出，最小化 $p_g$ 和 $p_{data}$ 之间的 Wasserstein 距离 $W(p_{data}, p_g)$ 是一个比最小化 JSD 更好的目标。优点在于：

处处连续且（几乎）处处可导： 即使在分布不重叠时，也能提供有意义的梯度。
损失值反映生成质量： $W(p_{data}, p_g)$ 的值越小，通常意味着 $p_g$ 越接近 $p_{data}$ ，生成质量越好。这解决了监控问题。

关键挑战： 直接计算 $W(p_{data}, p_g) = \inf_{\gamma \in \Pi} \mathbb{E}[|x - y|]$ 是极其困难的（涉及到在所有联合分布上求下确界）。

突破性转化：Kantorovich-Rubinstein Duality (对偶性)

数学上的 Kantorovich-Rubinstein 对偶定理提供了计算 Wasserstein 距离的另一种等价形式：

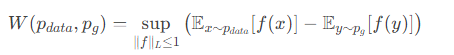
这个公式意义重大：

$\sup$ 表示取上确界。
$f: \chi \to \mathbb{R}$ 是一个满足 1-Lipschitz 连续性 约束的实值函数，即 $|f|_L \leq 1$ 。这意味着函数 $f$ 的输出变化不能快于输入变化：

这个公式的含义是：Wasserstein 距离等于在满足 1-Lipschitz 约束 的所有函数 $f$ 中，找到使得 $\mathbb{E}{x \sim p{data}}[f(x)] - \mathbb{E}_{y \sim p_g}[f(y)]$ 最大的那个函数 $f$ 时得到的最大值。

4. WGAN 算法构建

Kantorovich-Rubinstein 对偶性为构建 WGAN 提供了清晰的路径：

判别器变评论家 (Critic)： 用函数 $f_w$ (通常是一个神经网络，参数为 $w$ ) 来逼近对偶问题中要求的函数 $f$ 。这个 $f_w$ 不再像原始GAN的判别器 D 那样输出一个概率（0到1之间），而是输出一个实数分数 (Critic Score)。这个分数可以理解为样本“真实程度”的评分，没有固定的范围。
Lipschitz 约束： 为了满足 $|f_w|_L \leq 1$ ，必须对 $f_w$ 施加约束。最初的 WGAN 论文采用了简单但有效的 Weight Clipping (权重裁剪)：在每次梯度更新后，将 $f_w$ 的参数 $w$ 强行裁剪到一个很小的区间 $[-c, c]$ （例如 $c=0.01$ ）。直观上，限制权重的绝对值大小就限制了函数 $f_w$ 梯度的最大值，从而（近似）满足 Lipschitz 约束。
损失函数： 基于对偶形式，WGAN 的损失函数变得非常简单：

评论家 (Critic) $f_w$ 的损失 (最大化)：

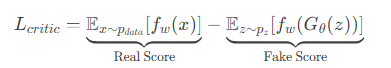
评论家 $f_w$ 的目标是尽可能拉大真实样本分数与生成样本分数的差距。

生成器 (Generator) $G_\theta$ 的损失 (最小化)：

生成器 $G_\theta$ 的目标是让生成样本在评论家 $f_w$ 那里获得尽可能高的分数（因为评论家分数高代表“真实”）。

4.训练流程：

初始化评论家 $f_w$ 和生成器 $G_\theta$ 的参数。
在每个训练迭代中：
1. 训练评论家 $f_w$ ：
  - 多次（例如 5 次）更新评论家（原始论文建议 n_critic=5）。
  - 采样一批真实数据 $x \sim p_{data}$ 。
  - 采样一批噪声 $z \sim p_z$ ，生成假数据 $\tilde{x} = G_\theta(z)$ 。
  - 计算评论家损失 $L_{critic} = \mathbb{E}[f_w(x)] - \mathbb{E}[f_w(\tilde{x})]$ 。
  - 通过梯度上升（最大化 $L_{critic}$ ）更新 $f_w$ 的参数 $w$ 。
  - 关键步骤： 将 $f_w$ 的所有参数 $w$ 裁剪到 $[-c, c]$ 。
2. 训练生成器 $G_\theta$ ：
  - 采样一批噪声 $z \sim p_z$ 。
  - 计算生成器损失 $L_{generator} = -\mathbb{E}[f_w(G_\theta(z))]$ 。
  - 通过梯度下降（最小化 $L_{generator}$ ）更新 $G_\theta$ 的参数 $\theta$ 。
评论家 $f_w$ 的目标是最大化真实与假样本的分数差（ $L_{critic}$ ），生成器 $G_\theta$ 的目标是最大化假样本的分数（最小化负分数 $L_{generator}$ ）。这是一个极小极大博弈，但目标函数是 Wasserstein 距离的对偶形式。

5. WGAN 的优势

显著提升训练稳定性： Wasserstein 距离提供的梯度在理论上是更可靠的，大大减少了模式崩溃（Mode Collapse）的发生。
有意义的损失度量： 评论家损失 $L_{critic}$ 的值（或其绝对值）可以作为生成器性能的指示器。这个值在训练过程中持续下降，通常意味着生成质量在提升。这是调试模型、选择超参数和决定何时停止训练的无价工具。
改进的生成质量 (尤其在某些数据集上)： 虽然不一定在所有情况下都绝对优于后续改进（如 WGAN-GP），但 WGAN 通常能生成更清晰、更多样化的样本。

6. 改进：WGAN-GP (Gradient Penalty)

原始的 WGAN 使用权重裁剪 (Weight Clipping) 来强制 Lipschitz 约束，但存在一些问题：

容量限制 (Capacity Underuse)： 裁剪可能迫使神经网络使用更简单的函数（饱和非线性），降低了其表达能力。
梯度爆炸/消失： 裁剪阈值 c 是一个敏感的超参数。c 太小会导致梯度消失，c 太大会导致梯度爆炸或不满足约束。
不精确的约束： 权重裁剪只能保证 $f_w$ 是 K-Lipschitz 的（ $K$ 取决于网络结构），而不是精确的 1-Lipschitz。

WGAN-GP (Gulrajani et al.) 提出了一种更有效的方法来强制 Lipschitz 约束：梯度惩罚 (Gradient Penalty)。

核心公式

1. Critic（判别器）损失函数

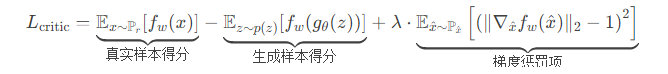
2. 随机插值点 𝑥^x^ 的构造

3. 梯度惩罚项详解

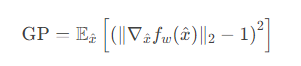
4. 生成器损失函数

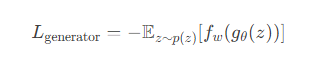
生成器目标是最大化生成样本的 Critic 得分（即最小化负得分）

关键改进：梯度惩罚 vs 权重裁剪

方法	WGAN	WGAN-GP
Lipschitz 约束	权重裁剪（Weight Clipping）	梯度惩罚（Gradient Penalty）
问题	梯度消失/爆炸，训练不稳定	稳定训练，高质量生成
计算	硬性截断权重值	在插值点 𝑥^ 处惩罚梯度范数

梯度惩罚的数学原理

Wasserstein 距离要求 Critic 满足 1-Lipschitz 连续性：

训练过程

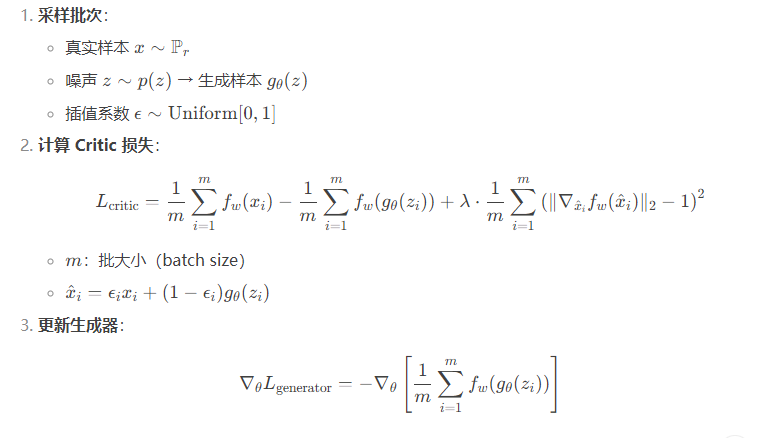
7. 总结

WGAN 的核心： 用 Wasserstein 距离 替代 JS 散度 作为衡量生成分布与真实分布差异的度量。
Wasserstein 距离的优势： 即使分布不重叠也能提供有意义的距离和可靠的梯度。
关键转化： 利用 Kantorovich-Rubinstein 对偶性，将难以计算的 Wasserstein 距离下确界问题转化为一个在 Lipschitz 函数族 上求上确界的问题。
实现：
- 用一个输出实数的评论家 (Critic) 网络 $f_w$ 逼近 Lipschitz 函数。
- 损失函数极其简单： 评论家损失 = $\mathbb{E}[f_w(real)] - \mathbb{E}[f_w(fake)]$ ，生成器损失 = $-\mathbb{E}[f_w(fake)]$ 。
- 必须强制 $f_w$ 满足 1-Lipschitz 约束：
  - WGAN (原始)： 权重裁剪 (Weight Clipping) -> 简单但效果有限。
  - WGAN-GP (改进)： 梯度惩罚 (Gradient Penalty) -> 更优的标准方法。
主要优势：
- 训练更稳定，减少模式崩溃。
- 损失值 ( $L_{critic}$ ) 成为生成质量的可靠指示器，解决了训练监控难题。