照相机标定-动手学计算机视觉16

简介

拍摄图像作为捕捉和记录这个世界的一个主要手段，在我们生活的三维世界中扮演着不可或缺的角色。图像是由照相机成像函数将真实世界的场景投影到二维平面上的视觉记录，为我们提供了观察和理解世界的一个窗口。然而真实的世界是三维的，而记录下来的图像是二维的，且图像的分辨率有限，因此这一转换过程不可避免地伴随着信息的损失。尽管如此，我们仍然希望能够通过图像重建出其中描述的场景。为了向这一目标迈进，我们必须首先深入了解照相机成像函数。因为只有完全掌握了照相机将三维世界投影到二维图像的原理，我们才有可能逆向这一过程，实现从图像到场景的还原，即从二维信息恢复三维信息。在本章中，我们将先介绍照相机成像的基本原理，即照相机如何确立真实三维空间中一点与其在二维图像上投影点之间的映射关系，然后介绍如何通过照相机标定(camera calibration)来计算照相机的成像过程中的参数。

照相机成像原理

尽管现实世界中的照相机光学系统极其复杂，但是照相机成像函数f的核心原理却与简化模型无太大差异。为了便于计算和阐述，我们采用简化的针孔照相机模型和透镜照相机模型来近似实际照相机的工作原理。针孔照相机模型，作为一种基础且高效的理论模型，阐释了光通过一个小孔并在另一侧的光屏（成像平面）上形成图像的过程。虽然理论上，小孔成像能够产生清晰的图像，但是由于小孔只允许极少的光线进入，因此成像亮度很低，这不仅限制了在光线不足的情况下小孔成像的使用，还要求较长的曝光时间以获得清晰的图像。而透镜照相机模型采用凸透镜来代替针孔模型中的小孔进行成像，更加贴近我们实际使用的照相机。需要注意的是，透镜的制造和组装过程可能引入某些偏差，这些偏差将导致光线并不完全按照预期的路径传播，从而引起图像畸变(distortion)。通过照相机标定，我们可以建模这些畸变，并有效地纠正它们。

照相机成像的基本原理可以概括为光线通过镜头聚焦，在感光介质上形成倒立实像的过程，结合了光学和化学（或电子）技术。以下是分步说明：

1. 光线进入镜头

• 当按下快门时，相机镜头会打开，外界光线通过镜头组（由凸透镜、凹透镜等组成）进入相机。
• 镜头的作用：通过调节透镜组合（对焦）将散射的光线汇聚到一点，形成清晰的像。现代镜头还能矫正畸变、色差等光学问题。

2. 聚焦成像

• 光线通过镜头后，会在相机内部的像平面（传统相机是胶片，数码相机是图像传感器）上形成倒立的实像。
• 小孔成像类比：这与初中物理中的“小孔成像”原理类似，但镜头通过透镜组大幅提升进光量和成像质量。
• 对焦调节：通过移动透镜位置，使不同距离的物体都能在像平面上清晰成像（如手动/自动对焦）。

3. 感光介质记录图像

• 传统胶片相机：
  胶片上的卤化银颗粒发生化学反应，记录光线的强弱和颜色，经显影后形成负片。
• 数码相机：
  图像传感器（CMOS或CCD）将光信号转换为电信号。每个像素点记录光的强度（通过光电二极管），再通过处理器转换为数字图像。

4. 附加关键部件

• 光圈：控制进光量的开口大小（如f/2.8大光圈适合弱光环境）。
• 快门：控制曝光时间（如1/1000秒冻结高速运动）。
• ISO：调节感光度（数码相机通过放大信号模拟高感光）。

5. 最终图像处理

• 数码相机会对原始信号进行降噪、色彩校正等处理，输出JPEG、RAW等格式文件。

一句话总结

相机本质是“复制”人眼：镜头如晶状体聚焦，光圈如瞳孔调节进光，感光元件如视网膜记录信息，最终形成图像。

关于具体细节这里不多加概述。

了解各种坐标系

世界坐标系：三维坐标系，用于描述空间点在真实世界的绝对位置，任何空间点在世界坐标系中有唯一的坐标。由于照相机本身存在于三维空间，因此我们使用世界坐标系记录照相机的空间坐标。世界坐标系的单位一般是m。也就是在世界里的哪个地点拍的照片的坐标

照相机坐标系：三维坐标系，为了方便描述在照相机视角下空间点的位置而定义的坐标系。照相机坐标系是以照相机的光心为原点的坐标系，可由世界坐标系通过平移和旋转得到。照相机坐标系的单位一般是也m。

图像坐标系：二维坐标系，以成像平面左上角为原点，一般用(u,v)表示坐标。图像坐标系的单位是像素。

前面提到小孔成像的进光量不足，因此我们通常使用透镜来代替小孔进行成像。然而，透镜的制造和组装过程可能引入某些偏差，这些偏差将导致光线并不完全按照预期的路径传播，从而引起图像畸变。

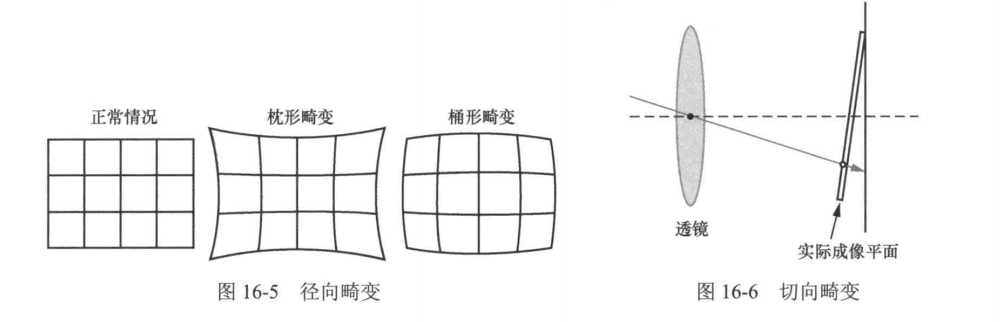
径向畸变

由透镜设计及光学特性导致，表现为光线偏离理想聚焦路径。中心区域畸变较小，边缘畸变显著，分为两种形式：

• 桶形畸变：图像边缘向外膨胀。
• 枕形畸变：图像边缘向中心凹陷。
  畸变程度随与透镜中心距离增加而增强。

切向畸变

因透镜与成像平面不平行（制造或装配误差）引起。光线以倾斜角度抵达成像平面，导致图像边缘拉伸或压缩，表现为直线弯曲。

畸变成因对比

• 径向畸变：透镜球面像差导致光线聚焦偏移。
• 切向畸变：透镜与成像平面夹角破坏光线垂直入射条件。

照相机标定的实现原理

照相机标定是通过已知的三维空间点及其对应的二维图像投影点，反向求解照相机内外参数和畸变参数的过程。其核心思想是通过优化重投影误差（即理论投影点与实际观测点的差异）来估计参数。

标定板的作用

标定板提供了一系列已知几何尺寸和位置的三维空间点（如棋盘格角点），其高对比度图案便于图像处理算法精确提取对应二维投影点。常见的棋盘格标定板通过黑白方格的交点作为特征点，这些交点的物理坐标和图像坐标构成标定的输入数据。

标定流程的关键步骤

数据采集
使用标定板拍摄多张不同角度和位置的图像，确保覆盖成像平面的各个区域。每张图像需提取棋盘格角点的像素坐标，并与已知的物理坐标配对。

参数初始化
为内参（焦距、主点坐标等）和外参（旋转矩阵、平移向量）提供初始估计值。内参可通过图像分辨率和假设的近似焦距初始化，外参可通过棋盘格平面与相机坐标系的相对位置估算。

非线性优化
构建重投影误差目标函数，通过优化算法（如Levenberg-Marquardt）迭代调整参数，最小化所有观测点的重投影误差总和。畸变参数（径向、切向畸变）通常在此阶段联合优化。

验证与评估
计算重投影误差的均值和标准差，评估标定结果的精度。若误差较大，需检查数据质量（如角点提取准确性）或重新采集更多样化的图像。

数学表达

设三维点 通过投影模型映射到图像点，其重投影误差为：
其中 为投影函数， 为内参矩阵， 为畸变参数， 为外参。优化目标是最小化所有点的 e 之和。

注意事项

• 标定板需平整，图案尺寸需精确已知。
• 图像数量建议不少于10张，覆盖不同视角以提升鲁棒性。
• 强光照或反光可能影响角点检测，需控制环境光线。

通过上述流程，可高精度求解相机参数，为后续三维重建、视觉测量等任务提供基础。

代码实现

接下来，我们来学习照相机标定的代码实现。为了方便理解，我们不考虑照相机畸变的影响。整个流程包括从标定板图像中提取角点，计算单应性矩阵，求解内参矩阵，求解外参矩阵，最后通过重投影误差来评估标定的准确性。这里我们采用OpenCV样例中的标定图像作为样例，有条件的同学也可以自己打印或者购买标定板进行拍照获取标定板图像。

在这里我们将介绍一下OpenCV标定算法的标定流程：

（1）：由于镜头畸变的影响比较小，首先假定照相机是理想无畸变的，根据角点的二维坐标与三维坐标的对应关系来计算初始的照相机内参；

（2）：求解照相机外参；

（3）：应用最小二乘求解实际的畸变系数；

（4）：根据求解的内外参对空间点进行重投影，应用全局优化算法来最小化重投影和原投影点之间的误差。

In [4]:

# 首先clone对应仓库
! git clone https://github.com/boyu-ai/Hands-on-CV.git

Cloning into 'Hands-on-CV'...
remote: Enumerating objects: 9, done.
remote: Counting objects: 100% (9/9), done.
remote: Compressing objects: 100% (4/4), done.
remote: Total 9 (delta 1), reused 5 (delta 0), pack-reused 0
Receiving objects: 100% (9/9), done.
Resolving deltas: 100% (1/1), done.

In [1]:

import cv2
import glob
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline# 首先获取图像路径
image_dirs = sorted(glob.glob("./Hands-on-CV/第13章 照相机标定/left*.jpg"), key=lambda x: int(x.split("/")[-1].split(".")[0][4:]))# 可视化4张棋盘格图像
plt.figure()
for i in range(4):plt.subplot(2, 2, i+1)img = cv2.imread(image_dirs[i], 0)plt.imshow(img, cmap="gray")plt.axis("off")

从上图可以看到在标定板上的角点，我们可以通过角点检测算法来获取这些角点的坐标。在OpenCV中提供了一个函数 cv2.findChessboardCorners() 来帮助我们检测棋盘格角点。

In [54]:

def detect_corner(image_dirs):"""检测图像中的角点并返回，同时可视化角点检测效果。"""# 根据标定板决定用来标定的角点的个数，这里以(7, 6)为例num_corner = (7, 6)# 创建一个列表来保存每张图像中角点的三维坐标objpoints = []# 创建一个列表来保存每张图像中角点的二维坐标imgpoints = []#定义三维坐标:[row, co1, z]objp = np.zeros((6*7,3), np.float32)objp[:,:2] = np.mgrid[0:num_corner[0], \0:num_corner[1]].T.reshape(-1,2)# 遍历所有图像，找到角点for fname in image_dirs:img = cv2.imread(fname)# 转化成灰度图，方便角点检测gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 使用角点检测寻找角点坐标，如果找到ret返回True# 左上角为坐标原点ret, corners = cv2.findChessboardCorners(gray, num_corner, None)# 根据ret的状态来记录角点if ret == True:objpoints.append(objp[:, :2])imgpoints.append(corners.reshape(-1, 2))# 使用OpenCV自带的绘图可视化角点检测效果，从红色开始绘制，紫色结束cv2.drawChessboardCorners(img, (7,6), corners, ret)plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))plt.show()return objpoints, imgpoints, gray# 调用detect_corner函数检测每张图像的角点
objpoints, imgpoints, gray = detect_corner(image_dirs)

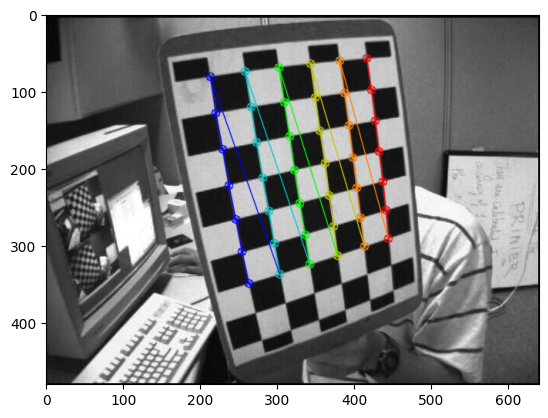
到这里我们就得到了图像上角点的图像坐标以及其对应的世界坐标系中的坐标，接下来我们就可以利用这些坐标之间的对应关系求解单应性矩阵 $\boldsymbol{H}$。

In [3]:

def normalizing_input_data(coor_data):# 计算坐标数据的平均值x_avg = np.mean(coor_data[:, 0])y_avg = np.mean(coor_data[:, 1])# 计算坐标数据的标准差，并用它来计算尺度因子，使得归一化后的坐标的标准差为sqrt(2)sx = np.sqrt(2) / np.std(coor_data[:, 0])sy = np.sqrt(2) / np.std(coor_data[:, 1])# 构造归一化矩阵，用于将坐标归一化，使均值为0，标准差为sqrt(2)norm_matrix = np.array([[sx, 0, -sx * x_avg],[0, sy, -sy * y_avg],[0, 0, 1]])return norm_matrixdef compute_homography(pic_coor, real_coor):"""计算单应性矩阵H。参数：- pic_coor: 图像坐标系坐标。- real_coor: 世界坐标系坐标。返回：- H: 单应性矩阵。"""pic_norm_mat = normalizing_input_data(pic_coor)real_norm_mat = normalizing_input_data(real_coor)A = []  # 构建用于求解H的线性方程组for i in range(len(pic_coor)):# 将当前的图像坐标系坐标和世界坐标系坐标转换为齐次坐标single_pic_coor = np.array([pic_coor[i][0], pic_coor[i][1], 1])single_real_coor = np.array([real_coor[i][0], real_coor[i][1], 1])# 对坐标进行归一化处理pic_norm = np.dot(pic_norm_mat, single_pic_coor)real_norm = np.dot(real_norm_mat, single_real_coor)# 根据归一化后的坐标构造矩阵A的行# 这部分实现了将单应性矩阵H的约束条件转换为线性方程的过程A.append(np.array([-real_norm.item(0), -real_norm.item(1), -1, 0, 0, 0,pic_norm.item(0) * real_norm.item(0), pic_norm.item(0) * real_norm.item(1),pic_norm.item(0)]))A.append(np.array([0, 0, 0, -real_norm.item(0), -real_norm.item(1), -1,pic_norm.item(1) * real_norm.item(0), pic_norm.item(1) * real_norm.item(1),pic_norm.item(1)]))# 使用奇异值分解(SVD)求解Mh=0中的h，即单应性矩阵H的向量化形式U, S, VT = np.linalg.svd((np.array(A, dtype='float')).reshape((-1, 9)))H = VT[-1].reshape((3, 3))  # 最小奇异值对应的奇异向量重塑为3x3矩阵# 对H进行反归一化处理H = np.dot(np.dot(np.linalg.inv(pic_norm_mat), H), real_norm_mat)H = H / H[-1, -1]  # 归一化，确保H的最后一个元素为1return HH_list = []
for i in range(len(objpoints)):H = compute_homography(imgpoints[i], objpoints[i])H_list.append(H)if i < 3:print("第{}张图像的单应性矩阵为：\n{}".format(i+1, H))

第1张图像的单应性矩阵为：
[[-2.90500492e+01 -2.05911540e+00  4.76529133e+02][ 2.28048296e+00 -3.63192023e+01  2.64694023e+02][ 1.49422654e-02 -5.06829993e-03  1.00000000e+00]]
第2张图像的单应性矩阵为：
[[-1.28830042e+01  3.91039199e+01  2.53736256e+02][-4.27973766e+01  7.39439498e+00  3.09778969e+02][-4.92899678e-02 -3.79194108e-03  1.00000000e+00]]
第3张图像的单应性矩阵为：
[[-4.25026982e+01  2.84366906e+01  5.00044815e+02][-1.26971800e+01 -4.04613414e+01  3.75934812e+02][ 1.57645215e-02  2.74643346e-02  1.00000000e+00]]

在得到了每张标定板图像对应的 之后，我们首先需要从每个单应性矩阵$\boldsymbol{H}$中提取出用于解矩阵 $\boldsymbol B$ 的约束方程。然后再通过SVD分解求解出 $\boldsymbol B$，最后通过楚列斯基分解求解出照相机的内参矩阵 $\boldsymbol K$。

In [12]:

def compute_B_matrix(H_list):"""从单应性矩阵H列表中计算B矩阵。参数：- H_list: 单应性矩阵H的列表。返回：- B: B矩阵。"""V = []for H in H_list:# 分解H矩阵以获得其列向量h1, h2, _ = H[:,0], H[:,1], H[:,2]# 根据旋转矩阵的正交性质构造V矩阵的行# v_ij 是构造方程 hi^T * B * hj = 0 的向量形式# 由于 h = K * r，我们可以用 h 来代替 r# 第一个方程来自于 r1^T * r2 = 0 -> (h1^T * B * h2 = 0)v12 = np.array([h1[0]*h2[0], h1[0]*h2[1] + h1[1]*h2[0], h1[1]*h2[1], h1[2]*h2[0] + h1[0]*h2[2], h1[2]*h2[1] + h1[1]*h2[2], h1[2]*h2[2]])# 第二个方程来自于 r1^T * r1 = r2^T * r2 -> # ((h1^T * B * h1) - (h2^T * B * h2) = 0)v11_v22 = np.array([h1[0]**2 - h2[0]**2, 2*(h1[0]*h1[1] - h2[0]*h2[1]), h1[1]**2 - h2[1]**2, 2*(h1[2]*h1[0] - h2[2]*h2[0]), 2*(h1[2]*h1[1] - h2[2]*h2[1]), h1[2]**2 - h2[2]**2])# 将这两个方程添加到V矩阵中V.append(v12)V.append(v11_v22)V = np.array(V)# 使用SVD求解b，其中b是B矩阵的六个未知数的向量形式U, S, Vt = np.linalg.svd(V)b = Vt[-1]  # 与最小奇异值对应的奇异向量# 根据b重构B矩阵B = np.array([[b[0], b[1], b[3]],[b[1], b[2], b[4]],[b[3], b[4], b[5]]])return BB = compute_B_matrix(H_list)
print("B矩阵为：\n{}".format(B))

B矩阵为：
[[ 2.16451749e-06  7.58169969e-09 -7.67824576e-04][ 7.58169969e-09  2.15556058e-06 -4.90907403e-04][-7.67824576e-04 -4.90907403e-04  9.99999585e-01]]

接下来我们使用楚列斯基分解求解出照相机的内参矩阵 $\boldsymbol K$。

In [17]:

def cholesky_solve(B):"""利用楚列斯基分解求解 K 矩阵。"""# 检查 B 是否为对称矩阵if not np.allclose(B, B.T):raise ValueError("B is not a symmetric matrix")# 进行楚列斯基分解L = np.linalg.cholesky(B)# L是下三角矩阵，而我们的K是上三角矩阵K = np.linalg.inv(L.T)# K矩阵的最后一个元素为1K = K / K[-1, -1]return K# 直接求解
K = cholesky_solve(B)
print("K矩阵为：\n{}".format(K))

K矩阵为：
[[533.92350191  -1.87407784 353.93909352][  0.         535.03494272 226.49511563][  0.           0.           1.        ]]

接下来我们再从单应性矩阵计算照相机的外参矩阵 $[\boldsymbol{R} | \boldsymbol{t}]$。

In [24]:

def get_extrinsics_param(H, intrinsics_param):"""从单应性矩阵H和内参矩阵K中计算外参矩阵R和平移向量t，并确保R的行列式为1。参数：- H: 单应性矩阵H列表。- intrinsics_param: 内参矩阵K。返回：- extrinsics_param: 包含外参矩阵R和平移向量t的列表。"""extrinsics_param = []inv_intrinsics_param = np.linalg.inv(intrinsics_param)for i in range(len(H)):h0 = (H[i].reshape(3, 3))[:, 0]h1 = (H[i].reshape(3, 3))[:, 1]h2 = (H[i].reshape(3, 3))[:, 2]scale_factor = 1 / np.linalg.norm(np.dot(inv_intrinsics_param, h0))r0 = scale_factor * np.dot(inv_intrinsics_param, h0)r1 = scale_factor * np.dot(inv_intrinsics_param, h1)t = scale_factor * np.dot(inv_intrinsics_param, h2)r2 = np.cross(r0, r1)# 构成近似旋转矩阵R_approx = np.array([r0, r1, r2]).transpose()# 使用SVD来修正R，确保其符合旋转矩阵的性质U, _, Vt = np.linalg.svd(R_approx)R_corrected = np.dot(U, Vt)# 确保R的行列式为1if np.linalg.det(R_corrected) < 0:U[:, -1] *= -1  # 调整U的最后一列R_corrected = np.dot(U, Vt)  # 重新计算Rextrinsics = np.column_stack((R_corrected, t))extrinsics_param.append(extrinsics)return extrinsics_paramextrinsics_param = get_extrinsics_param(H_list, K)
for i in range(len(extrinsics_param)):print("第{}张图像的外参矩阵为：\n{}".format(i+1, extrinsics_param[i]))if i == 2:break

第1张图像的外参矩阵为：
[[-9.73670749e-01  9.02344992e-04  2.27957142e-01  3.47913167e+00][-1.90344917e-02 -9.96821819e-01 -7.73559911e-02  1.08066170e+00][ 2.27162851e-01 -7.96583141e-02  9.70593423e-01  1.51363433e+01]]
第2张图像的外参矩阵为：
[[ 0.11529592  0.97966689  0.16419391 -2.41686208][-0.76215049  0.19325491 -0.61788281  2.01046147][-0.63705061 -0.0539011   0.7689351  12.91567438]]
第3张图像的外参矩阵为：
[[-0.9339432   0.35280444  0.05726373  2.84741705][-0.31749332 -0.89247809  0.32043853  2.89596682][ 0.16415876  0.28109053  0.94553689 10.36835246]]

接下来我们可以将空间中点根据我们计算得到的内参和外参投影到图像平面上，然后计算重投影误差来判断我们标定的准确程度。

In [37]:

def reproject_error(K, extrinsic, pixel_coor, real_coor):"""计算重投影误差。参数：- K: 内参矩阵。- extrinsic: 外参矩阵。- pixel_coor: 图像坐标系坐标。- real_coor: 世界坐标系坐标。返回：- error: 重投影误差。"""# 计算投影矩阵P = np.dot(K, extrinsic)# 将世界坐标系坐标转换为齐次坐标real_coor = np.column_stack((real_coor, np.zeros(len(real_coor)), np.ones(len(real_coor))))# 计算重投影坐标reprojected_coor = np.dot(P, real_coor.T).Treprojected_coor = reprojected_coor[:, :2] / reprojected_coor[:, 2:3]# 计算重投影误差error = np.linalg.norm(reprojected_coor - pixel_coor, axis=1)return error.mean()# 将内外参矩阵都转化为齐次坐标
K_homo = np.column_stack((K, np.zeros(3)))
K_homo = np.row_stack((K_homo, [0, 0, 0, 1]))# 计算所有图像重投影误差的均值
mean_error = 0
for j in range(len(imgpoints)):extrinsic_homo = np.row_stack((extrinsics_param[j], [0, 0, 0, 1]))# 计算每一张图像的重投影误差error = reproject_error(K_homo, extrinsic_homo, imgpoints[j], objpoints[j])mean_error += error# 得到平均重投影误差
mean_error /= len(imgpoints) 
print("平均重投影误差为: {}".format(mean_error))

平均重投影误差为: 2.2527822694246837

到这里，我们就完成了基础的照相机标定流程。从重投影误差来看，我们计算出来的照相机参数还是比较精确的，平均误差为 2.25 个像素。在实际应用过程中，我们往往直接使用 OpenCV 的标定函数来实现照相机标定：

In [63]:

# 转换成OpenCV需要的格式
objpoints_cv = [np.hstack((i, np.zeros((i.shape[0], 1)))).astype(np.float32) for i in objpoints]
imgpoints_cv = [i[:,None,:] for i in imgpoints]# 使用OpenCV的标定函数来标定照相机
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints_cv, imgpoints_cv, gray.shape[::-1], None, None)print("照相机内参:")
# 照相机内参，输出格式为 [[fx,0,cx],[0,fy,cy],[0,0,1]]
print(mtx,"\n")print("畸变参数:")
# k1,k2,p1,p2,k3
print(dist)

照相机内参:
[[530.16217137   0.         341.48703364][  0.         530.21111757 230.10277488][  0.           0.           1.        ]] 畸变参数:
[[-3.60236613e-01  8.54966618e-01  5.79031024e-04 -4.97455055e-04-2.16444973e+00]]

In [62]:

# 初始化误差
mean_error = 0
for i in range(len(objpoints_cv)):# 使用内外参和畸变参数对点进行重投影imgpoints2, _ = cv2.projectPoints(objpoints_cv[i], rvecs[i], tvecs[i], mtx, dist)# 计算重投影点与原始点的误差，使用欧几里得距离进行衡量error = cv2.norm(imgpoints_cv[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)# 累加误差mean_error += error# 得到平均每个点偏移像素的二范数
mean_error /= len(objpoints_cv) 
print("OpenCV得到的平均重投影误差为: {}".format(mean_error))

OpenCV得到的平均重投影误差为: 0.062162126761103303

可以发现我们的简易算法和OpenCV得到的标定结果大体上是一致的，只是精度上有一些差异，主要原因是畸变参数的影响。

小结

本章主要介绍了照相机成像的基本原理，以及照相机模型中重要的参数：内外参数和畸变参数。我们还学习了如何使用标定板对照相机进行标定，并通过代码实现了照相机的标定。经过标定的照相机，犹如一座连接三维世界与二维图像平面的桥梁。它让我们能够通过图像来反向推算三维空间的信息，为后续的计算机视觉应用提供重要的基础。下一节，我们将学习光流与运动场，探究空间运动与图像像素变化之间的关系。