【架构师从入门到进阶】第五章：DNSCDN网关优化思路——第十一节：网关安全-对称与非对称加密

对称加密

什么是对称加密呢？

指的是加密和解密使用的密钥是同一个密钥。

举个例子。

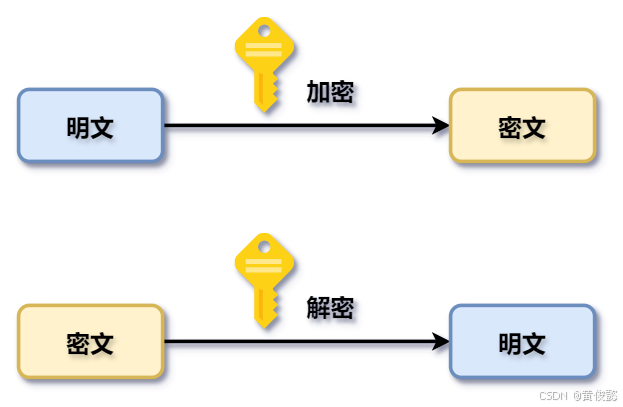
这是明文，然后我要把它加成一个密文，然后我们用的密钥是a，那么从密文要把它解密成明文用的密钥还是a，这个叫做对称加密。

这个应用的场合，比如说我们的cookie，我们的cookie就是用的这个对称加密。

• 优点：对称加密的优点是算法简单，加解密的效率比较高，系统的开销比较小，适合对大量数据的加密。
• 缺点：缺点就是，大家可以看到了它的加密和解密使用的是同一个密钥，远程通讯的情况下，如何安全的去传输这个密钥是一个难题，如果密钥丢了，那么所有的加密信息就没有秘密可言。

常用的对称加密的算法有DES算法，对称加密是一种非常传统的加密算法，但是它也是一种很常用的加密方法，适合于绝大多数需要加密的场合。

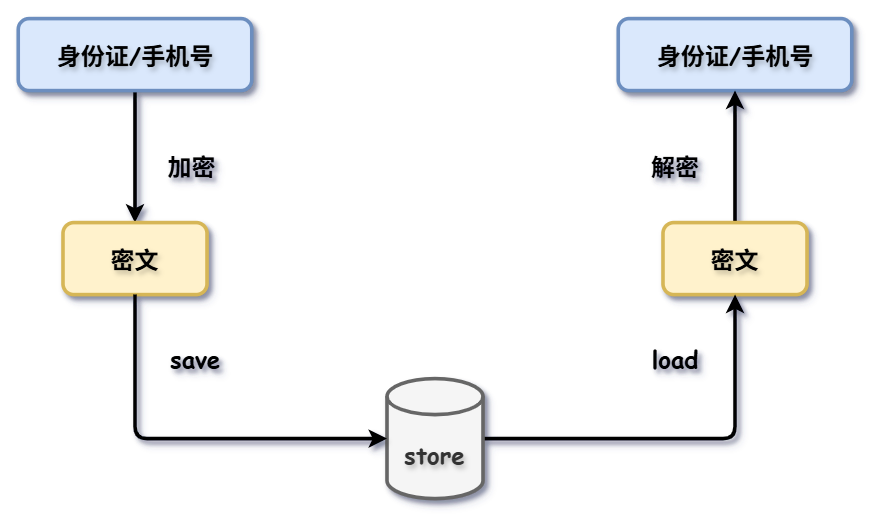
比如说，在网站的安全性方面，用户有很多信息在我们的数据库里需要存储，但是他又需要在我们的系统中进行查看。比如说身份证的信息，还有就是手机号的信息，存储到数据库中，它是一个密文，但是当用户使用我们的系统去查看他的身份证信息的时候，必须让用户看到的是一个明文。那么这种情况下加密是我们做，解密也是我们做，所以这个时候就用到了对称加密这么一种算法。

非对称加密

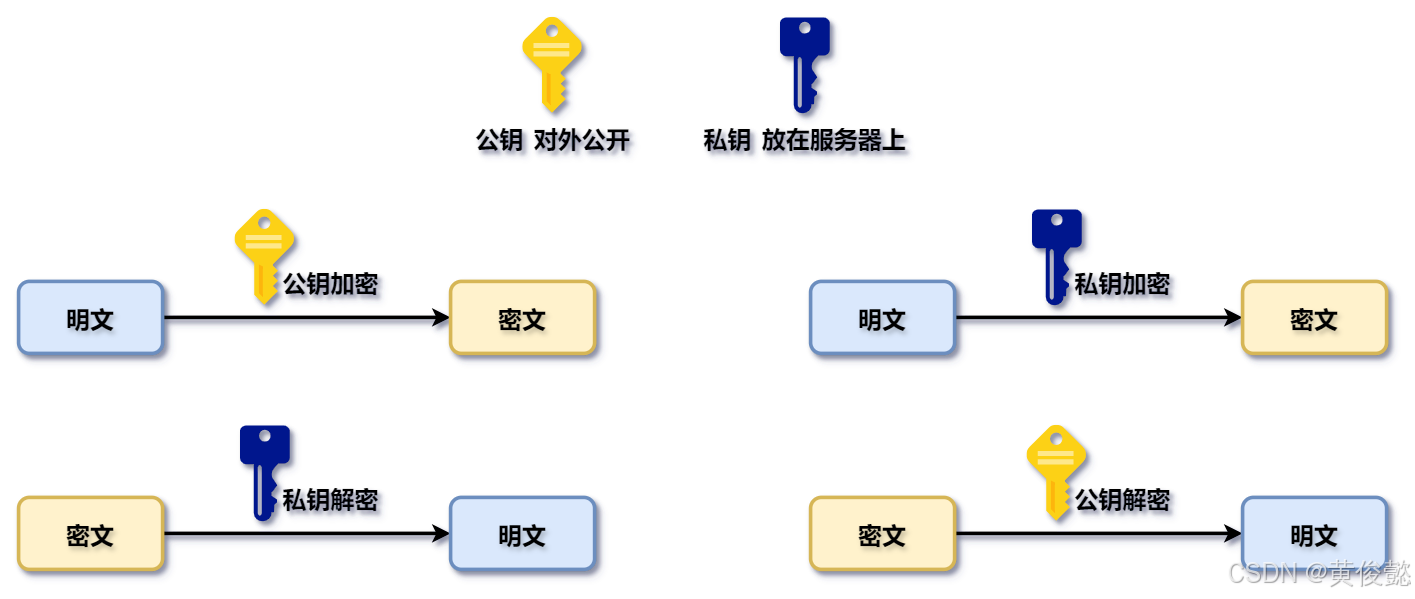
非对称加密就是加密和解密使用的密钥是不一样的，它有两个密钥，一个是公钥，一个是私钥。

公钥是对外界公开的，谁都可以拿到；私钥只有我自己知道，在我自己的服务器上。

然后呢，用公钥去加密的信息，只能用私钥去解；用私钥加密的信息呢，只能用公钥去解。并且你知道我的公钥，理论上是无法通过公钥来计算出私钥的。

它通常用在信息安全传输，以及用在数字签名的场合。

信息安全传输

在信息安全传输方面呢，我举一个例子。

我要把一个信息，在不被别人窃取的情况下，或者被别人窃取了，别人也不能拿它去使用的情况下，把它传递给对方。

画一个图：

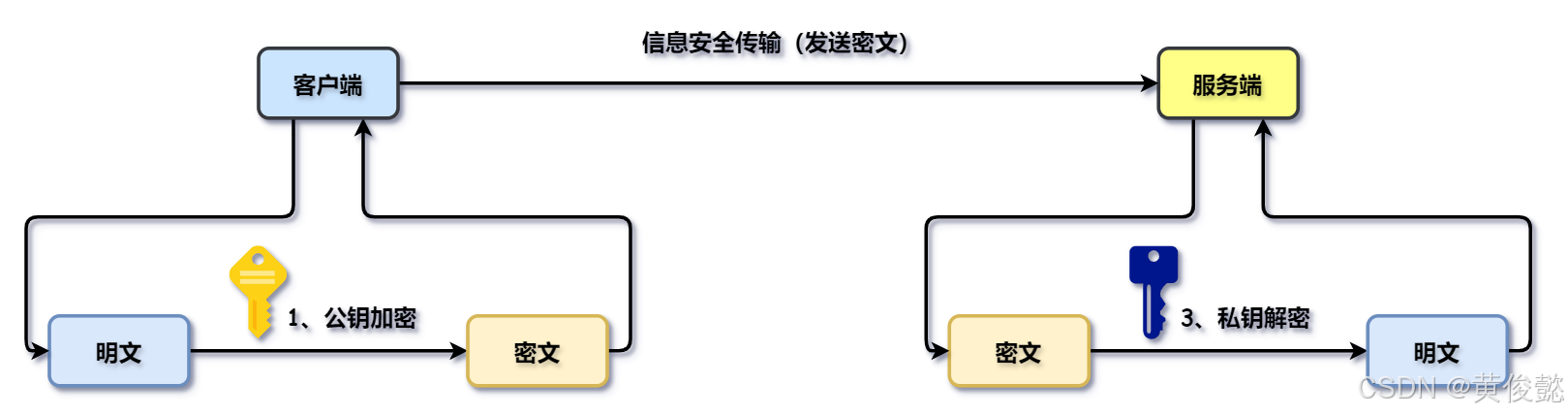
如何将信息从a地传播到b地，在传输的过程中保证安全，比如说信息发送者a通过公开渠道获得了信息接收者b的公钥，然后他就通过公钥把a要传递给b的信息进行加密，然后通过非安全的传输通道，将密文发送给b。那么大家想一下，如果说任何人从这个中间的传输通道上获取到的这个加密后的信息，它能解开吗？它解不开，因为通过b的公钥去加密的信息，只能通过b的私钥去解，所以说其他人拿到这个信息呢，也是没有任何用处的，因为只有b的私钥能解开。那么b得到这个密文之后，通过自己的私钥解开之后，就得到了对应的明文。这样的话就保证这个信息能安全的传给b。

数字签名

数字签名是什么意思呢？

大家想一下实际当中的一个场景，比如说我有一张票据，若干年前我刷个卡之后我要签个名，刷完之后商家会给你一个单子，说你要签名，比如说花了100块钱，我签个名，那么这个签名就是你的一个有效凭证，证明就是你本人刷的卡，这个叫做签名。

那么数字签名呢，就是说在网络中通过这种数字化的技术，来对我们所认可的信息做一种签名。

举一个例子。

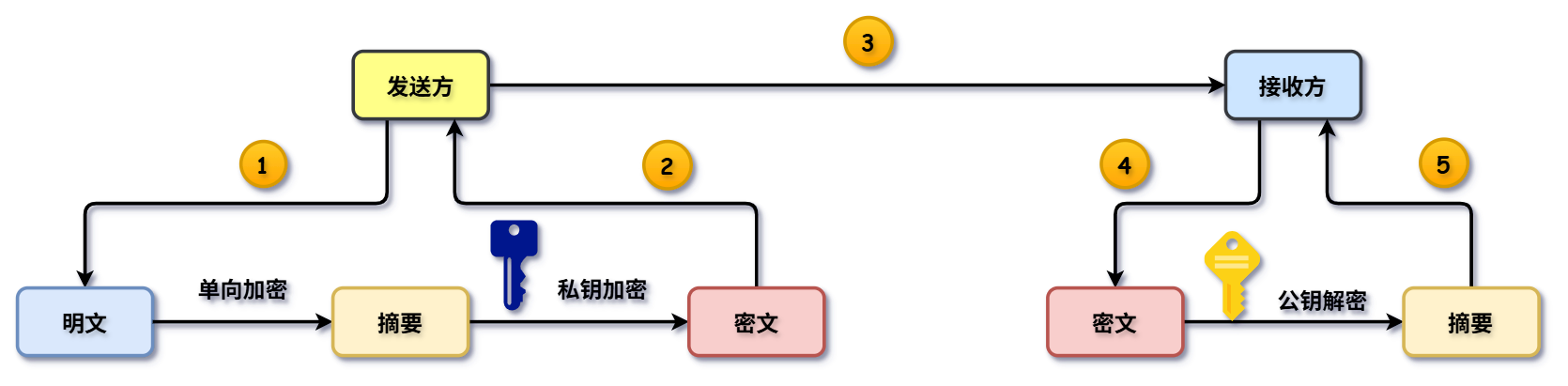
比如说我要对一段信息进行签名。首先是我这边的情况是我有两个东西，一个是公钥，一个是私钥。还有一个就是我要认证的一些信息，比如我承认这个信息的合法性。那么我用我的私钥对这个信息的一些摘要进行加密，一般是对摘要进行加密，然后把信息以及加密后的密文传播出去。那么接收方用我的公钥对信息进行解密，就能得到我签密之前的摘要。

实际工作中怎么做呢？我们来看一下啊。

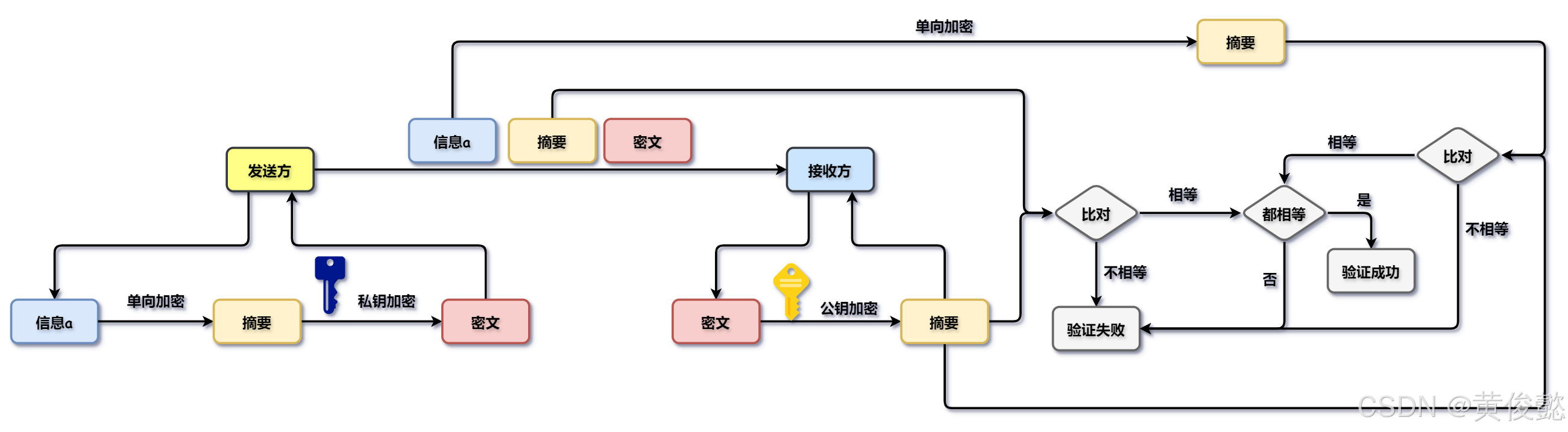
我要认证这个信息a，那么我先通过一个散列算法也就是单向加密，生成一个摘要。然后我通过我的私钥对摘要进行加密。然后把它变成一个密文，然后把它传播出去。大家可以看通过这么一种方式的话，如果接收方拿到这个信息之后，首先它是不是要拿着公钥对密文进行解密，得到一个摘要，然后得到这个摘要之后，和我传过来的摘要进行比对，如果相等，那么证明摘要是没问题的。同时，我再验证一下信息是不是能生成我这个摘要，如果根据我们前面所说的单向加密，如果信息不是原来的信息，那么它生成摘要是不正确的。

对称加密虽然有密钥的安全性问题，但是它的效率高；非对称加密呢，它的安全性高，但是它的效率低，我们在生产中呢，一般的情况下怎么用呢？

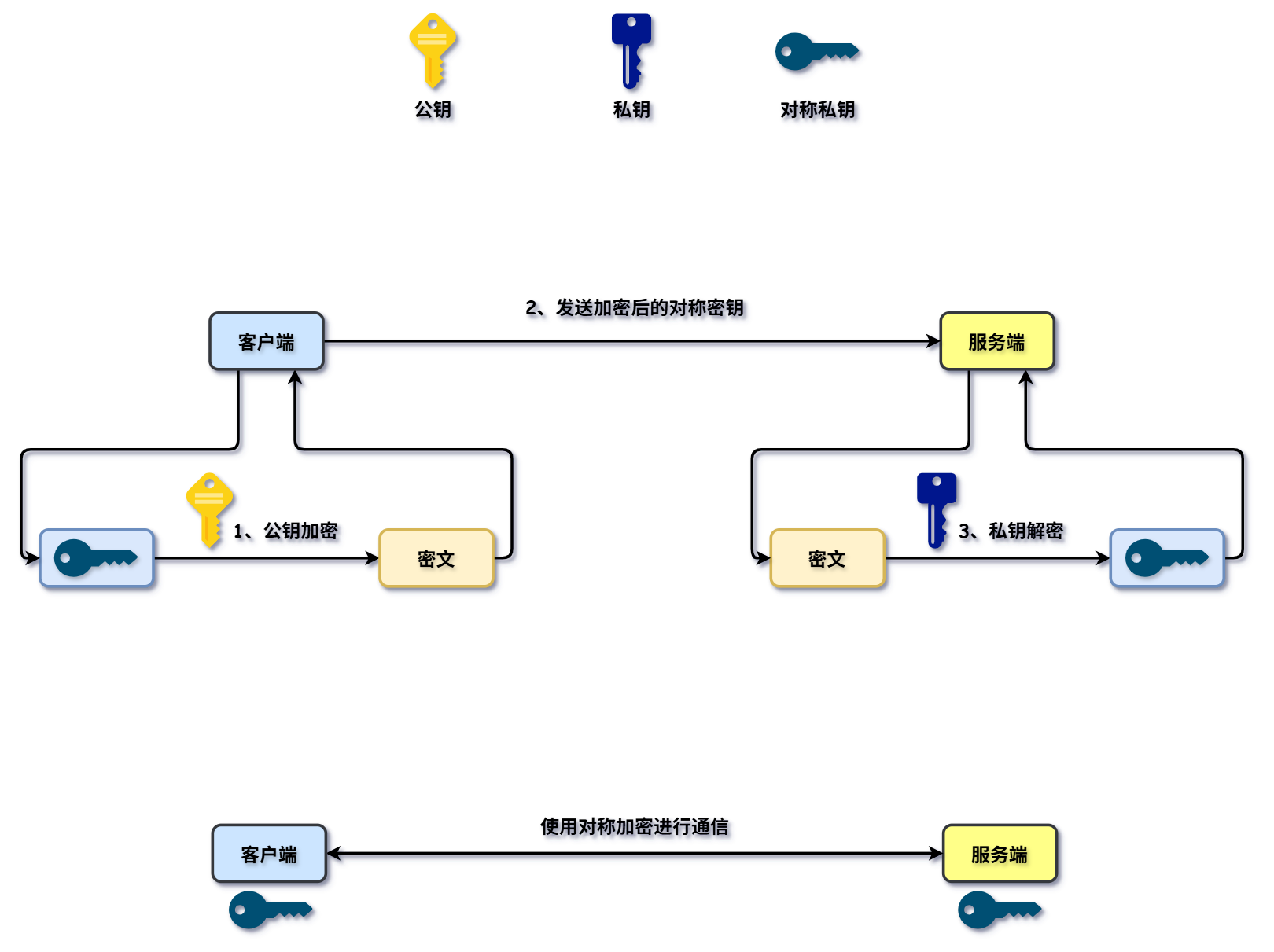
先使用非对称加密把密钥进行传输，就是说你和我之间，我们先用非对称加密的方式把密钥传传输给你，就是我知道这个密钥，然后我把它用非对称加密的方式传递给你，然后你也知道了。非对称加密是比较安全的，这样的话，通过安全的方式去传播密钥。然后我们再用我们共同知道的这个密钥来进行来做对称加密。这样的话，既保证了安全性，又保证了效率。

常用的非对称算法有RSA。其实我们在我们的https当中就是同时应用了对称加密和非对称加密。

密钥的管理

那么不管是对称还是非对称加密，其实最重要的是对密钥的管理。不管是对称加密的密钥，还是说非对称加密的公钥和私钥，如果说这些密钥一旦泄露出去，那么所有基于密钥的这些信息就失去了私密性。

信息的安全是靠密钥保证的，但在实际工中，在我们开发过程中，大部分公司，大部分中小公司，有的工程师把密钥直接写在源码当中，稍微好一些的工程师把密钥写在配置文件当中，其实写在配置文件当中是很常见的一件事情。

不管线上和开发环境是不是使用的同一套密钥，它是以一种明文的形式在我们的代码里写着的，不管是程序中还是配置文件中。这样的话，很多人都可以接触到，至少在公司内部，它不算一个秘密。这样的话，如果说哪个开发人员有点不太好的想法，那么他完全可以把密钥公布出去，虽然我知道一般没人去这么做，但是为了防止有些人这么做，作为一个架构师，你得考虑你项目的安全。

改善密钥安全，有两种手段。

加解密的服务

第一种手段是将密钥和加密算法放在一个独立的服务器上，甚至做成一个专用的硬件设施，对外提供加解密的服务。

画一个图。

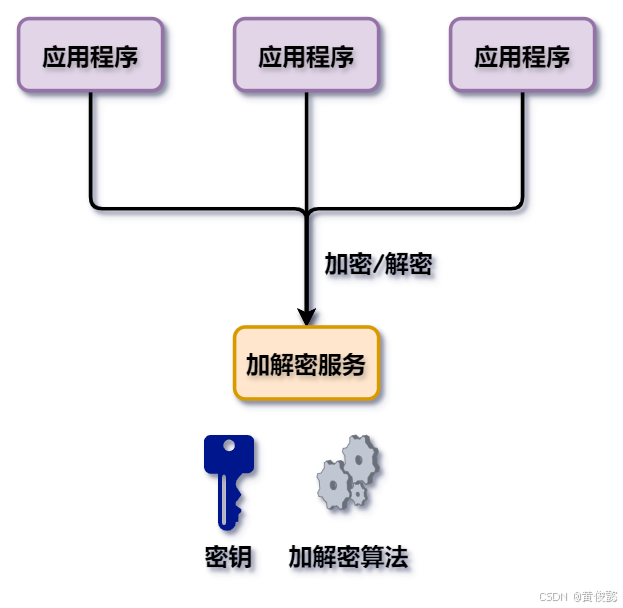
比如说这是我们的应用服务；然后还有一个服务专门做加解密的服务，加解密的算法和密钥都在这台机器上，这台机器知道的人肯定很少。然后应用程序需要用到加解密服务的时候，去调用它的接口来实现。这样的话，大部分开发人员开发的是应用程序，然后只有一少部分人来管理这个加解密的服务。这个服务由专人来部署，使密钥泄露的概率大大降低。

但是这种成本较高，因为我们需要有专人来管理。第一个是有专人来管理；第二个需要部署独立的服务；第三个它还可能成为应用的瓶颈，因为所有的应用如果要用到加解密服务都需要来调用它。

如果你的公司的用户量不是很大，服务之间调用量需要用到加解密的这种接口需求不是很多的话，可以考虑这种方式。

放在应用程序当中

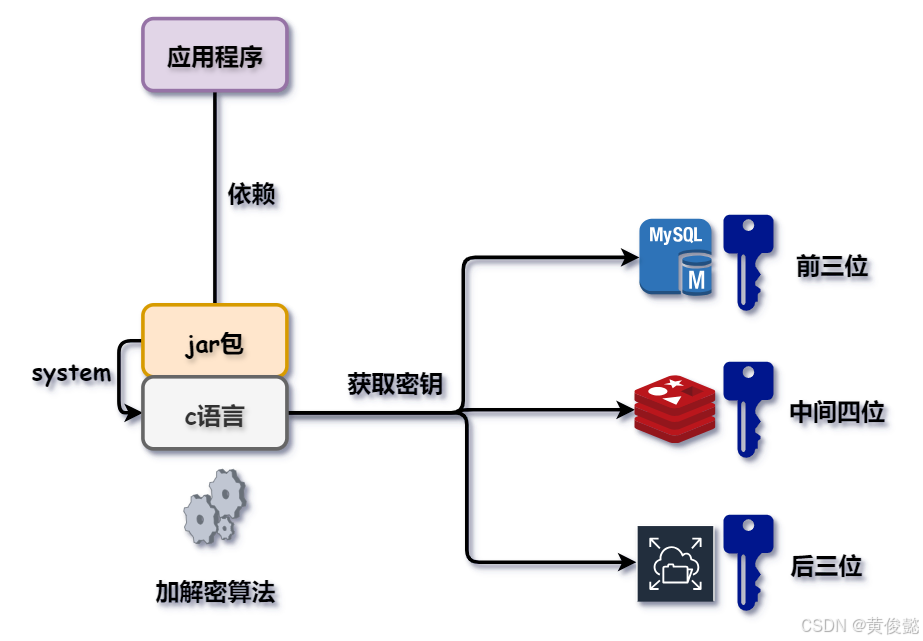
第二种方式是将加解密的算法放在应用程序当中。也就是加解密的算法就在应用程序当中，或者做成一个通用的jar包，被应用程序所依赖。

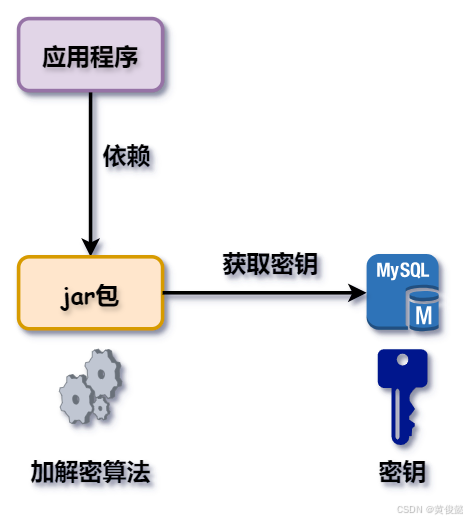
这个算法和应用程序是在一起的，但是我们要用到的密钥单独放在一个存储的地方，比如说存储在mysql里，存储在redis里，或者存储在文件服务器上。再狠一点的话呢，比如说密钥一共有十位，我把前三位是放在mysql当中，中间的四位放在redis当中，然后后三位放在文件管理服务当中。这样的话，别人是无法一下看到我们的密钥到底是是什么样子的。这样的话就兼顾了密钥的安全性，因为把它拆开存储，你要拿到这个完整的密钥，你得去三个地方去读取，而三个地方的权限不一定所有的人都有。

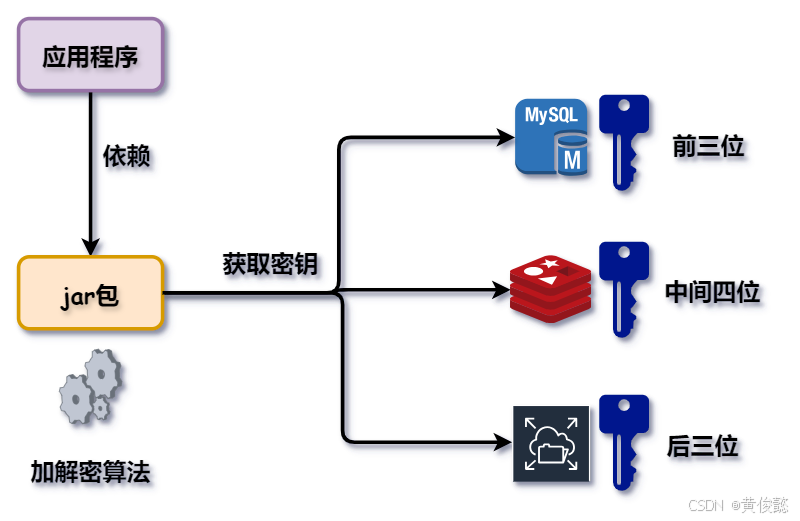
那么，如何说它也改善了性能呢？因为这种方式的加解密并不是集中在一个服务器当中，它是分散在各个应用当中，每个应用需要用到加密的时候，就去调用它这个算法。所以说这种方式，兼顾了性能和安全性。

如果说我们更再严格一点，开发应用程序的开发者，它依赖的这么一个jar包，它通过jar包的一个方法，传入一个明文，然后得到一个密文，这是正常人的做法。那么有一些人呢，它可以在加密算法的代码中把密钥打印出来，因为加密算法运行的时候肯定需要完整的密钥的，那么我在里面就把把它三个组装起来，直接打印到日志上，这样的话就能得到了。我把你的这个jar包的源码拆开，我在里面加一行代码打印出来，我就能获取这个东西。

因此，我们可以把这个架包做代码混淆。我们可以把jar包加密，加密之后别人也不是说能轻易读懂它的。这个加密算法，用其他的语言去编写，通过JAVA的system类库调c或者调其他语言，通过这种方式去做也是可以的。把它做成一个可执行的程序，对应用程序来说是一个黑盒子。