CF每日3题(1500-1700)

$a_i=(a_{i-1}+c)\mathrm{mod}m$是在模m意义下的等差数列

• 当m特别大，给的a本身就是等差数列，差是c
• $a_i+c>m>a_{max},$所以a的差除了正的c的也会有c-m
  所以讨论数组中的差判断就好

void solve(){int n;cin>>n;int mx=0;vector<int>a(n+1);set<int>s;forr(i,1,n){cin>>a[i];mx=max(a[i],mx);if(i>1){s.insert(a[i]-a[i-1]);}}if(s.size()==1||s.size()==0)return cout<<0<<endl,void();if(s.size()>2)return cout<<-1<<endl,void();int ne,po;ne=0,po=0;for(auto i:s){ne=min(ne,i);po=max(po,i);}if(ne<0&&po>0&&po-ne>mx){cout<<po-ne<<' '<<po<<endl;}else cout<<-1<<endl;}

题意：每个数的改变需要1s，求所给数倒计时到0改变的用时
如23，个位数的变化$0{\to }_{十位=1}^{10s}0{\to }_{十位=2}^{10s}0{\to }_{十位=2}^{3s}3$
所以每一位数变化的时间就是本位数和更高位组成的十进制数

/*
eg.12345
12345123412312
+   1
*/
void solve(){int n;cin>>n;vector<int>a(n+5,0),sn(n+5,0);string s;cin>>s;forr(i,1,n){sn[i]=s[n-i]-'0';sn[i]+=sn[i-1];//一个一个加会超时8e10 前缀和优化}forr(i,1,n){a[i]+=sn[n]-sn[i-1];// forr(j,i,n){//     a[id++]+=sn[j];// }}int c=0;forr(i,1,n){a[i]+=c;c=a[i]/10;a[i]%=10;}int bg=(c==0?n:n+1),fg=0;a[n+1]+=c;reforr(i,1,bg){if(!fg&&!a[i])continue;fg=1;cout<<a[i];}cout<<endl;
}

dp真难啊…

大佬题解
省流复述一下：
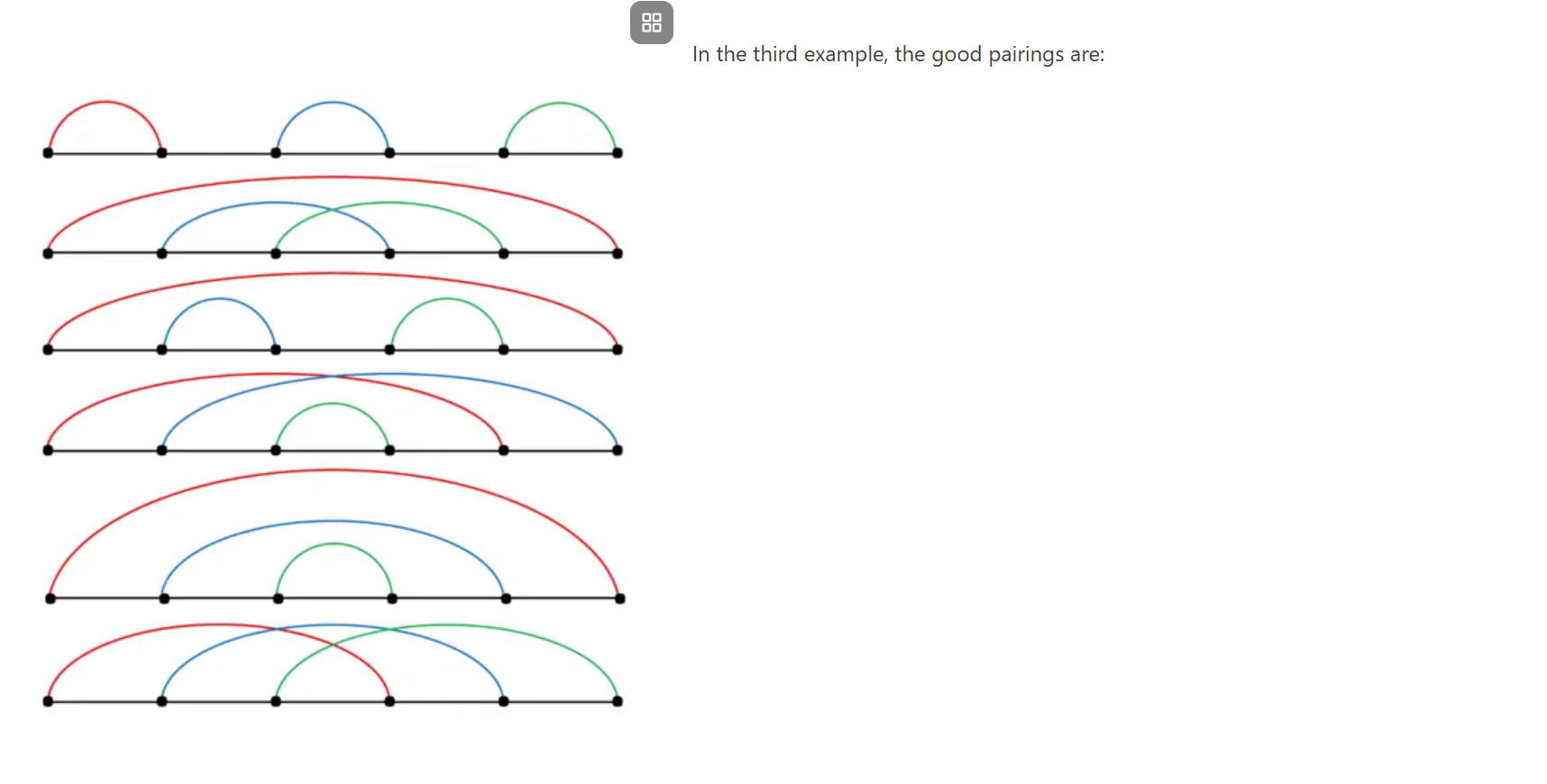
题意：2n个点两两相连，连线要求两两长度相等或相互包含
两个线如果不包含，相互交叉，就得相等
先考虑点1配对到点x形成一条线

• $x<=n$，线内有$x-2(<n)$个点，线外有$n-x(\ge n)$个，为了后面的点都能配对，线内所有的点都得连到线外，形成长度相等的线，只有不包含的情况。
  线内的配对完形成的线组总共长度是$x+x-2=2x-2$，n中可以有多个这样的组，x-1需要整除n
  整除n的地方会有1贡献，设此贡献为$d[n]$
• $x>n$，有包含的情况，文章中枚举分析的很好理解，直接粘了
  
  $dp[i]=\sum _{j=0}^{i-1}dp[j](前缀和)+d[i]$

void solve(){int n;cin>>n;vector<int>dp(n+1,0),d(n+1,0);forr(i,1,n){//找1~n每个数的因子for(int j=i;j<=n;j+=i)d[j]++;}dp[1]=1;int sum=dp[1];forr(i,2,n){dp[i]=(sum+d[i])%mod;//x>n的情况+x<=n的情况sum=(sum+dp[i])%mod;//更新前缀和}cout<<dp[n]<<endl;
}