并查集理论基础, 107. 寻找存在的路径
并查集理论基础
并查集常用来解决连通性问题。
大白话就是当我们需要判断两个元素是否在同一个集合里的时候,我们就要想到用并查集。
并查集主要有两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合
Q1: 判断两个元素是否在同一个集合里为什么不用集合,或者用数组呢?
元素分门别类,可不止一个集合,可能是很多集合,成百上千,那么要定义这么多个数组或集合吗?
Q2: 并查集是如何判断两个元素在同一个集合里的?
假设现有三个元素A,B,C (分别是数字),现在三个元素A,B,C要放在同一个集合,其实就是将三个元素连通在一起,如何连通呢?只需要用一个一维数组来表示,即:father[A] = B,father[B] = C 这样就表述 A 与 B 与 C连通了(有向连通图)。
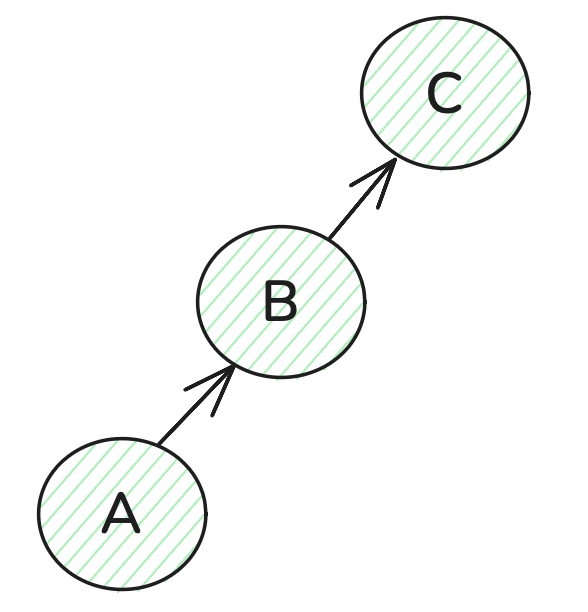
如何判断A和B是在同一个集合内,判断其根节点是否一致。给出A元素,就可以通过 father[A] = B,father[B] = C,找到根为 C。给出B元素,就可以通过 father[B] = C,找到根也为为 C,说明 A 和 B 是在同一个集合里。
那C如何表示?由于C本身就是根节点了,因此C设置为 father[C] = C,即自己指向自己。这样的话,就将三个元素A,B,C放在了同一个并查集里面了。
并查集代码实现
节点初始化
// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
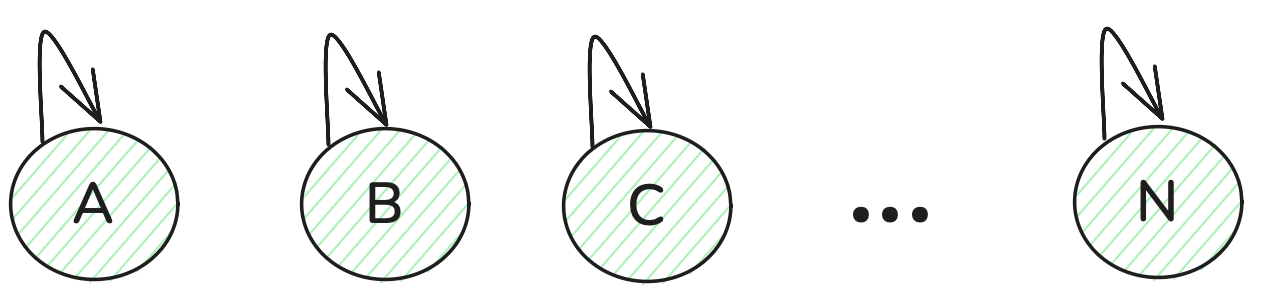
}给定N个元素,我们要将其放到一个并查集内,那第一步就是初始化一个并查集,其中每个元素都指向自己,此时这N个元素各自构成了一个独立的小并查集,后续就是把这些并查集进行合并操作。
节点寻找
// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u; // 如果根就是自己,直接返回else return find(father[u]); // 如果根不是自己,就根据数组下标一层一层向下找
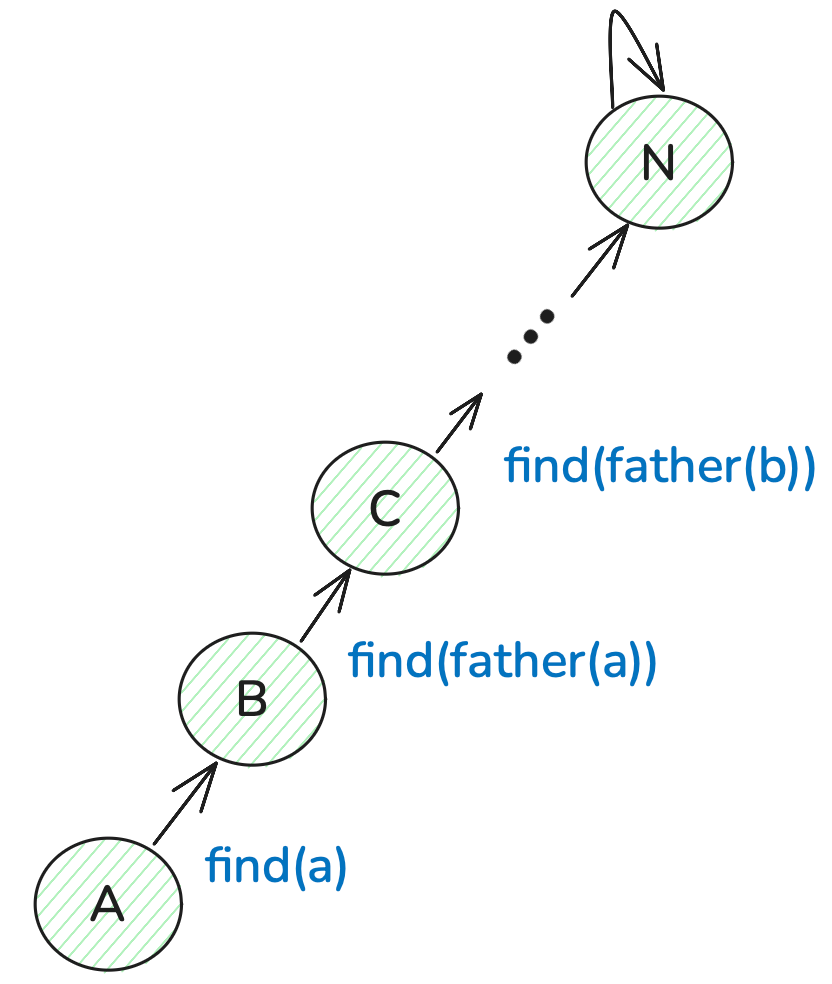
}寻根的过程就是不断向上遍历的过程。不断遍历,当节点指向自己时,此时就说明了遍历到了根节点。在这里就可以看到了一些问题了,因为你要不断向上遍历,因此如果深度较大的话,那递归的次数就很大了,因此后续可以基于这点进行优化,将这颗树修改为又矮又胖。
优化:路径压缩
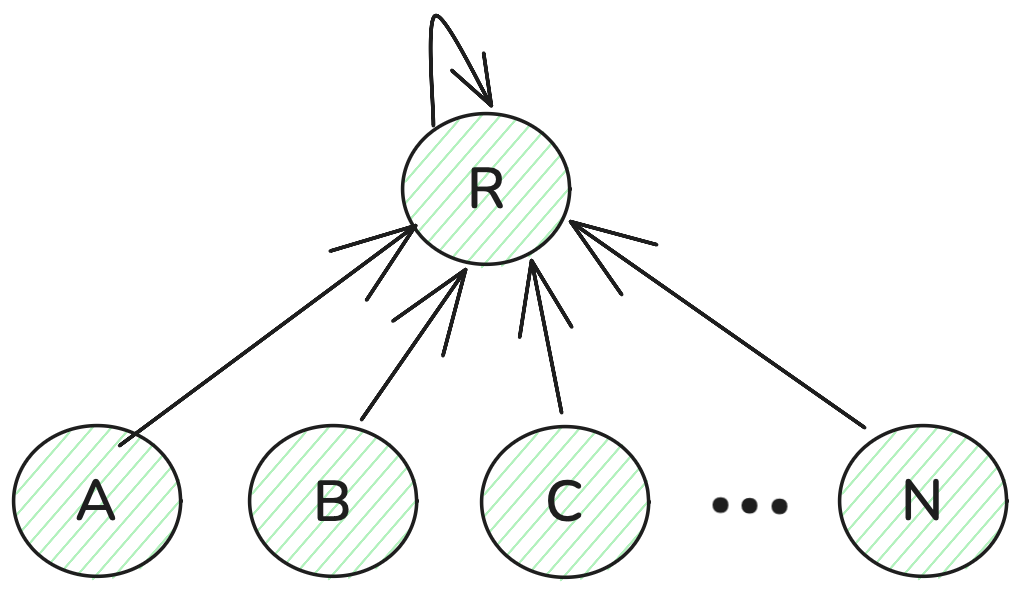
为了实现将这颗树改为又矮又胖,我们可以在find()函数内进行修改。为什么不在节点添加部分进行路径压缩,主要是节点添加部分其实是一个深度增大的过程,这部分需要先找到根节点,之后继续在根节点基础上进行拓展,而在find()中已经保证了该元素一定在并查集内,因此可以在这部分进行路径压缩的工作。
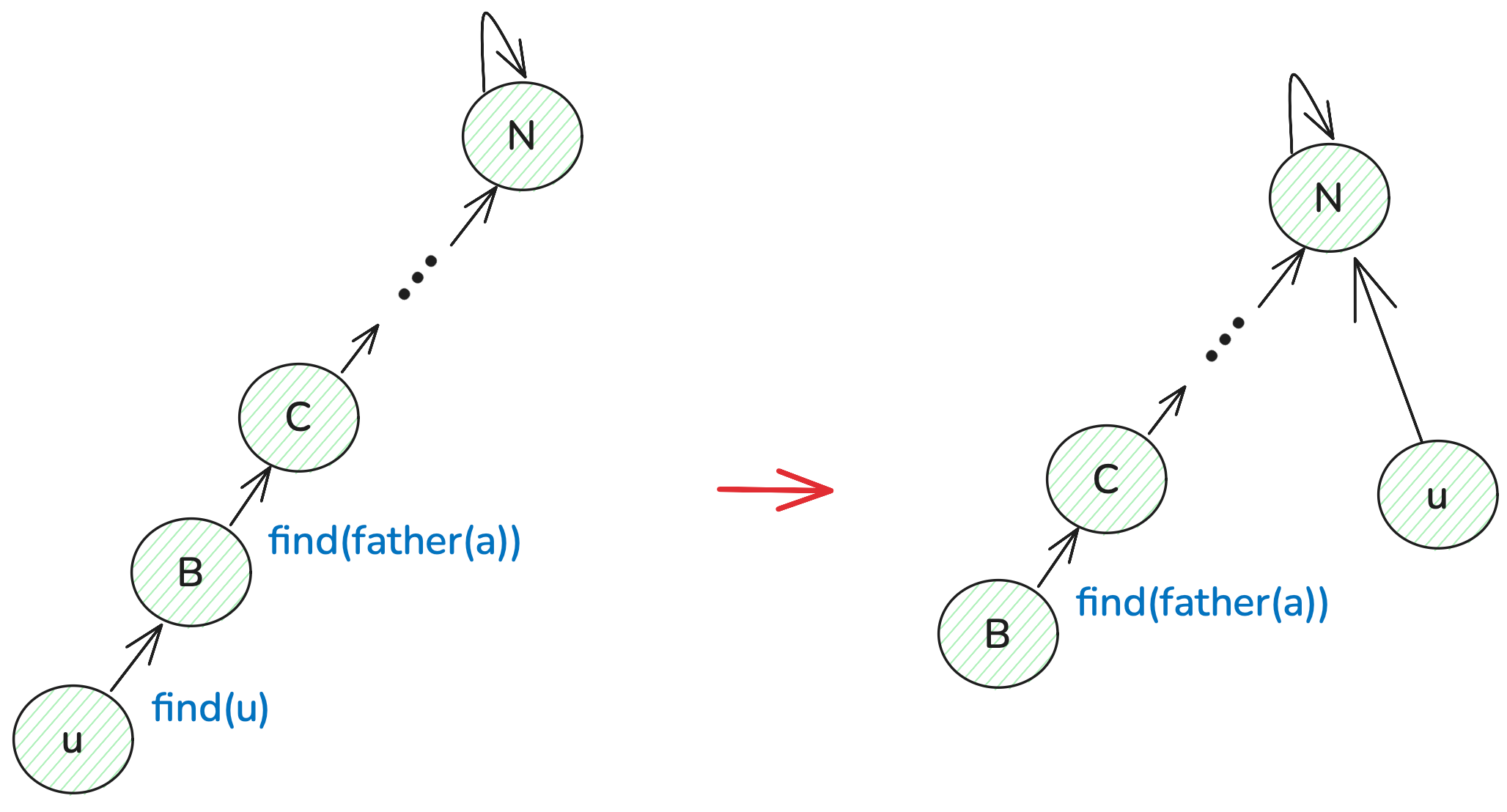
// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u;else return father[u] = find(father[u]); // 路径压缩
}find(father[u]): 是不断向上遍历,终止条件是 u ==father[u]), 此时 return u,因此find(father[u])最后得到的是并查集的根节点。而father[u]是表示u的父节点,father[u] = find(father[u])表示u直接连在根节点之下。这样就减少了后续递归的深度。
节点添加
// 将v,u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}往并查集添加节点前,需要先判断这个节点是否已存在于并查集中,如果已经存在了,那就不用添加了。如果不存在,则将当前节点 v 指向 根节点。
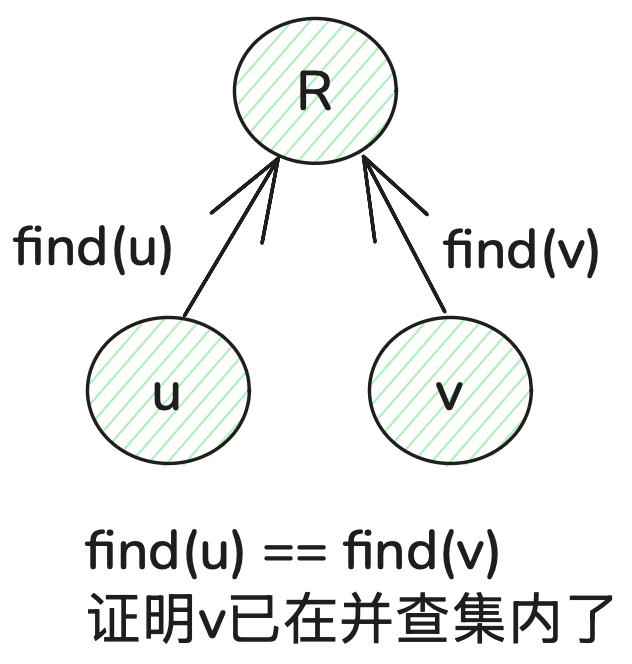
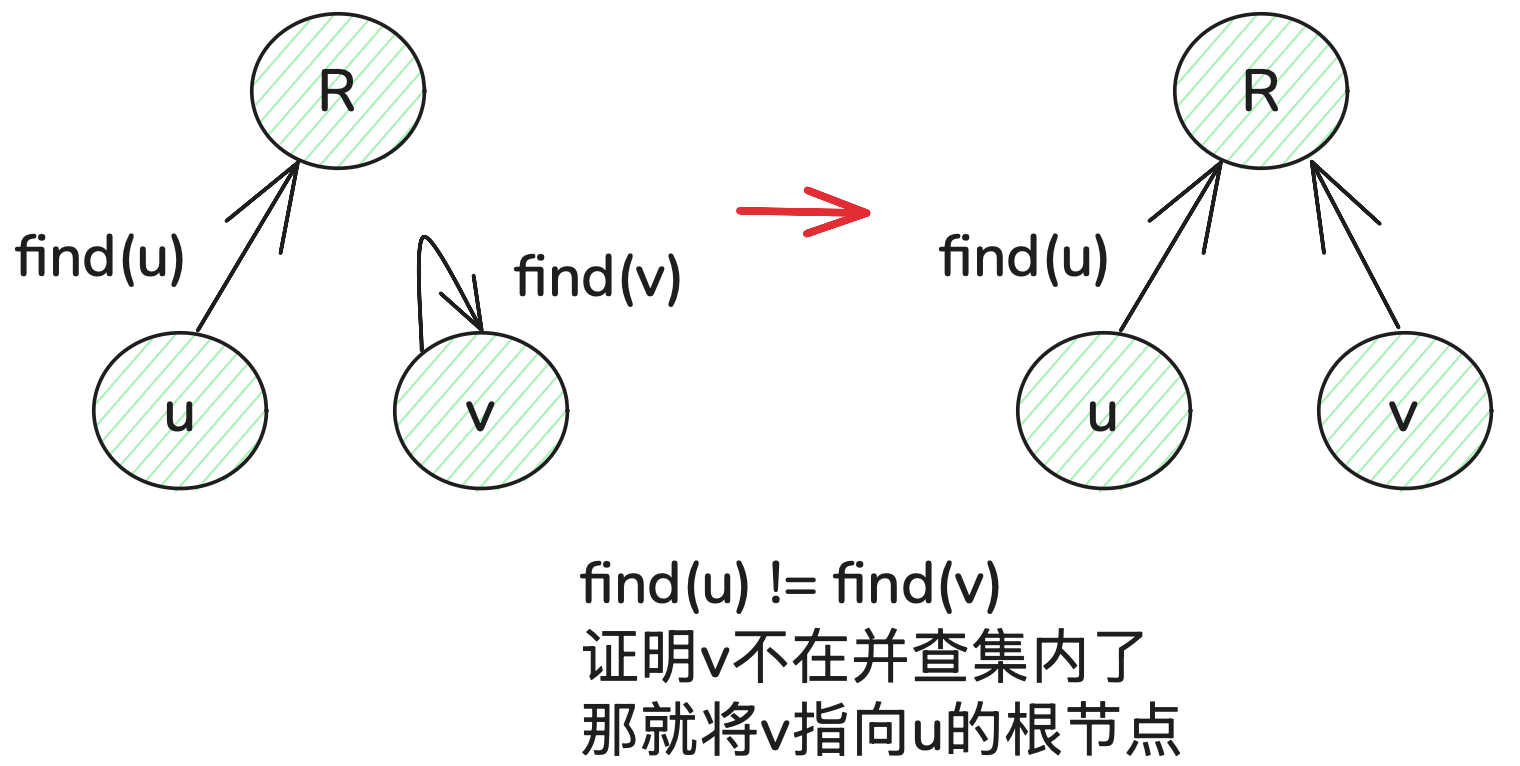
两个节点是否在同个集合内
根节点是否相同。
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}易错点:
### 版本1
// 将v,u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}### 版本2
void join(int u, int v) {if (isSame(u, v)) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回father[v] = u;
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}为什么不用版本2的join函数呢?因为join前也需要判断两个元素是否已经在同个并查集内的操作。这两个的实现逻辑是不同的。
以下述代码执行流程进行举例说明:
join(1,2)
join(3,2)版本2的执行,其构成的并查集如下所示。可以看到其实虽然代码是顺序执行的,但其实执行的功能是类似于并行的效果。先判断1和2根节点不同,随后将2的根节点设置为1,即2指向1。随后2和3的根节点也不同,因此2指向3。
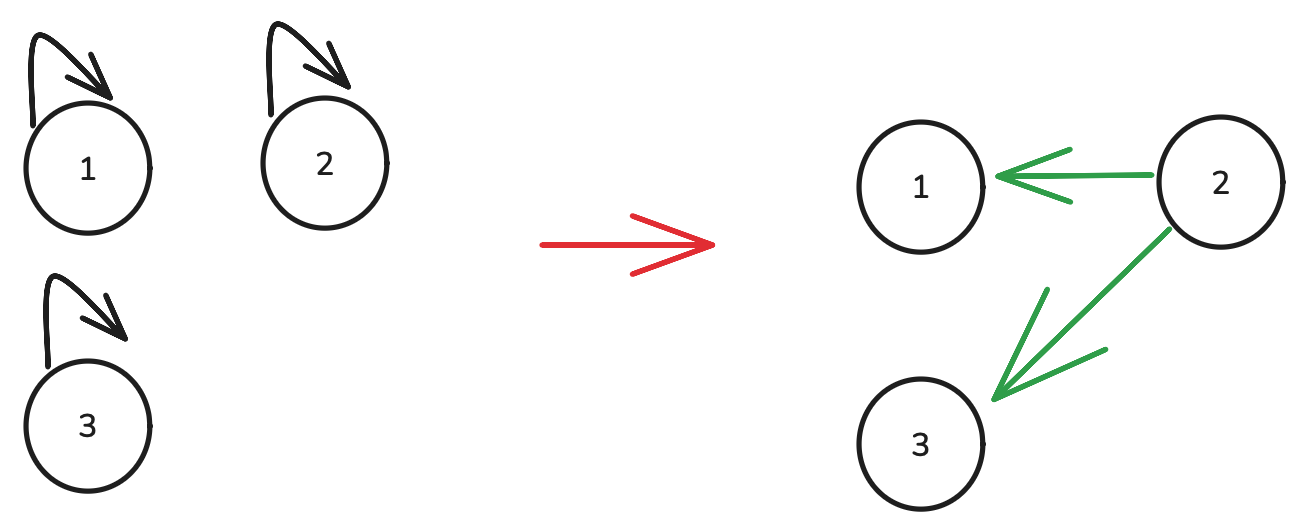
而如果是版本1,则其构成的并查集如下所示。
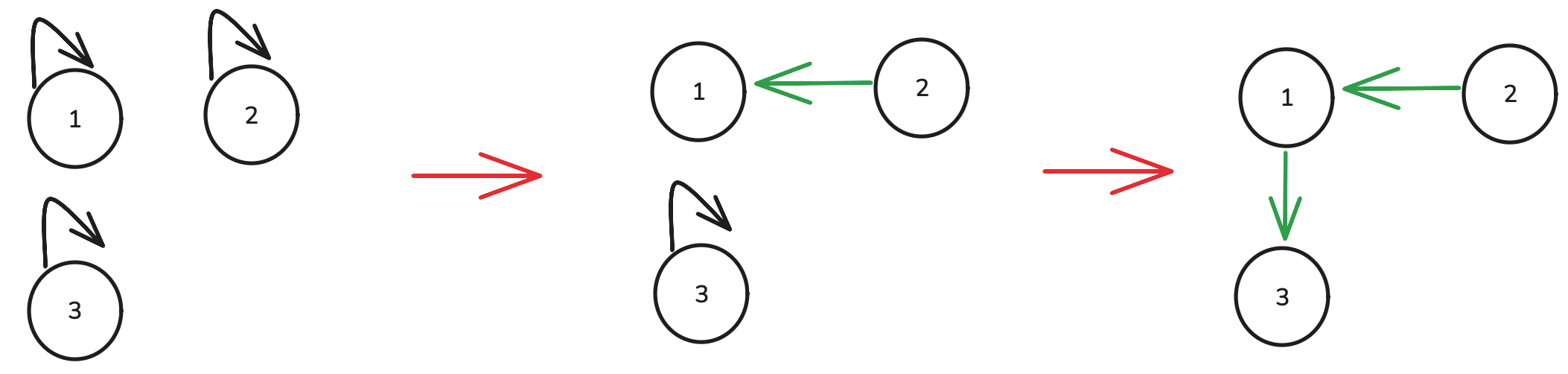
先判断1和2根节点不同,随后将2的根节点设置为1,即2指向1。随后2和3的根节点也不同,但此时与版本2最大的不同在于v到底是谁,v=find(v),你输入的v是2,但经过find(2)后输出的是1,因此此时v变为1了,此时再进行连接操作的话则是在1的基础上指向3。
像版本1这样操作的话就保证了并查集中的图是强连通的关系。
107. 寻找存在的路径
并查集的应用
思路:是否存在从节点 source 到节点 destination 的路径 转换 为节点 source 和节点 destination是否存在同一个并查集。
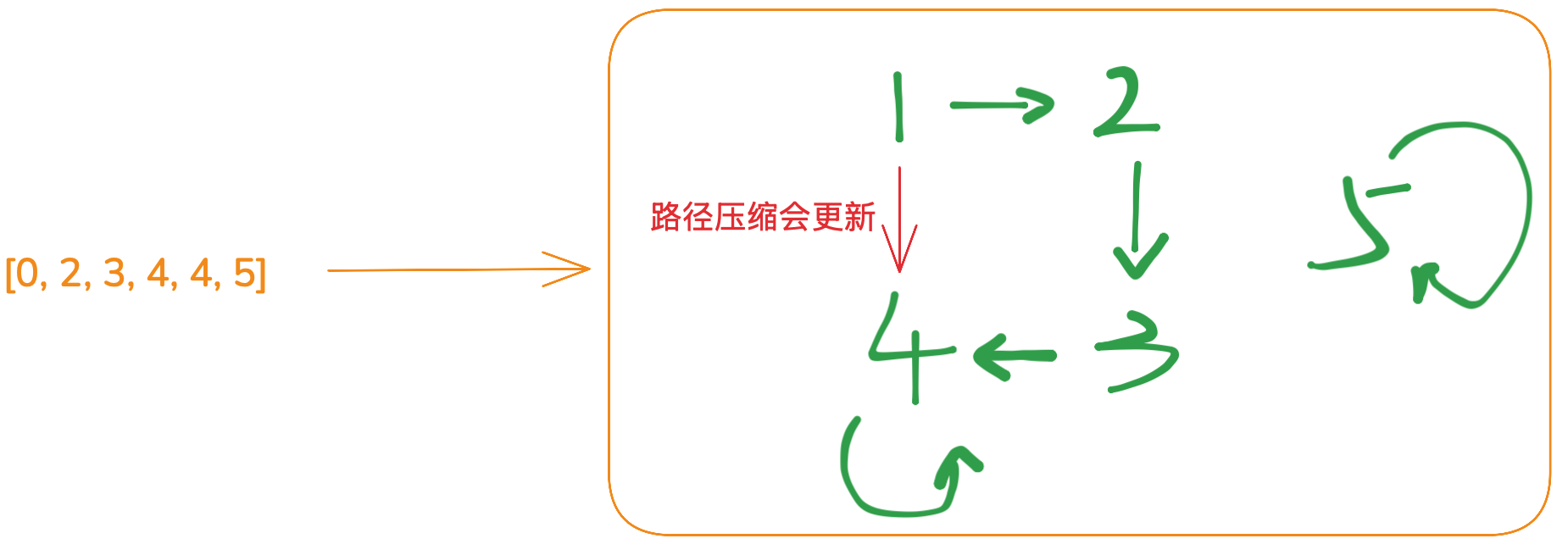
并查集底层的数据结构还是数组
Code
class UnionFind:def __init__(self,node_size): """创建一个类的实例时, __init__方法会自动被调用"""self.father = list(range(node_size+1))## 等同于以下实现# self.father = []# for i in range(node_size+1):# self.father.append(i)def find(self, node): """实现找到node的根节点"""if self.father[node] == node:return nodeelse:# self.find(self.father[node]) ## 往上递归查询根节点self.father[node] = self.find(self.father[node]) ## 路径压缩,将node直接指向根节点return self.father[node] ### 返回根节点def join(self, node, add_node):"""node, 并查集内已经存在的点add_node, 准备添加的点添加的点是指向的节点,因此 root_node_1 -> root_node_2"""root_node_1 = self.find(node)root_node_2 = self.find(add_node)if root_node_1 != root_node_2: self.father[root_node_1] = root_node_2def is_Same(self, node_1, node_2):"""判断两个节点是否在同个并查集内"""root_node_1 = self.find(node_1)root_node_2 = self.find(node_2) if root_node_1 == root_node_2:return Trueelse:return Falsedef main():node, edge = map(int, input().split())solution = UnionFind(node) ### 初始化并查集for _ in range(edge):cur_node, next_node = map(int, input().split())solution.join(cur_node, next_node)source, destination = map(int, input().split())if solution.is_Same(source, destination):print(1)else:print(0)if __name__ == "__main__":main()