数据结构初阶:排序算法(二)交换排序
🔥个人主页:胡萝卜3.0
🎬作者简介:C++研发方向学习者
📖个人专栏: 《C语言》《数据结构》 《C++干货分享》
⭐️人生格言:不试试怎么知道自己行不行

前言:在数据结构初阶:排序算法(一)中分析了插入排序(直接插入排序和希尔排序)和选择排序(直接选择排序和堆排序)两类算法,详细说明了其基本思想、代码实现和时间复杂度,接下来我们学习交换排序算法的相关内容。
目录
四、交换排序
4.1 冒泡排序
4.2 快速排序
4.2.1 hoare版本
4.2.2 挖坑法
4.2.3 lomuto前后指针法
4.3 快速排序--非递归
4.3.1 代码
4.3.2 代码解释:
四、交换排序
4.1 冒泡排序
冒泡排序(Bubble Sort)是一种简单直观的排序算法。它通过重复地遍历要排序的数列,一次比较两个相邻的元素,如果它们的顺序错误就交换它们的位置。这个过程会一直重复,直到没有需要交换的元素为止,也就是说数列已经排序完成(不断比较当前下标和下边的下一个进行对比,把筛选的数据对换)
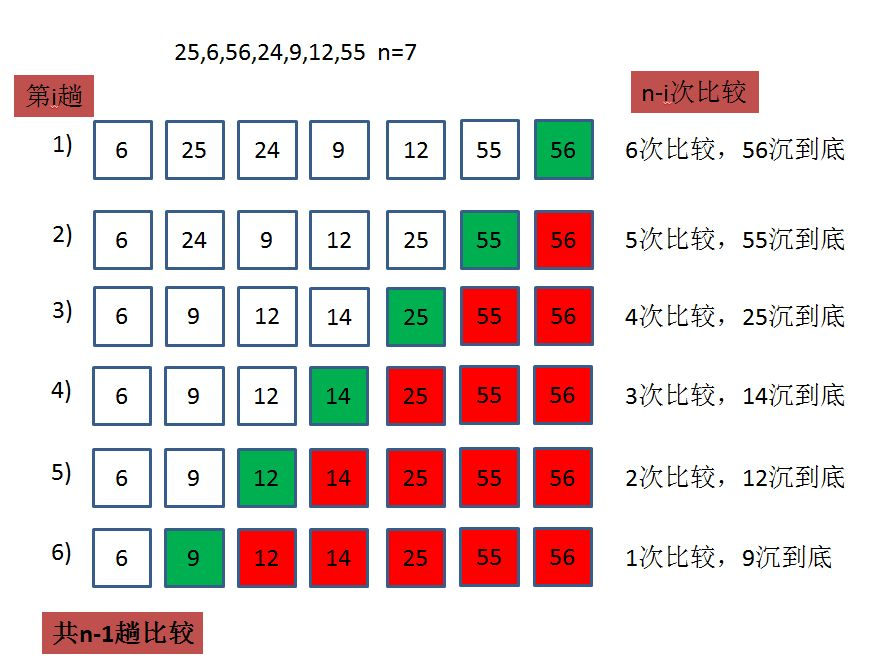
4.1.1 代码
void BubbleSort(int* arr, int n)
{//趟数for (int i = 0; i < n; i++){//交换次数for (int j = 0; j < n-1-i; j++){if (arr[j] > arr[j + 1]){swap(&arr[j], &arr[j + 1]);}}}
}4.1.2 冒泡排序的特性总结
1、时间复杂度:O(N ^ 2);
2、空间复杂度:O(1);
3、冒泡排序是一种非常容易理解的排序,具有教学意义;
4、稳定性:稳定。
4.2 快速排序
快速排序是hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程,直到所有元素都排在相应位置上为止
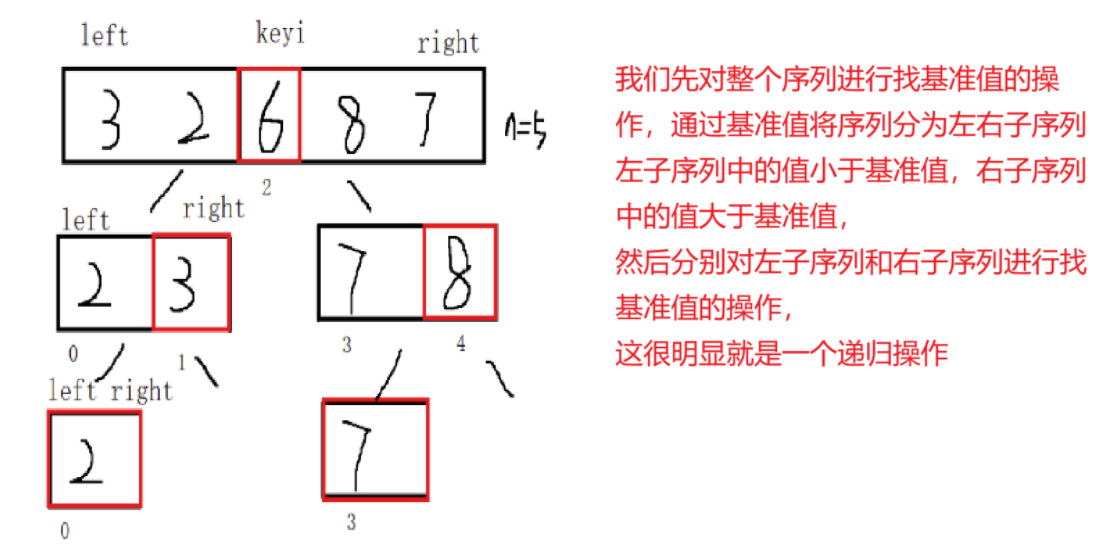
根据上面的基本思想,我们就可以得到快速排序算法的大致框架:

这时候就有同学想问了,这个递归函数的结束限制条件是怎么得来的?
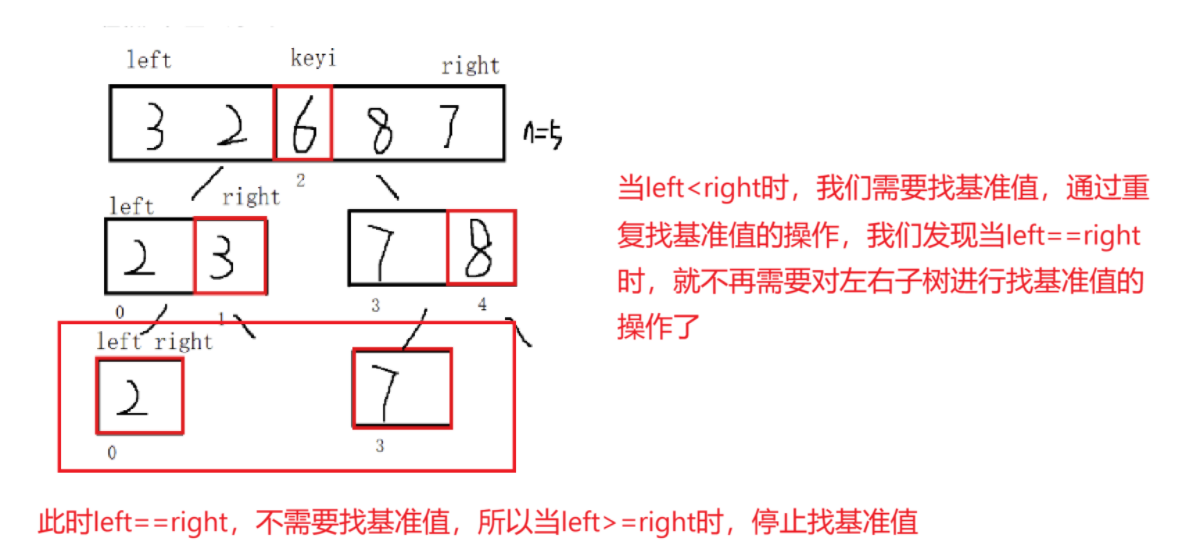
那这个时候就有个问题了,怎么找基准值呢?我们聪明的先辈想出了三种找基准值的方法,接下来,让我们一一学习:
4.2.1 hoare版本
算法思路:
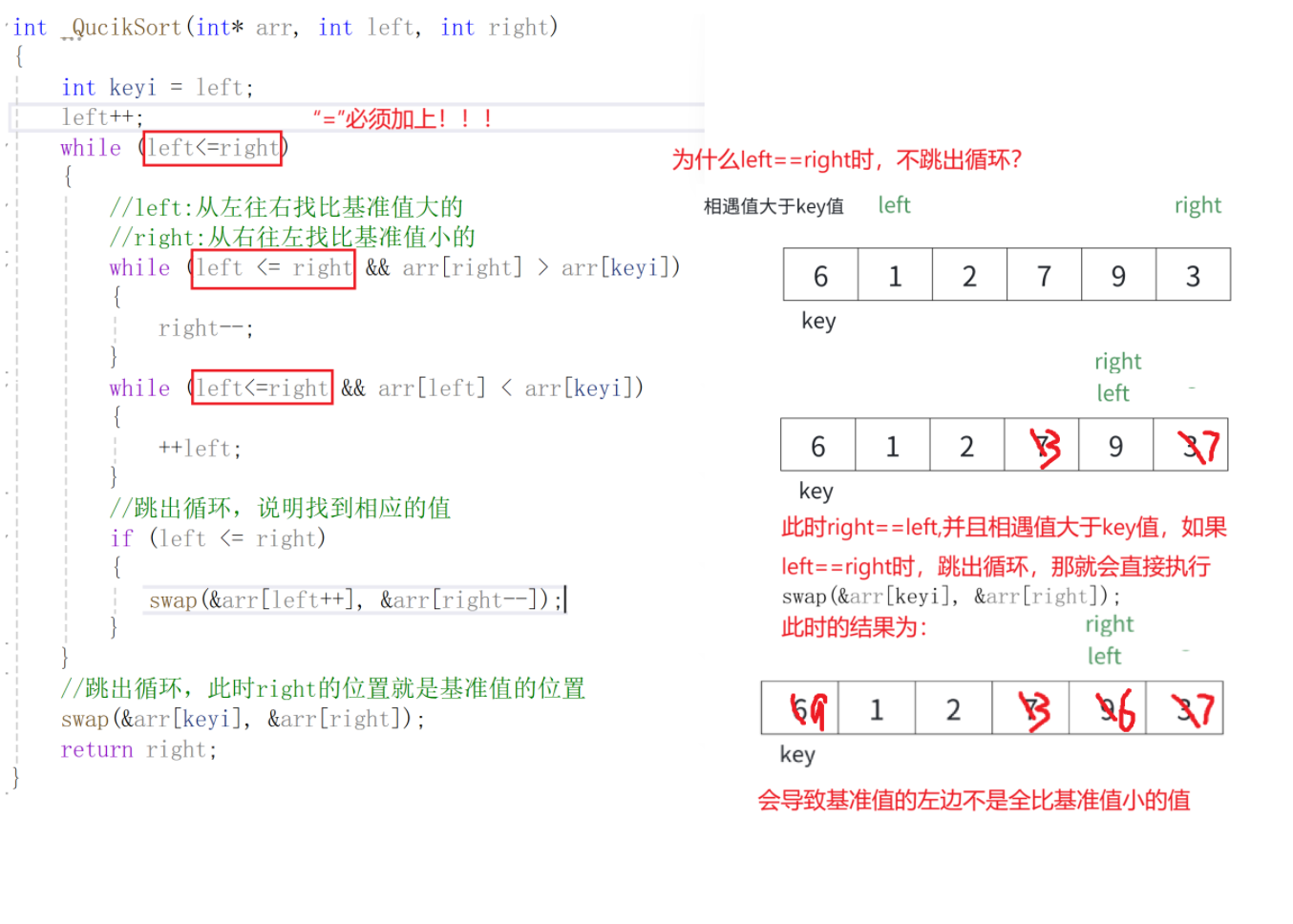
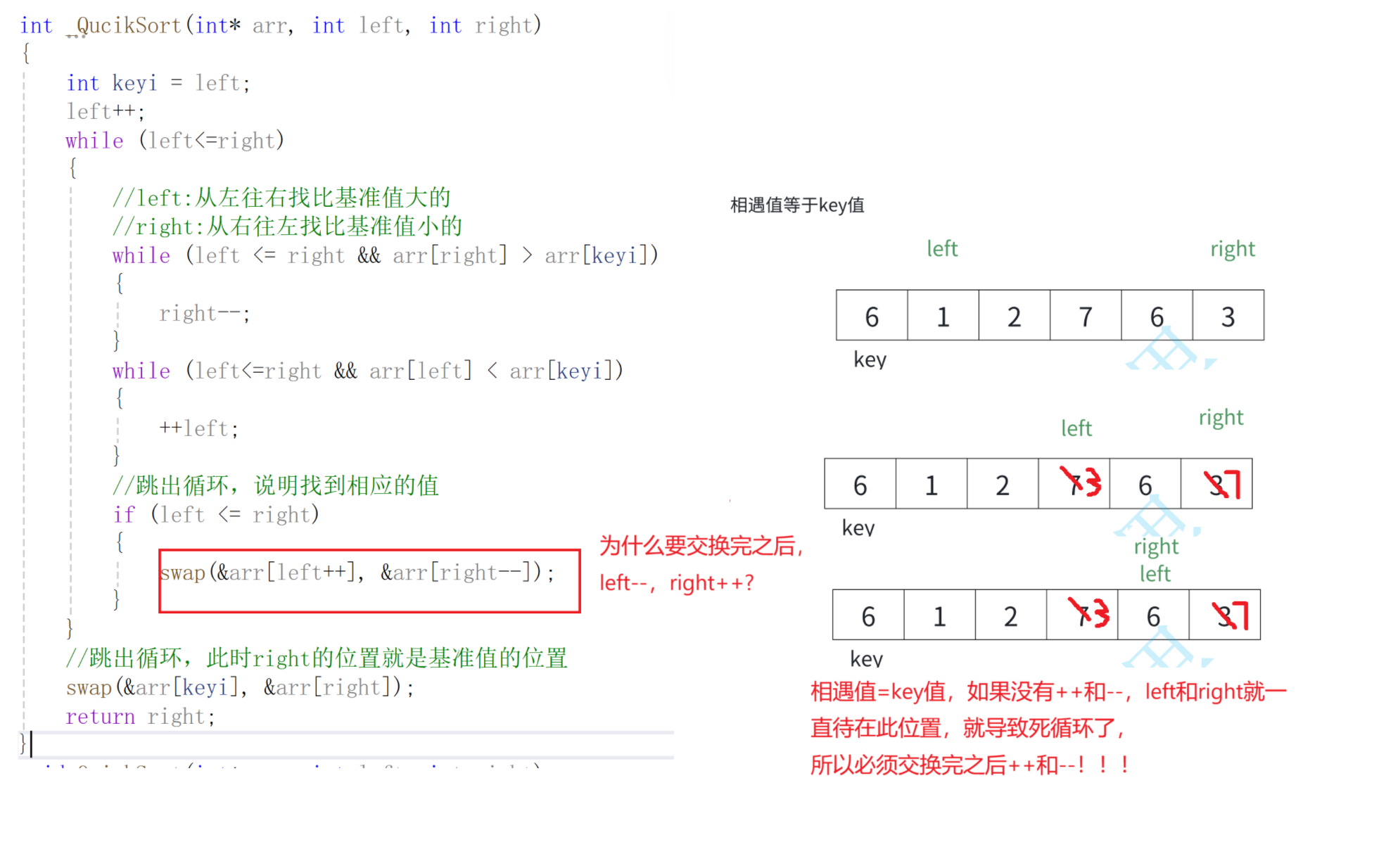
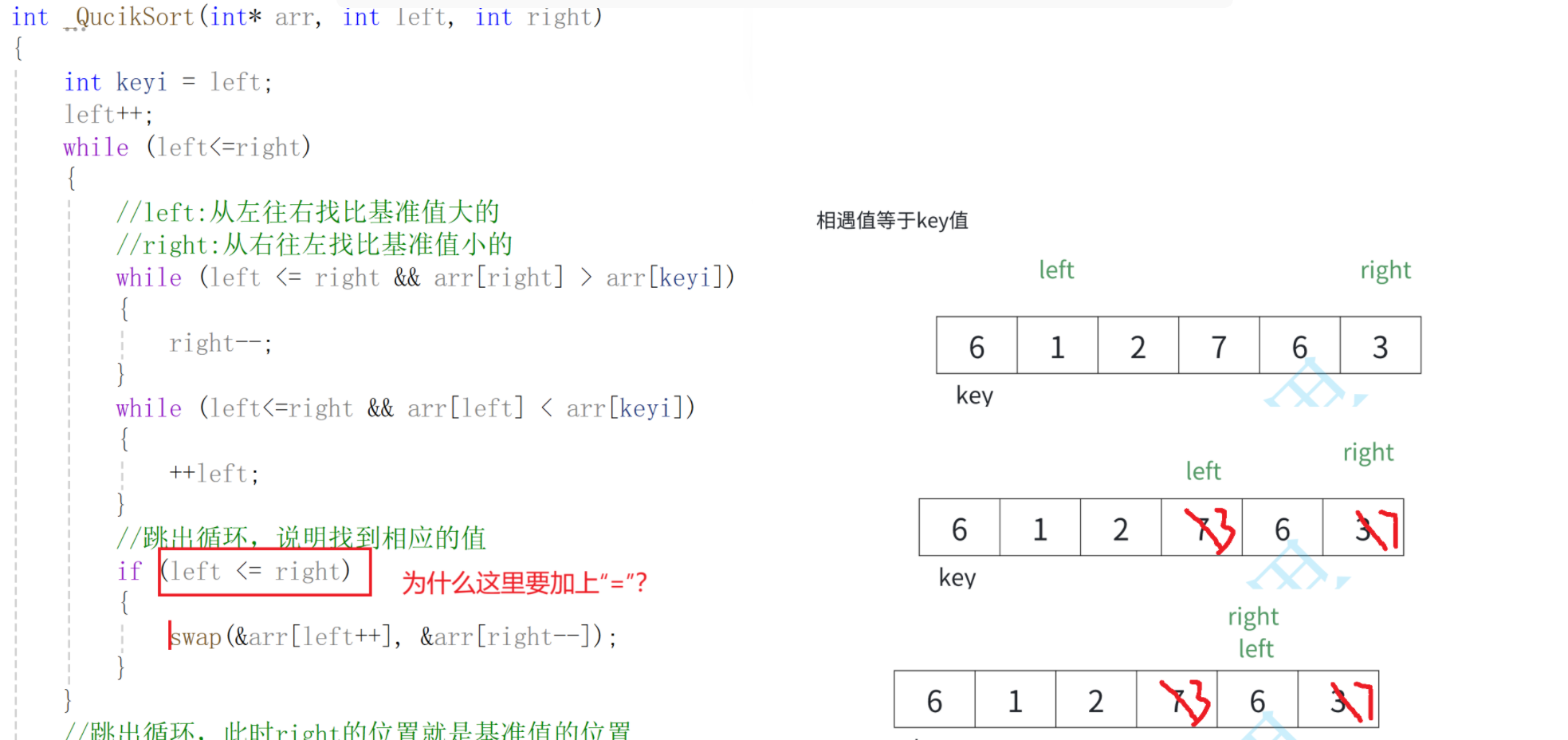
首先将0索引的位置作为基准值,创建左右指针,左指针从索引值为1的位置开始从左往右找比基准值大的值,右指针从右往左找比基准值小的值,找到之后,交换左右指针指向的数,交换完之后,左指针++,右指针--(必须做),重复此操作,直到左指针大于右指针,此时交换右指针所在的位置和默认基准值的位置(刚开始假设的0索引位置)右指针所在的位置就是基准值的位置,此时左边都是比基准数小的,右边都是比基准数大的,再依次递归基准数左边部分和右边部分,就实现了排序。
注意:一定要先从右边开始找比基准数小的,先从左边开始就无法达到效果
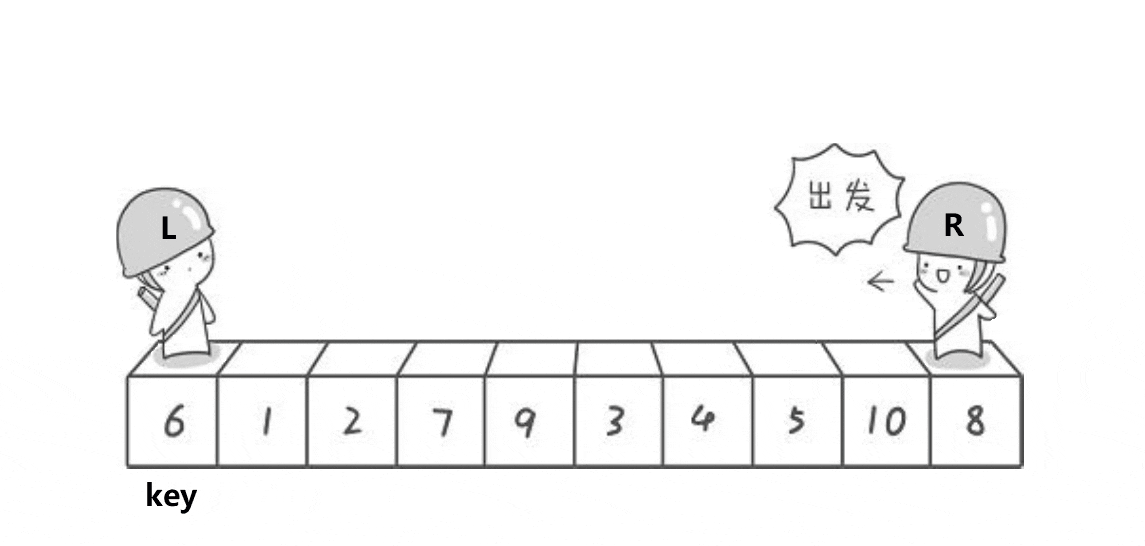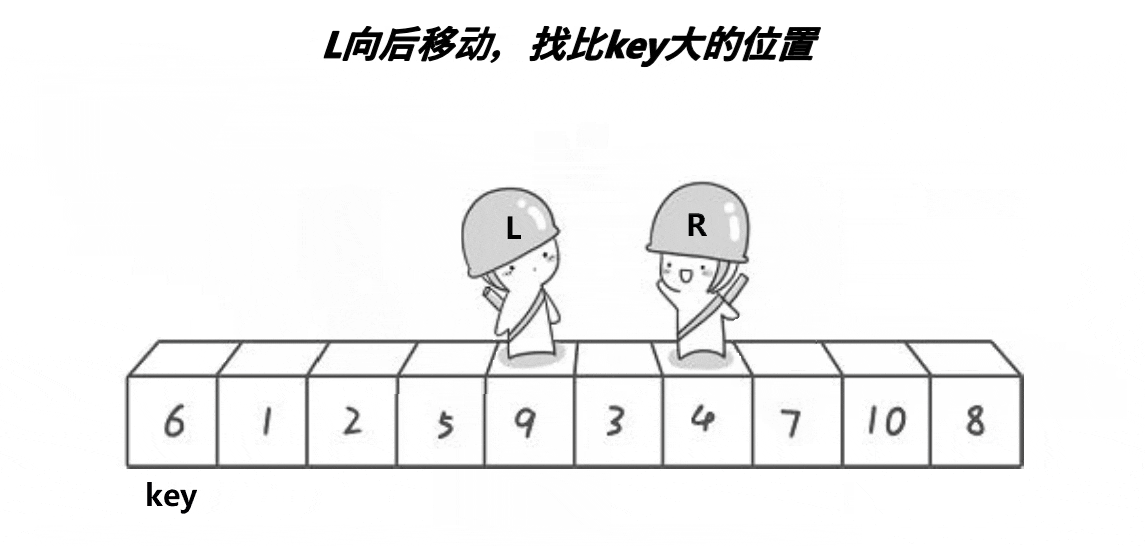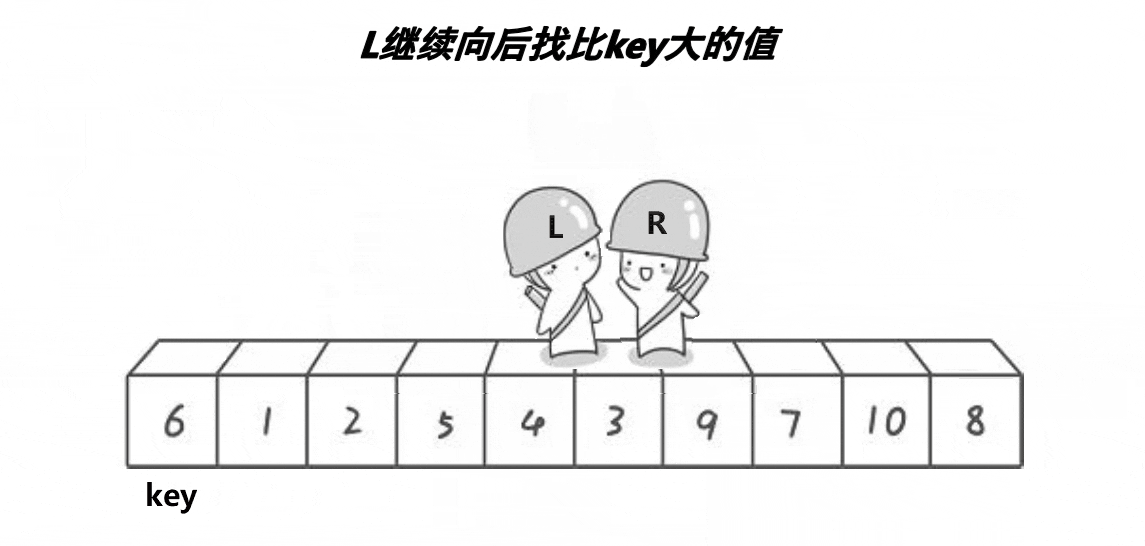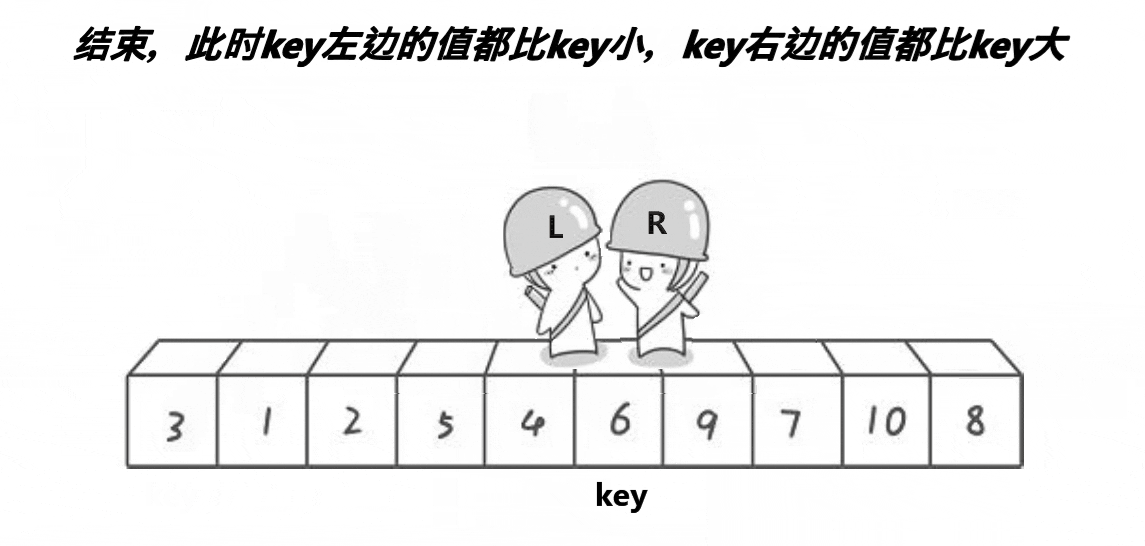
代码实现:
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
int _QucikSort(int* arr, int left, int right)
{int keyi = left;left++;while (left<=right){//left:从左往右找比基准值大的//right:从右往左找比基准值小的while (left <= right && arr[right] > arr[keyi]){right--;}while (left<=right && arr[left] < arr[keyi]){++left;}//跳出循环,说明找到相应的值if (left <= right){swap(&arr[left++], &arr[right--]);}}//跳出循环,此时right的位置就是基准值的位置swap(&arr[keyi], &arr[right]);return right;
}
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值--keyiint keyi = _QucikSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}接下来,我们来看几个问题,通过这个问题的学习,我们可以更好的掌握代码。
问题1--内层循环为什么不能加上“=”?
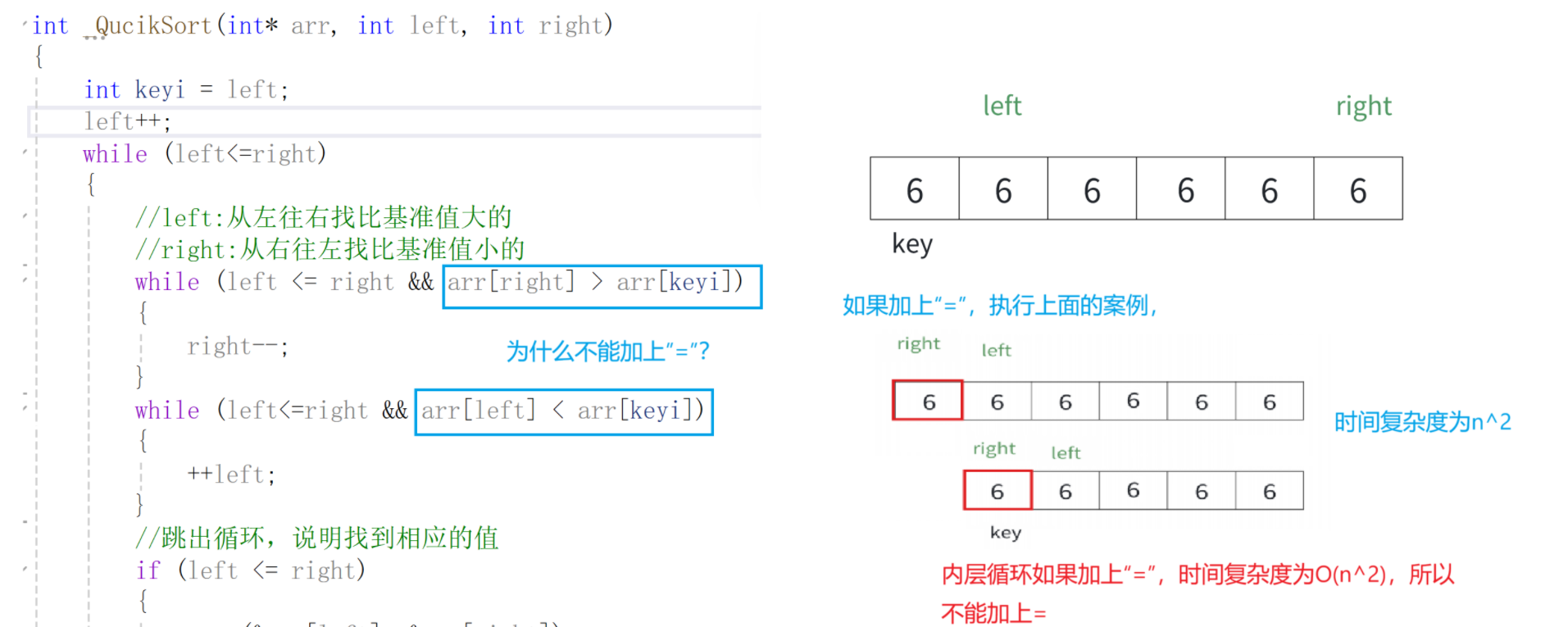
问题2--为什么left==right时,不跳出循环?
问题3--为什么交换完之后,left++和right--?
问题4--为什么if语句中要加上“=”?
4.2.2 挖坑法
单趟的动图演示:
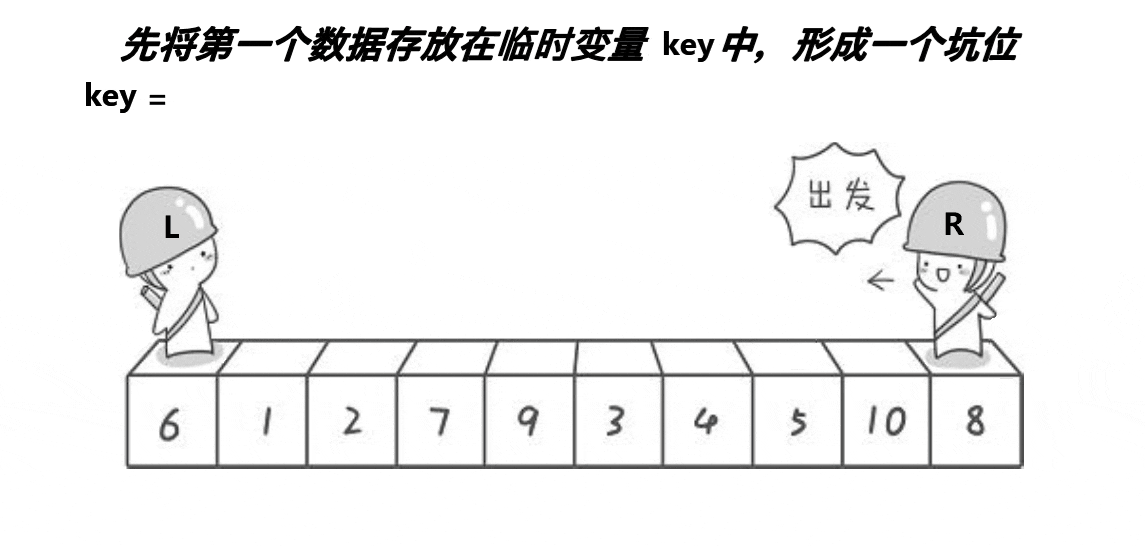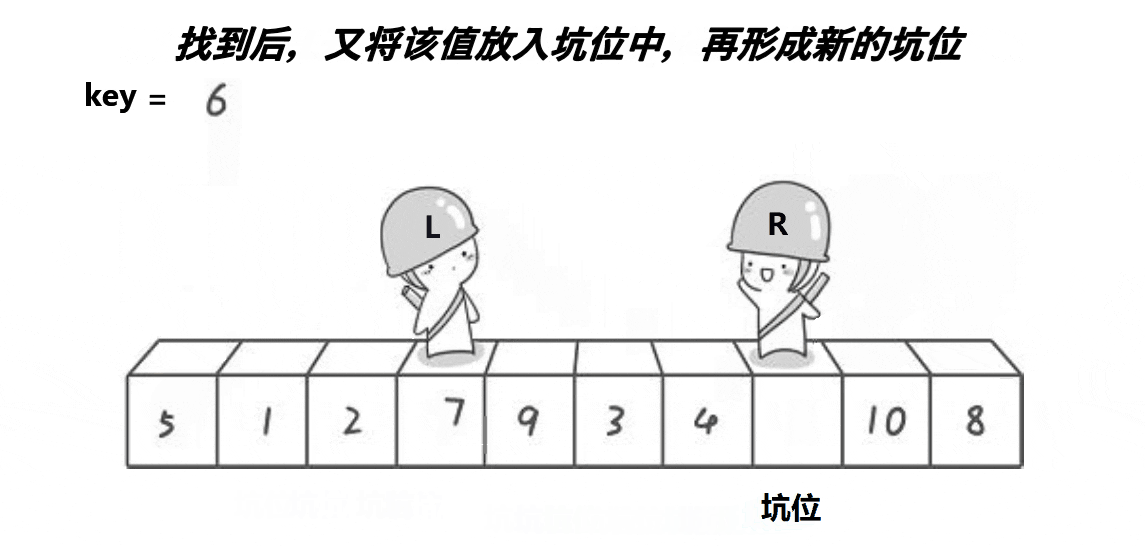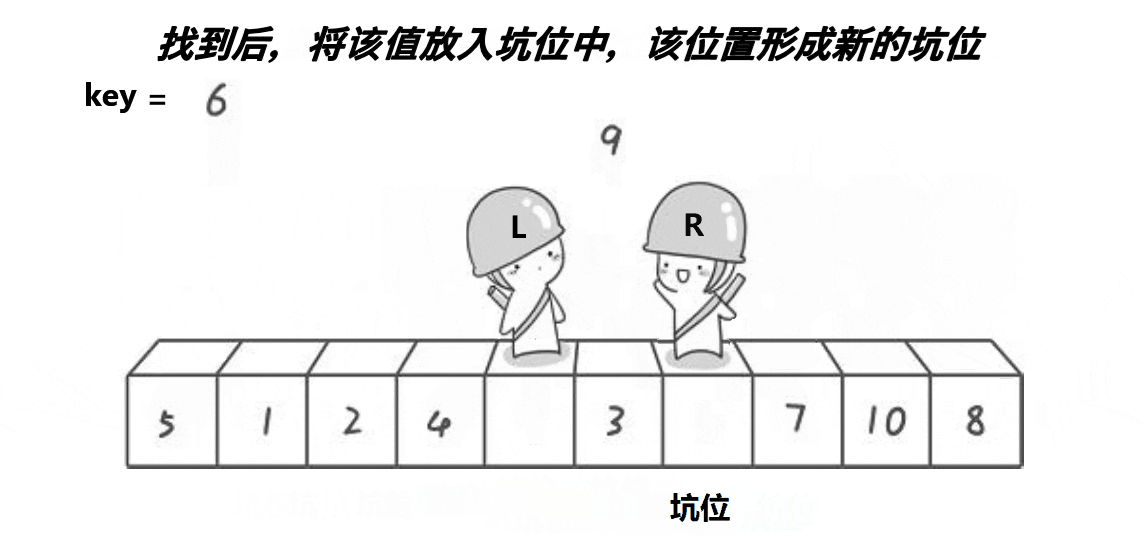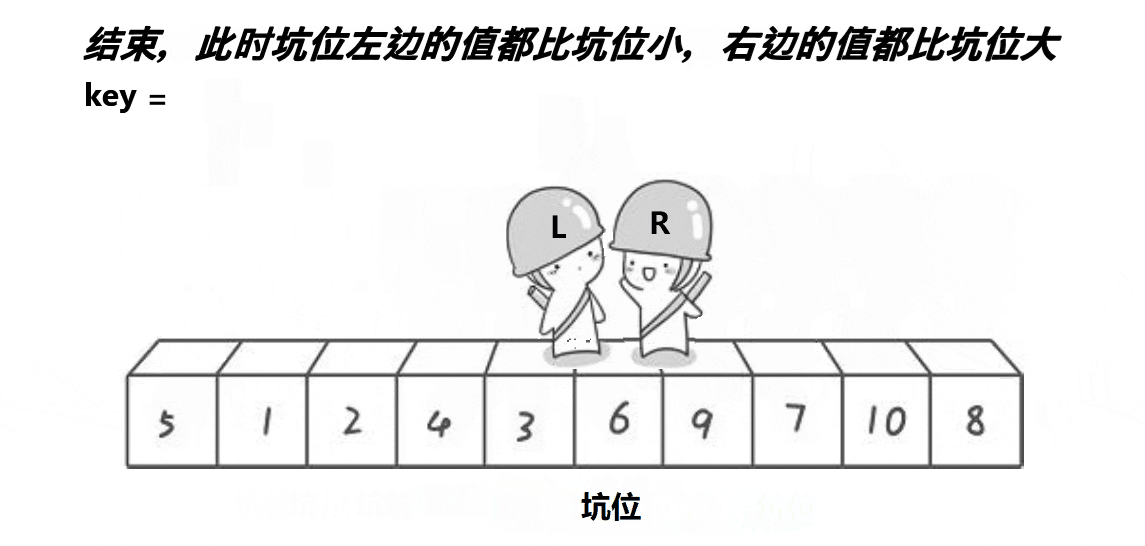
思路:
创建左右指针。首先将0索引的位置作为坑位,坑位所在的值作为基准值,右指针从右往左找比基准值小的值,找到之后立即放到坑中,让该右指针所在的位置成为新的坑位,左指针从左往右找比基准值大的值,找到之后立即放到坑中,并让该左指针所在的位置成为新的坑位,重复上面操作,直到左右指针相遇,相遇的坑位为基准值的位置,返回当前坑的下标
代码
int _QucikSort(int* arr, int left, int right)
{int hole = left;int keyi = arr[hole];while (left < right){while (left < right && arr[right] > keyi){right--;}arr[hole] = arr[right];hole = right;while (left < right && arr[left] < keyi){++left;}arr[hole] = arr[left];hole = left;}//left==right时跳出循环,此时的位置为基准值的位置arr[hole] = keyi;return hole;
}void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值--keyiint keyi = _QucikSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}4.2.3 lomuto前后指针法
单趟动态演示:
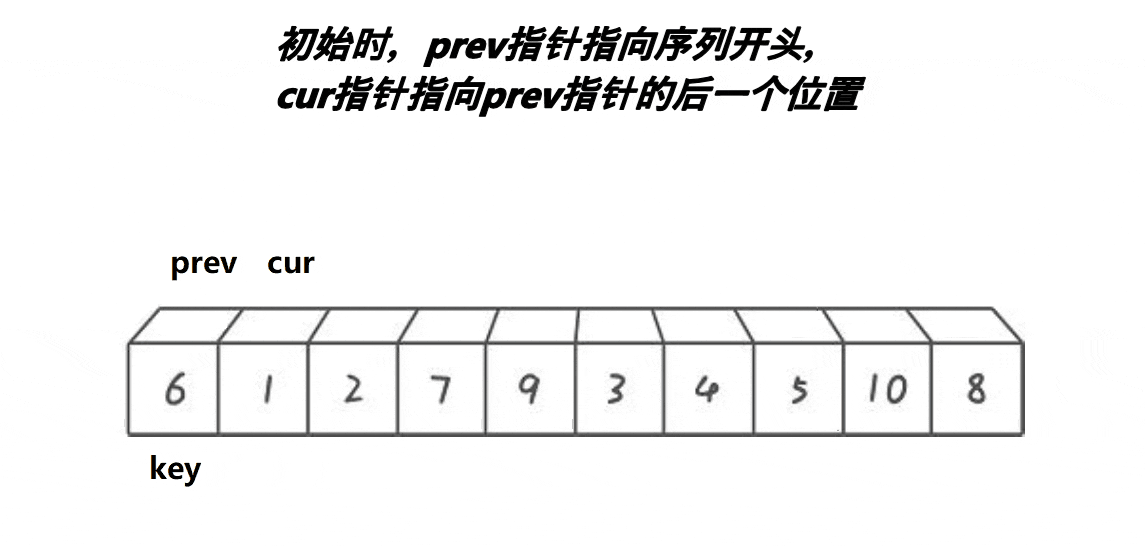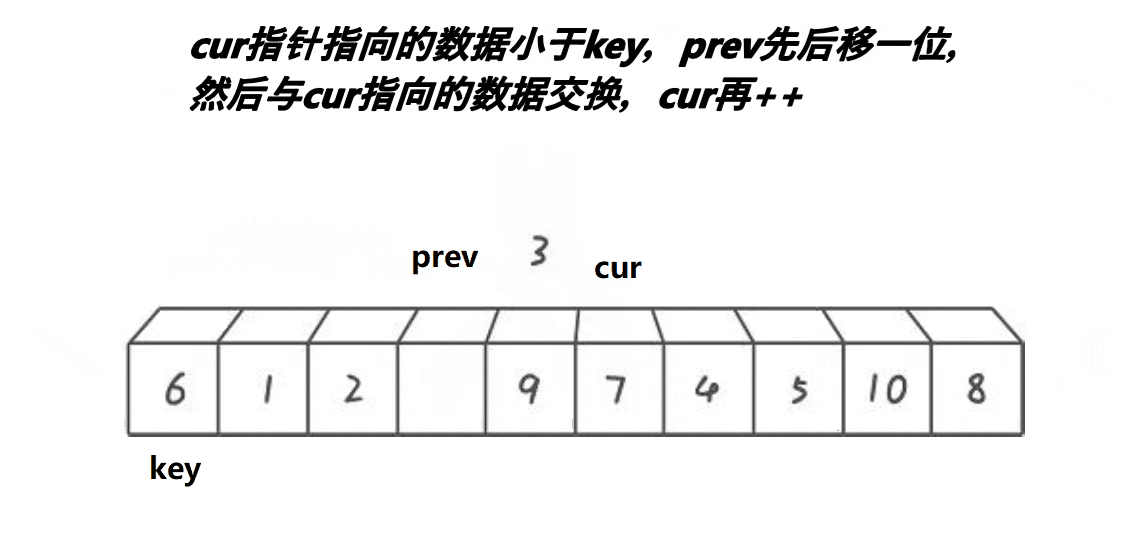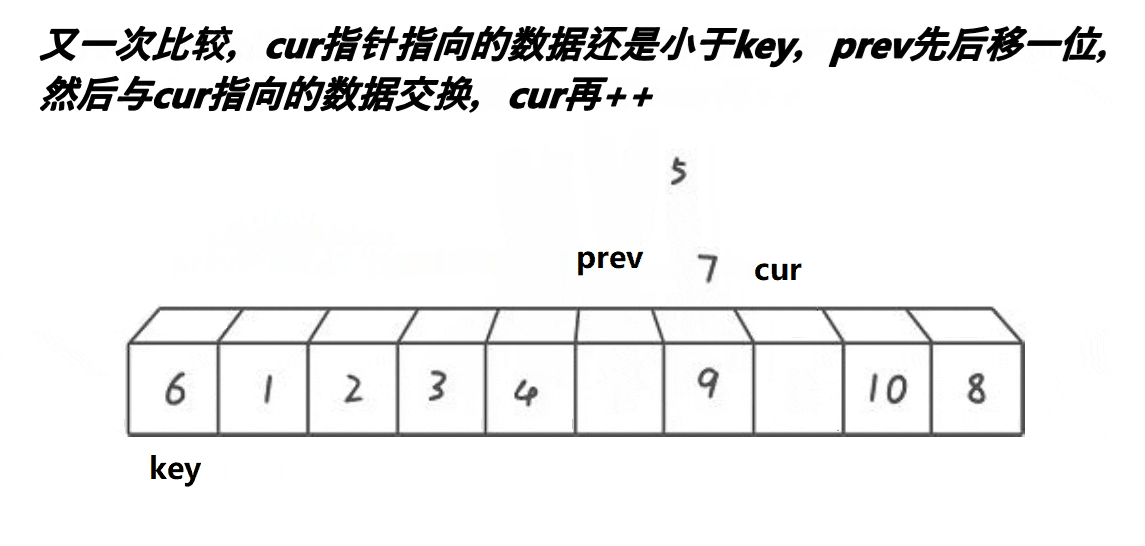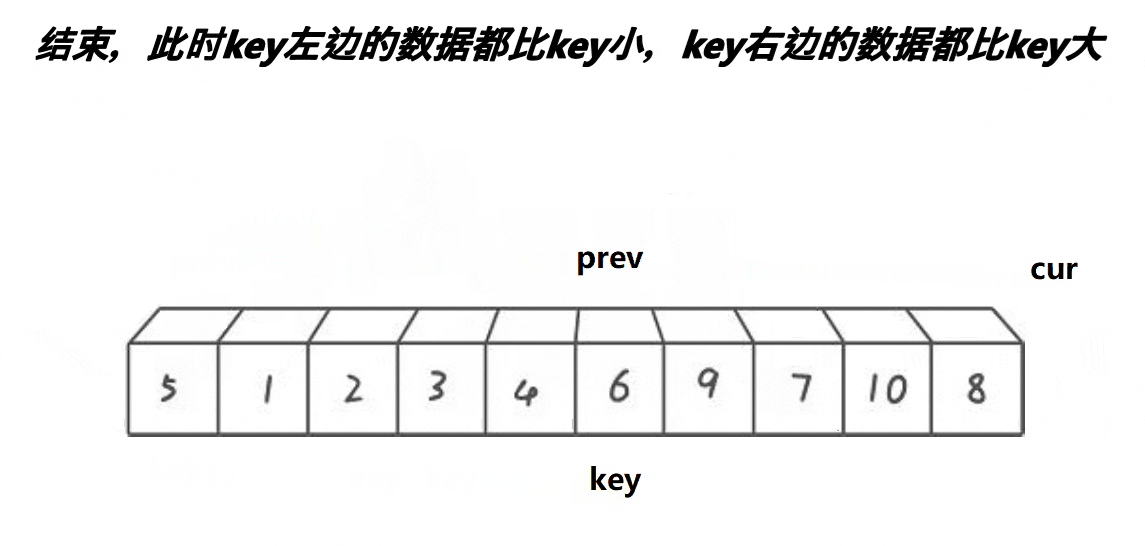
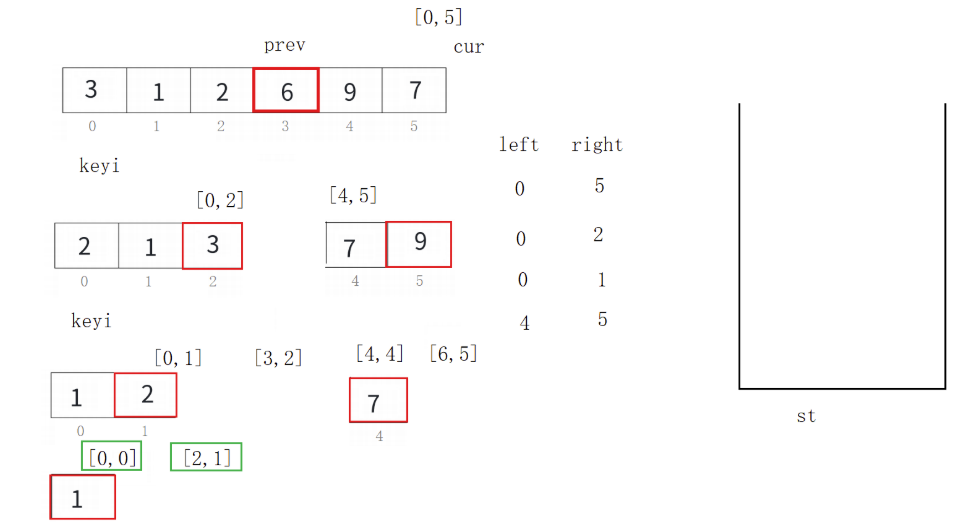
前后指针法的单趟排序的基本步骤如下:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容(prev和cur指向的不是同一个数据时才交换),然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur指针越界,此时将key和prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作。
代码:
int _QucikSort(int* arr, int left, int right)
{int keyi = left;int prev = left, cur = prev + 1;while (cur <= right){if (arr[cur] < arr[keyi] && ++prev != cur){swap(&arr[prev], &arr[cur]);}cur++;}//跳出循环,prev的位置为基准值的位置swap(&arr[prev], &arr[keyi]);return prev;
}
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值--keyiint keyi = _QucikSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}4.2.4 快速排序算法的时间复杂度
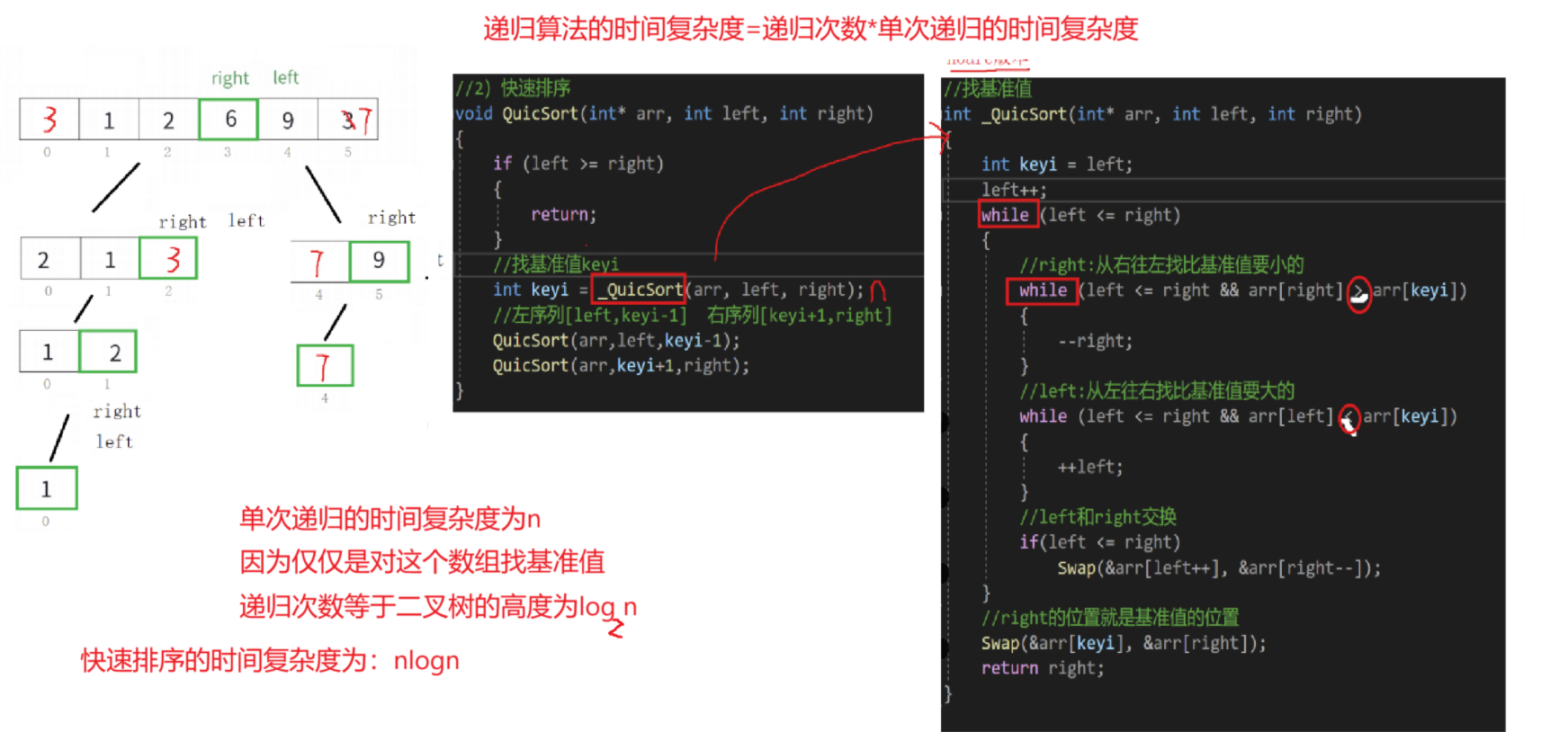
如果快速排序算法的基准值找的不好的情况下,时间复杂度为:n^2

快速排序特性总结:
- 时间复杂度: O(nlogn)
- 空间复杂度: O(logn)
4.3 快速排序--非递归
回顾上面的学习,我们发现快速排序算法的最关键的地方就在于找基准值,先对整个序列找基准值,然后对左右序列找基准值。
不难发现,找基准值的关键所在就在于左右的界限,知道左右的界限,我们就可以根据lomuto双指针法找基准值,那我们怎么存储相应的界限呢?
这就要用到数据结构--栈,让我们一起看一下这个非递归版本是怎么实现的。
快速排序的非递归算法基本思路:
1、先将待排序列的第一个元素的下标和最后一个元素的下标入栈。
2、当栈不为空时,读取栈中的信息(一次读取两个:一个是L,另一个是R),然后调用某一版本的单趟排序,排完后获得了key的下标,然后判断key的左序列和右序列是否还需要排序,若还需要排序,就将相应序列的L和R入栈;若不需排序了(序列只有一个元素或是不存在),就不需要将该序列的信息入栈。
3、反复执行步骤2,直到栈为空为止。
4.3.1 代码
void QuickSort(int* arr, int left, int right)
{ST st;StInit(&st);Stpush(&st, right);Stpush(&st, left);while (!STEmpty(&st)){int begin = STtop(&st);Stpop(&st);int end = STtop(&st);Stpop(&st);int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur){swap(&arr[cur], &arr[prev]);}++cur;}swap(&arr[prev], &arr[keyi]);keyi = prev;//左序列:[begin,keyi-1]//右序列:[keyi+1,end]if (keyi + 1 < end){Stpush(&st, end);Stpush(&st, keyi + 1);}if (begin < keyi - 1){Stpush(&st, keyi - 1);Stpush(&st, begin);}}STDestory(&st);
}4.3.2 代码解释:

时间复杂度: O(nlogn)
