Floyd 判圈算法（龟兔赛跑算法）

是一种用于检测链表或数组中是否存在环（循环依赖）的高效算法。因其只需要 O(1) 的额外空间，被广泛应用于链表环检测、重复数字查找等问题。

1. 算法核心思想

• 快指针（Hare）：每次移动 两步。

• 慢指针（Tortoise）：每次移动 一步。

• 如果存在环，快指针最终会追上慢指针（即两者相遇）。

• 如果快指针到达终点（如 null），则无环。

2. 算法步骤

阶段 1：检测是否有环

1. 初始化 slow 和 fast 指针，都指向起点（如 head 或 nums[0]）。

2. slow 每次移动 1 步，fast 每次移动 2 步。

3. 如果 fast 遇到 null（或数组越界），说明无环。

4. 如果 slow == fast，说明存在环，进入阶段 2。

阶段 2：找到环的入口（关键）

1. 重置 slow 到起点，保持 fast 在相遇点。

2. slow 和 fast 同时每次移动 1 步，直到再次相遇。

3. 相遇点即为环的入口（即重复数字或链表环的起点）。

两个例题（模板题）：

142. 环形链表 II - 力扣（LeetCode）

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {ListNode slow=head;ListNode fast=head;while(fast!=null&&fast.next!=null){slow=slow.next;fast=fast.next.next;if(slow==fast) break;}if(fast==null||fast.next==null) return null;slow=head;while(slow!=fast){slow=slow.next;fast=fast.next;}return slow;}
}

287. 寻找重复数 - 力扣（LeetCode）

eg.

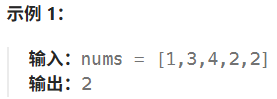
1-0  3-1  4-2  2-3  2-4

0->1->3->2->4->2->4->2->4......，可见，2，4一直循环，存在环。

class Solution {public int findDuplicate(int[] nums) {int slow=nums[0];int fast=nums[0];do{slow=nums[slow];fast=nums[nums[fast]];}while(slow!=fast);slow=nums[0];while(slow!=fast){slow=nums[slow];fast=nums[fast];}return slow;}
}