当前位置：首页 > news >正文

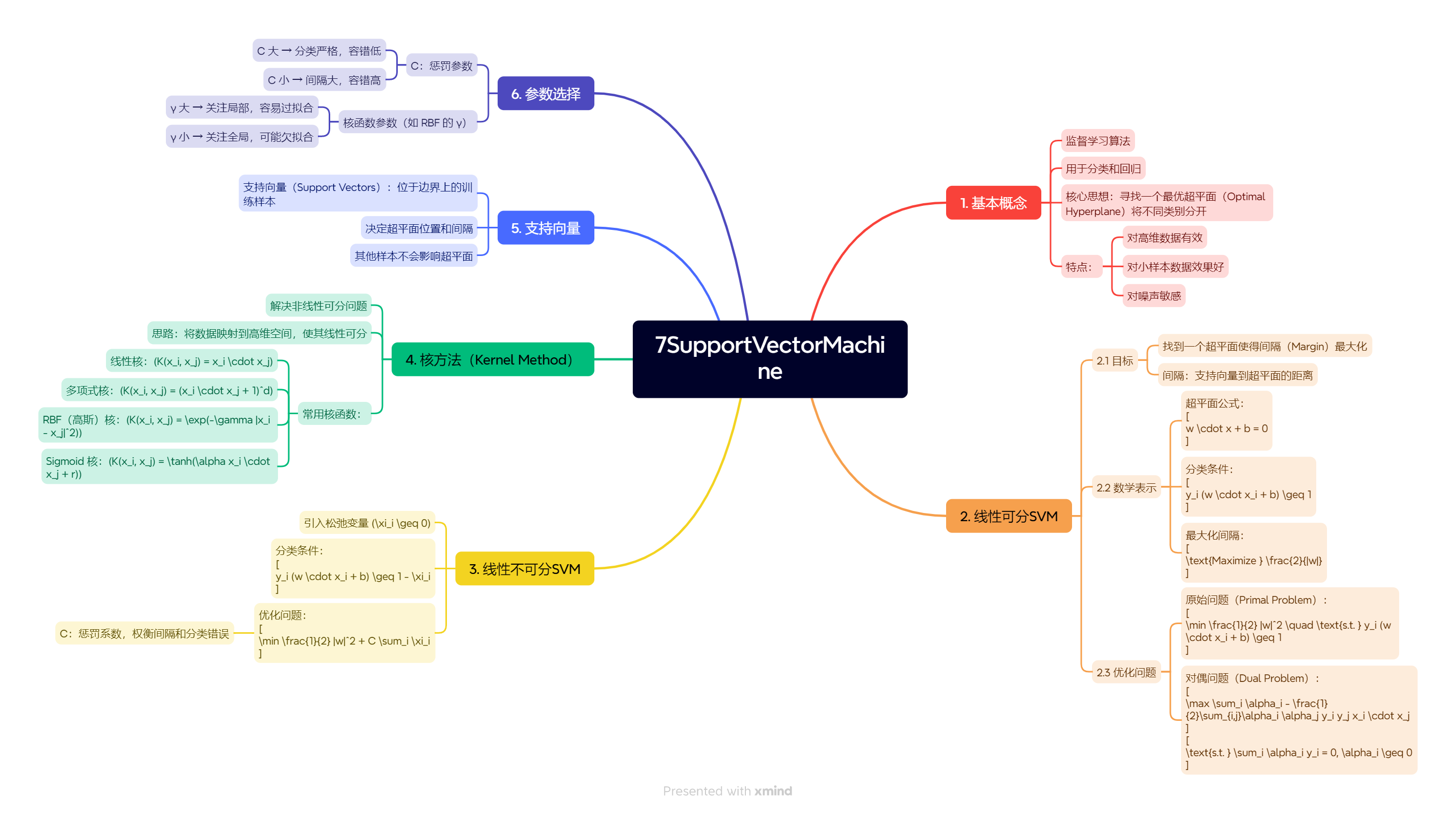
机器学习-支持向量机器（SVM）

news 2025/8/15 15:47:49

在这里插入图片描述

0.1 数字识别

from sklearn.svm import SVC
from sklearn.metrics import silhouette_score
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.feature_extraction import DictVectorizer
from sklearn.cluster import KMeans
from sklearn.metrics import classification_report,roc_curve,roc_auc_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# 封装一个函数用于可视化结果
def visualization(data,c=None,title=None,centers=None):if data.ndim == 1 or data.shape[1] == 1:print("数据维度过低，跳过可视化")returndata = pd.DataFrame(data)pca = PCA(n_components=2)data = pca.fit_transform(data)plt.scatter(data[:, 0], data[:,1],c=c)if centers is not None:plt.scatter(centers[:,0],centers[:,1],c="red",s=100)plt.title(title)plt.show()data = pd.read_csv("../data/shuzi.csv")
X=data.drop(columns="label")
y=data["label"]
X=X.apply(lambda x:x/255,axis=0)
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
AUC = []
for i in [0.75,0.8,0.85,0.9,0.95]:pca = PCA(n_components=i, svd_solver='full')print(i,"：","拷贝")X_train_copy = X_train.copy()X_test_copy = X_test.copy()# 降维print(i,"：","开始降维")X_train_copy =pca.fit_transform(X_train_copy)X_test_copy =pca.transform(X_test_copy)# 训练print(i,"：","开始训练")svc = SVC(C=1,probability=True)svc.fit(X_train_copy,y_train)print(i,"：","开始预测")y_pred = svc.predict(X_test_copy)y_proba = svc.predict_proba(X_test_copy)print(i,"：","开始评估")# fpr, tpr, thresholds = roc_curve(y_test,y_proba[:,1])auc = roc_auc_score(y_test,y_proba,multi_class="ovr")print(i,"评估结果：\n",classification_report(y_test,y_pred))print(i,"：auc：",auc)AUC.append(auc)print(i,"：","可视化：")visualization(y_test,c=y_pred)
# 可视化
fig , axes = plt.subplots(2,1)axes[0].imshow(np.array(X.iloc[0,:]).reshape(28,28))
axes[1].imshow(np.array(X.iloc[1,:]).reshape(28,28))plt.show()

0.2 乳腺癌分类预测

from sklearn.svm import SVC
from sklearn.metrics import silhouette_score
import seaborn as sns
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.feature_extraction import DictVectorizer
from sklearn.cluster import KMeans
from sklearn.metrics import classification_report,roc_curve,roc_auc_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
plt.rcParams['font.sans-serif'] = ['KaiTi']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 绘制决策边界
def plot_boundary(data, estimator, y, pca=None,title=None):"""绘制决策边界和数据点:param data: 预测的数据:param estimator: 训练好的分类器:param y: 数据标签:param pca: PCA对象，用于降维（在函数外已经使用了pca的情况，防止两个pca不一样，输入pca保持降维结果一致）:return: None"""data = np.array(data)if data.ndim == 1 or data.shape[1] == 1:print("维度过低")return # PCA 降维（如果传入pca则直接使用传入的pca）if data.shape[1] > 2:if pca is None:pca = PCA(n_components=2)data_reduced = pca.fit_transform(data)  # 使用不同的变量名else:data_reduced = pca.transform(data)need_inv = True  # 用于标记是否经历过降维（如果降维过在后面需要重新升维，防止与estimator的训练维度不统一）else:data_reduced = data   need_inv = False # 用于标记是否经历过降维（如果降维过在后面需要重新升维，防止与estimator的训练维度不统一）# 基于降维后的数据创建网格min_x, max_x = data_reduced[:,0].min()-1, data_reduced[:,0].max()+1min_y, max_y = data_reduced[:,1].min()-1, data_reduced[:,1].max()+1xx, yy = np.meshgrid(np.arange(min_x, max_x, 0.02),np.arange(min_y, max_y, 0.02))# 转为一维且合并的网格点，每行代表一个网格点，用于后续预测grid_points = np.c_[xx.ravel(), yy.ravel()]# 如果降过维，把网格点升回原始空间再预测if need_inv:grid_original = pca.inverse_transform(grid_points)else:grid_original = grid_points# 预测网格点的类别Z = estimator.predict(grid_original).reshape(xx.shape)# 绘图plt.figure(figsize=(10, 10))plt.contourf(xx, yy, Z, alpha=0.8)plt.scatter(data_reduced[:,0], data_reduced[:,1], c=y, edgecolors='black')plt.title(f"可视化决策边界-{title}")plt.show()
data = pd.read_csv("F:\py_MachineLearning\MachineLearning\MachineLearning\scikit_learn\data\乳腺癌分类.csv")# 可视化
sns.countplot(data,x="diagnosis",
)
plt.title("类别分布")
plt.show()
# 数据集划分
X=data.drop(columns=['Unnamed: 32',"id","diagnosis"])
y = data["diagnosis"]
# 创建字典映射
dict={"B":0,"M":1
}
y = y.map(dict)
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
from sklearn.preprocessing import StandardScaler
# 特征缩放
transfer = StandardScaler()
transfer.fit(X_train)
X_train = pd.DataFrame(transfer.transform(X_train),columns=X.columns)
X_test = pd.DataFrame(transfer.transform(X_test),columns=X.columns)
# 借助决策树挑选特征
from sklearn.tree import DecisionTreeClassifier
DT = DecisionTreeClassifier()
DT.fit(X_train,y_train)
importances = {"feature":X.columns,"importance":DT.feature_importances_
}pd.DataFrame(importances).sort_values(by="importance",ascending=False)#选择radius_worst和concave points_worst
## X_train,X_test=X_train.loc[:,["radius_worst","concave points_worst"]],X_test.loc[:,["radius_worst","concave points_worst"]]svc = SVC() 
svc.fit(X_train,y_train)
y_pred = svc.predict(X_test)
print("classification_report：\n",classification_report(y_test,y_pred))
# 绘制决策边界
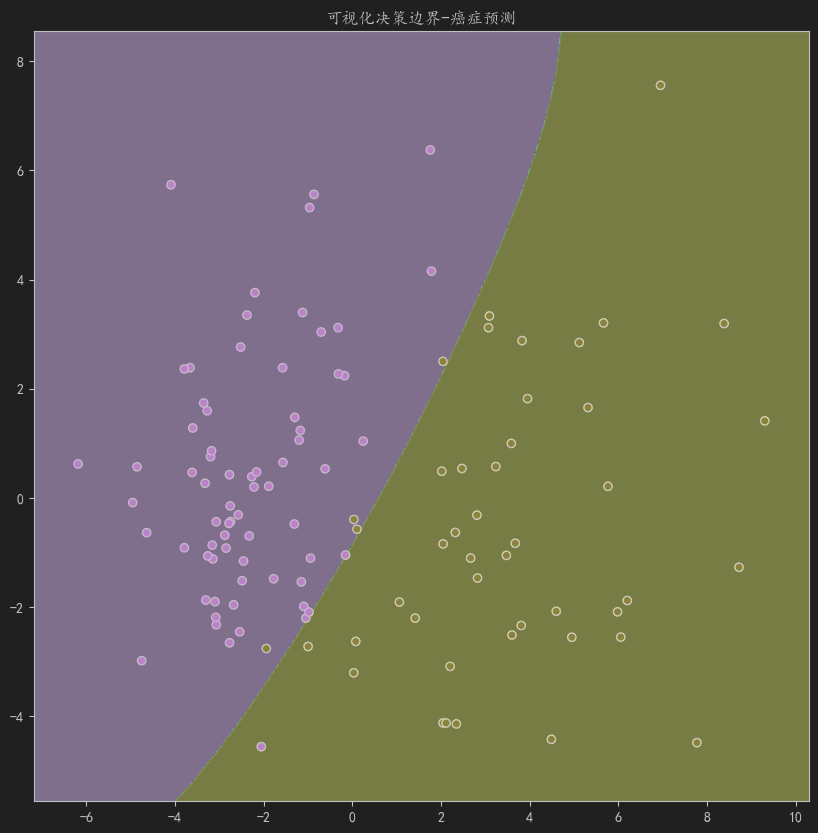
plot_boundary(X_test,svc,y=y_test,title="癌症预测")

结果
在这里插入图片描述

1 相关知识

拉格朗日乘子法：
1 带约束的优化问题

$min_x f_0(x)$

$fi(x)≤0,i=1,...m\text{subject to } f_i(x) \leq 0, i = 1,...m$

$h_i(x) = 0, i = 1,...q$

2 原始转换

$min⁡L(x,λ,v)=f0(x)+∑i=1mλifi(x)+∑i=1qvihi(x)\min L(x, \lambda, v) = f_0(x) + \sum_{i=1}^{m} \lambda_i f_i(x) + \sum_{i=1}^{q} v_i h_i(x)$

2 SVC推导过程

2.1 损失函数的推导

2.1.1 距离的方向

已知决策超平面： $w^TX+b=0$

$w_1x_1+w_2x_2=0$ 可以转化为两个向量相乘 $w_1,w_2)·(x_1,x_2)=0$

此时会发现(w_1,w_2)正好垂直于(x_1,x_2)，这就是法向量，这样就获得了垂直于决策超平面距离的方向 $wT∣∣w∣∣\frac{w^T}{||w|| }$ （除以w的范数是为了保证这个向量的长度=1.只是单纯的方向没有距离信息）

2.1.2 距离的计算

现在只需要在决策超平面上取一个点 $x^{'}$ ，再得到支持向量 $x$ ，计算 $(x−x′)∗wT∣∣w∣∣(x-x')*\frac{w^T}{||w|| }$ 就是 $x, x^{'}$ 在法向量上的距离，也就是支持向量到平面的距离

2.1.3损失函数

现在得到了 $(x−x′)∗wT∣∣w∣∣(x-x')*\frac{w^T}{||w|| }$

因为 $x^{'}$ 取自决策超平面： $w^TX+b=0$ ，所以 $w^Tx'=-b$

所以： $x-x')w=w^Tx-w^Tx'=w^Tx+b$

这样就得到了初步的损失函数： $wTx+b∣∣w∣∣\frac{w^Tx+b}{||w||}$

简化，由于 $y_i$ 和 $wT⋅Φ(xi)+bw^T \cdot \Phi(x_i) + b$ 处于同一侧，符号同号（隐含假设，否则则是分类错误）。所以结果不变，得到： $yi(wT⋅Φ(xi)+b)∣∣w∣∣\frac{y_i \bigl(w^T \cdot \Phi(x_i) + b\bigr)}{||w||}$
( $Φ(xi)\Phi(x_i)$ 表示核函数，表示升维，暂时可继续理解为X)

最后得到：
$arg⁡max⁡w,b{1∣∣w∣∣min⁡i[yi⋅(wT⋅Φ(xi)+b)]}\arg \max_{w,b} \left\{ \frac{1}{||w||} \min_i \left[ y_i \cdot (w^T \cdot \Phi(x_i) + b) \right] \right\}$

2.2 空间缩放

为了进一步简化损失函数

对w和x同乘 $γ\gamma$ 对整个空间进行缩放，使得 $yi⋅(wT⋅Φ(xi)+b)≥1y_i \cdot (w^T \cdot \Phi(x_i) + b) \geq 1$

此时 $min⁡[yi⋅(wT⋅Φ(xi)+b)≥1]\min[y_i \cdot (w^T \cdot \Phi(x_i) + b) \geq 1]$ 就等于1

最后损失函数就成了 $arg⁡max⁡w,b1∣∣w∣∣\arg \max_{w,b}\frac{1}{||w||}$

也产生了一个约束条件： $min⁡[yi⋅(wT⋅Φ(xi)+b)≥1]\min[y_i \cdot (w^T \cdot \Phi(x_i) + b) \geq 1]$
（接下来的推导均处于这个缩放后的空间）

2.3 目标求解

2.3.1 拉格朗日乘子法

现在的目标函数是 $arg⁡max⁡w,b1∣∣w∣∣\arg \max_{w,b}\frac{1}{||w||}$ ，约束条件是 $min⁡[yi⋅(wT⋅Φ(xi)+b)≥1]\min[y_i \cdot (w^T \cdot \Phi(x_i) + b) \geq 1]$

正常来说需要将求解极大值问题转化为求解极小值问题，然后求最优值但此时由于有一个约束条件，可以采用拉格朗日乘子法将约束条件融合进 $f (x)$ ，使其表面上转化为一个无约束问题

通过拉格朗日乘子法得到： $\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^{n} \alpha_i \left( y_i \left( w^T \cdot \Phi(x_i) + b \right) - 1 \right)$ ，约束： $αi>=0\alpha_i>=0$ （这个约束源于拉格朗日乘子法的KKT性质）

( $αi\alpha_i$ ：拉格朗日乘数，负号是因为约束条件被重写为 $−[yi(wT⋅Φ(xi)+b)−1]≤0−[yi(wT⋅Φ(xi)+b)−1]≤0−[yi(wT⋅Φ(xi)+b)−1]≤0−[yi(wT⋅Φ(xi)+b)−1]≤0-[y_i(w^T \cdot \Phi(x_i) + b) - 1] \leq 0−[yi(wT⋅Φ(xi)+b)−1]≤0$ 的形式）

2.3.2 对偶性

由于对偶性质（这个当定理记即可，推导极为复杂）
$min⁡w,bmax⁡αL(w,b,α)→max⁡αmin⁡w,bL(w,b,α)\min_{w,b} \max_{\alpha} L(w,b,\alpha) \to \max_{\alpha} \min_{w,b} L(w,b,\alpha)$

2.3.3 求导*

对w求偏导： $∂L∂w=0⇒w=∑i=1nαiyiΦ(xi)\frac{\partial L}{\partial w} = 0 \Rightarrow w = \sum_{i=1}^{n} \alpha_i y_i \Phi(x_i)$
对b求偏导： $∂L∂b=0⇒0=∑i=1nαiyi\frac{\partial L}{\partial b} = 0 \Rightarrow 0 = \sum_{i=1}^{n} \alpha_i y_i$

代入： $L(w,b,α)=12∣∣w∣∣2−∑i=1nαi(yi(wTΦ(xi)+b)−1)L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^{n} \alpha_i (y_i(w^T \Phi(x_i) + b) - 1)$

其中 $\sum_{i=1}^{n} \alpha_i y_i \Phi(x_i) \quad 0 = \sum_{i=1}^{n} \alpha_i y_i$

$\frac{1}{2}w^T w - w^T \sum_{i=1}^{n} \alpha_i y_i \Phi(x_i) - b\sum_{i=1}^{n} \alpha_i y_i + \sum_{i=1}^{n} \alpha_i$

$\sum_{i=1}^{n} \alpha_i - \frac{1}{2}(\sum_{i=1}^{n} \alpha_i y_i \Phi(x_i))^T \sum_{i=1}^{n} \alpha_i y_i \Phi(x_i) \quad$

$\sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1,j=1}^{n} \alpha_i \alpha_j y_i y_j \Phi^T(x_i)\Phi(x_j)$

继续对α求极大值： $max⁡α∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj(Φ(xi)⋅Φ(xj))\max_{\alpha} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (\Phi(x_i) \cdot \Phi(x_j))$

条件： $∑i=1nαiyi=0\sum_{i=1}^{n} \alpha_i y_i = 0$ 、 $αi≥0\alpha_i \geq 0$

极大值转换成求极小值： $min⁡α12∑i=1n∑j=1nαiαjyiyj(Φ(xi)⋅Φ(xj))−∑i=1nαi\min_{\alpha} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (\Phi(x_i) \cdot \Phi(x_j)) - \sum_{i=1}^{n} \alpha_i$

条件： $∑i=1nαiyi=0\sum_{i=1}^{n} \alpha_i y_i = 0$ 、 $αi≥0\alpha_i \geq 0$

2.4松弛因子

加入松弛因子成为软间隔
$min⁡12∣∣w∣∣2+C∑i=1nξi\min \frac{1}{2} ||w||^2 + C \sum_{i=1}^{n} \xi_i$
约束变成了 $\alpha_i - \mu_i = 0$ 和 $μi≥0\mu_i \geq 0$

通过与硬间隔一样的求解方式最后得到解
$min⁡α12∑i=1n∑j=1nαiαjyiyj(xi⋅xj)−∑i=1nαi\min_{\alpha} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{n} \alpha_i$
约束：
$∑i=1nαiyi=0\sum_{i=1}^{n} \alpha_i y_i = 0$ 、 $\leq \alpha_i \leq C$

3 SVC api

(基于SVM的分类)
SVC(C=1.0,
gamma=‘scale’,
random_state=None,
)

C ： # 正则化参数，控制分类边界的平滑程度。C值越大对误分类惩罚越强，可能导致过拟合；C值较小则允许更多误分类，泛化能力更强但可能欠拟合
gamma：# 核函数系数，可选’scale’(1/(n_features*X.var()))、‘auto’(1/n_features)或具体数值。影响数据映射到高维空间的分布

代码示例

from sklearn.datasets import load_iris
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_reportiris = load_iris()
data= pd.DataFrame(iris.data, columns=iris.feature_names)
data["target"] = iris.target
X = data.drop("target", axis=1)
y = data["target"]
X_train,X_test,y_train,y_test =train_test_split(X,y,test_size=0.2)transfer = StandardScaler()
X_train = transfer.fit_transform(X_train)
X_test = transfer.transform(X_test)svc = SVC(kernel='rbf')
svc.fit(X_train,y_train)
y_pred = svc.predict(X_test)print(classification_report(y_test, y_pred))

4 SVR

4.1 原理

目的：
SVR也是拟合一个函数 $y = w x + b$ 这一点有些类似于线性回归

2. 核心概念

1 ε-不敏感区间
如果 |f(x_i) - y_i| ≤ ε，则认为预测是“足够好”，不计入损失

2 支持向量
只有落在 ε 区间之外的数据点才会对模型产生影响，这些点称为支持向量

3. 损失函数
SVR 的损失函数（ε-insensitive loss）：

$L_\epsilon(y, f(x)) = \begin{cases} 0, & \text{if } |y - f(x)| \le \epsilon \\ |y - f(x)| - \epsilon, & \text{if } |y - f(x)| > \epsilon \end{cases}$

(只有预测值超过 ε 的误差才会被惩罚)

4. 优化目标
最小化：
$1/2 ||w||^2 + C ∑_i (ξ_i + ξ_i^*)$

ξ_i, ξ_i^*：松弛变量，度量超出 ε 的误差
C：控制对超出误差的惩罚程度
可通过对偶问题使用核函数处理非线性情况

核方法
与SVC一样

理解
除了支持向量（线性回归的误差的样本参与计算，SVR的误差只有在 ε 区间之外的数据点才参与计算）、核方法和松弛变量（线性回归并没有这种内嵌的正则化方式）等区别。SVR就是使用的线性回归那套损失函数，只是SVR根据自身的思想改了一点，且最终有一个 $∣∣ w ∣∣$ 距离不是像线性回归一样的均方误差而是通过SVM的计算 $∣∣ w ∣∣$ 的方式来计算的。也就是说SVR就是基于支持向量思想对线性回归的升级

4.2 api

（基于SVM的回归）
from sklearn.svm import SVR

SVR(kernel=‘rbf’, C=100, gamma=0.1, epsilon=0.1)

常用参数‌：
C：正则化参数。C的值越大，模型会尽可能减小训练误差，这可能导致过拟合。C的值越小，模型会尽可能平坦，这可能导致欠拟合。
epsilon：SVR中的ε-不敏感损失函数参数。它指定了SVR中函数f与真实值y之间允许的最大偏差。在这个间隔内的样本点被忽略，只有间隔边缘上的样本点才被用于计算损失。
kernel：指定算法中使用的核函数类型。常见的核函数有线性核（‘linear’）、多项式核（‘poly’）、径向基函数核（‘rbf’）等。
degree和gamma参数与SVC中的含义相同。

‌常用方法‌：**
fit(X, y)：训练模型。
predict(X)：使用训练好的模型进行预测。
score(X, y)：返回给定测试数据和标签的R^2分数，也称为确定系数。它是回归模型拟合优度的一种度量。最好的可能分数是1.0，它可能小于1.0（因为模型的误差可能比随机误差大）。

代码示例

from sklearn.svm import SVR
from sklearn.metrics import root_mean_squared_error
import numpy as np 
import matplotlib.pyplot as plt
X=np.sort(5*np.random.rand(100,1),axis=0)#100个0-5之间的随机数,并按列排序
y = np.sin(X).ravel()+np.random.rand(100)*0.3svr = SVR(C=100,gamma=0.1) # 核函数参数 影响决策边界的形状)
svr.fit(X,y)X_test = np.linspace(0,5,100)
X_test = X_test.reshape(-1,1)
pred =svr.predict(X_test)plt.scatter(X,y)
plt.plot(X_test,pred,c ="red")
plt.show()
root_mean_squared_error(y,pred)# svr = SVR(kernel='rbf')