高并发内存池 性能瓶颈分析与基数树优化(9)

---

前言

  到了最后一篇喽，嘻嘻！
  终于是要告一段落了，接下来我们将学什么呢，再说吧，可能得把Linux的一些内容给补完

---

一、性能瓶颈分析

操作步骤及其环境配置

  我们的代码此时与 malloc 之间还是有差距的，所以现在我们来分析一下我们的代码

  这里就要借助 VS 的一些神奇妙妙功能了，首先先确保在 Debug 环境下运行，依次点击“调试→性能探查器”进行性能分析

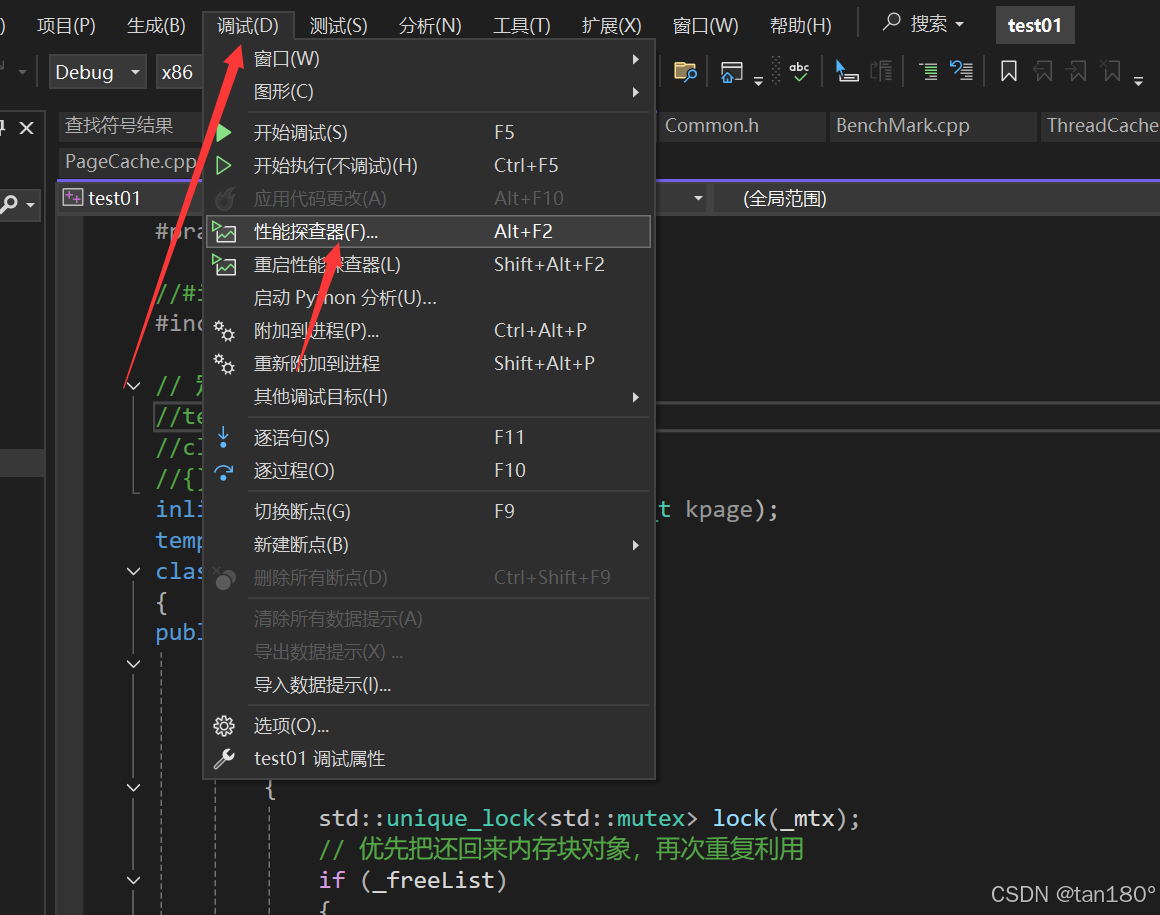
  同时我们屏蔽一下 malloc / free 的 BenchMark 函数，而是就对我们自己的 内存池 进行分析

int main()
{size_t n = 10000;cout << "==========================================================" << endl;BenchmarkConcurrentMalloc(n, 4, 10);cout << endl << endl;//BenchmarkMalloc(n, 4, 10);cout << "==========================================================" << endl;return 0;
}

  接下来我们点击勾选“检测”，再点击“开始”进行

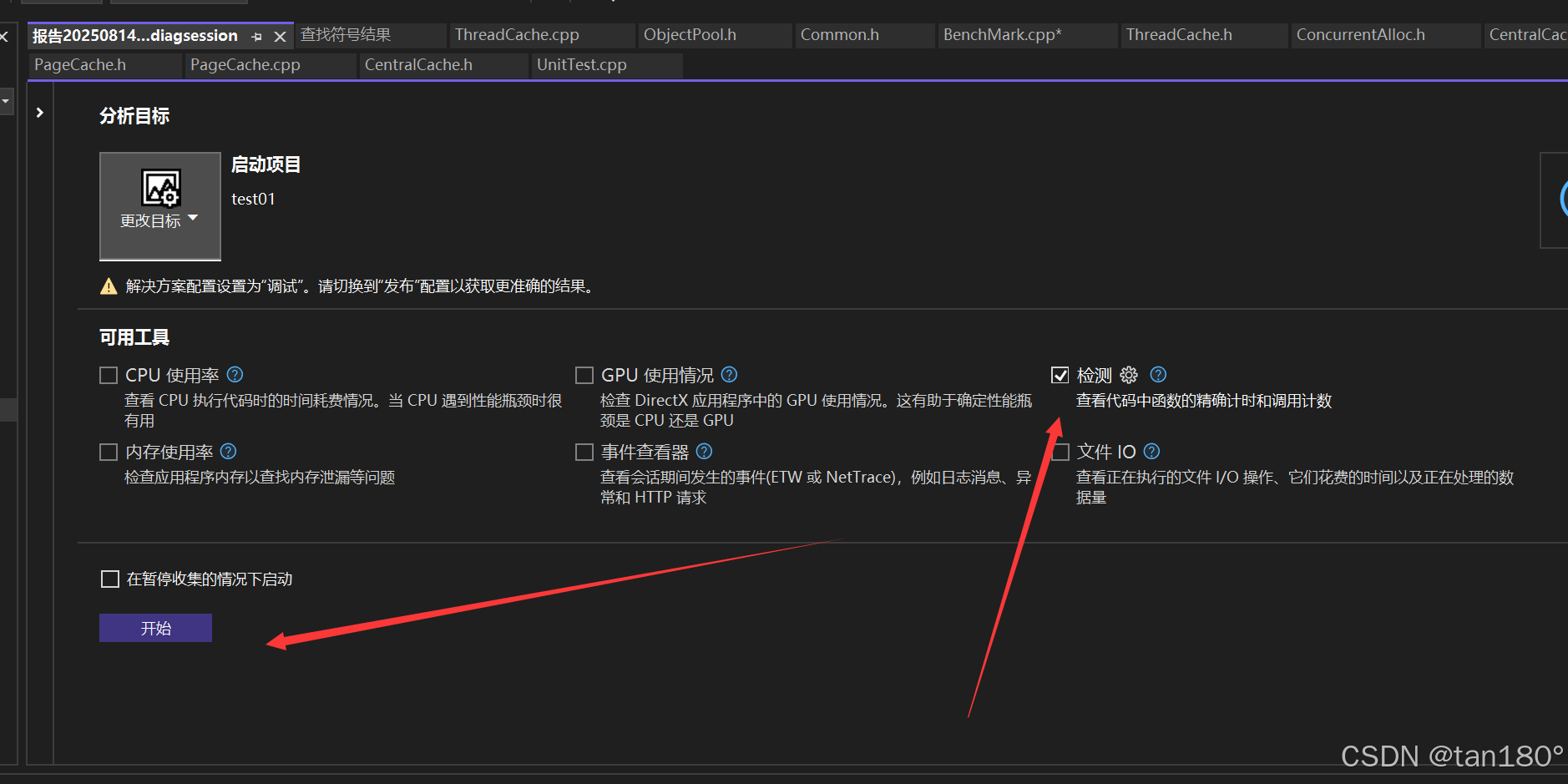
  接着会弹出这个页面，说明此时此刻你没配置，当然了，我一开始也没有

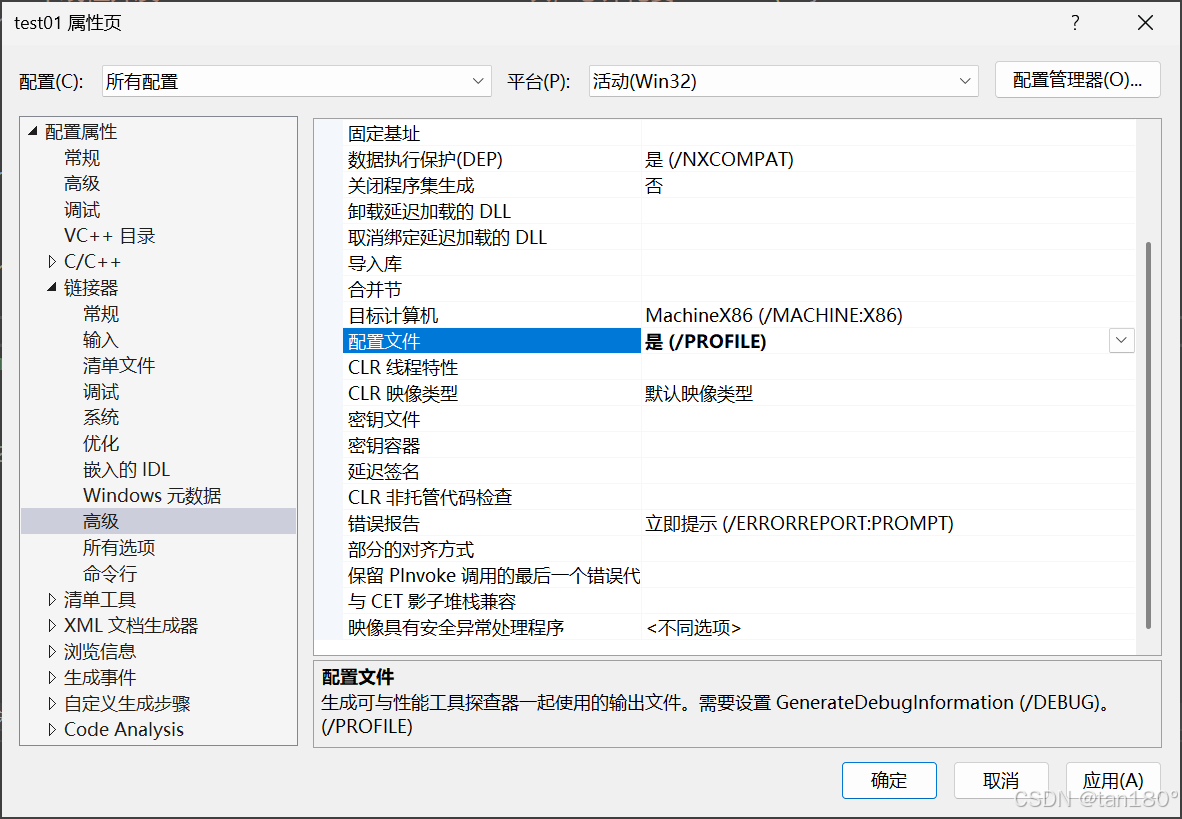
  那具体要怎么配置呢？直接就来个讲解吧！先右键项目名称，然后再点击属性

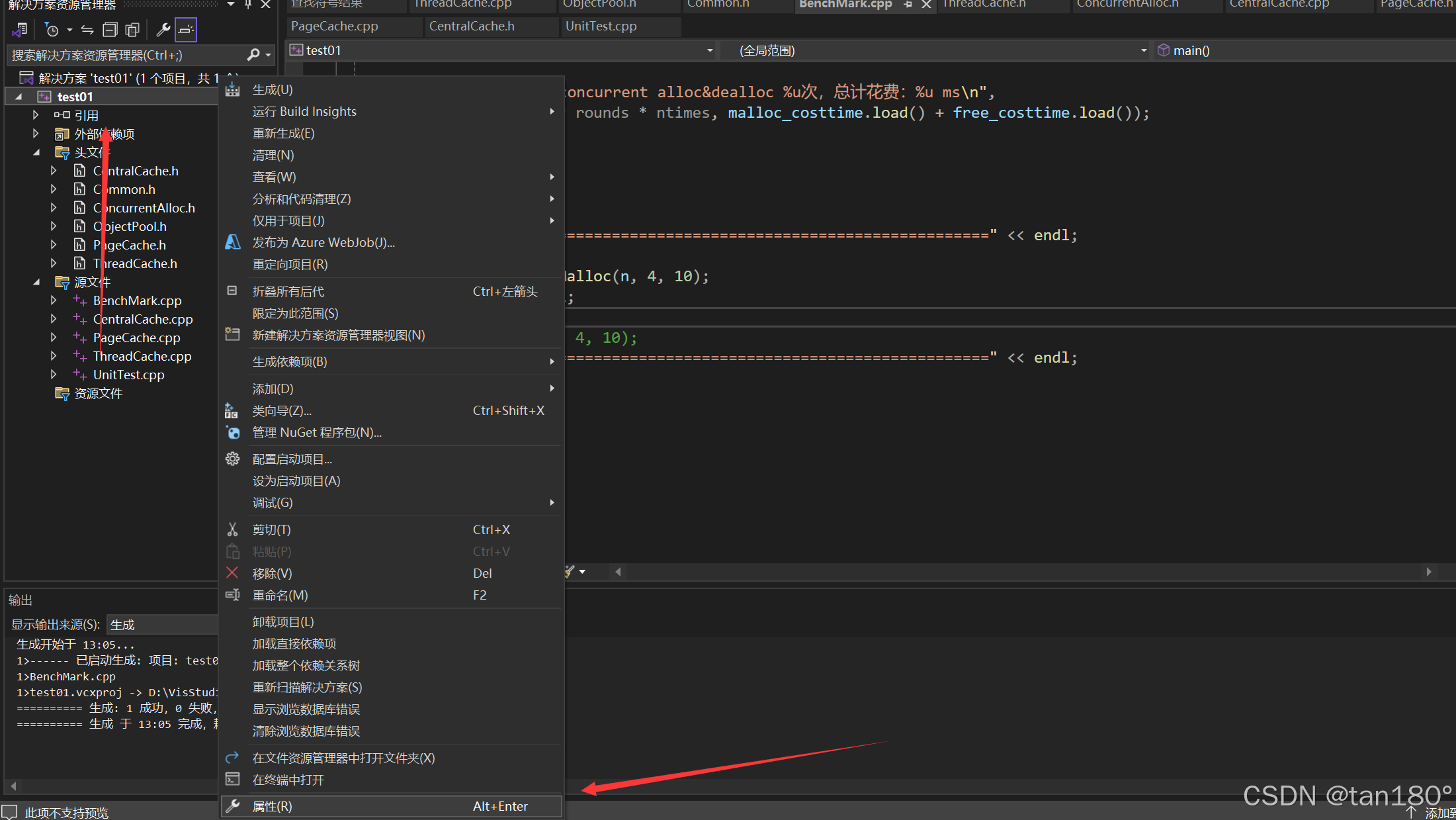
  然后再依次 点击配置属性 -> 点击链接器 -> 点击高级 -> 将配置文件设置为是(/PROFILE)

    好了这下你就配置好了，那么我们接下来继续启动性能分析器，看看到底怎么个说法

    接下来就静静等待结果就好了

分析性能瓶颈

    通过分析结果可以看到，ConcurrentAlloc 和 ConcurrentFree 这两个函数占用了接近60%的时间

    接着将视图修改为调用方/被调用方，这样看起来更加直观

    点击占用时间最多的 Allocate ，再点击占用时间最多的 FetchFromCentralCache ，再点击占用时间最多的 FetchRangeObj ，再点击占用时间最多的 GetOneSpan ，再点击进去就是 lock函数 占用最多时间了，事实上 ConcurrentAlloc 也同样如此，就是因为锁竞争导致了浪费那么多的时间

    针对此瓶颈，我们想到了使用基数树进行性能优化

二、基数树优化

  基数树实际上就是一个分层的哈希表，根据所分层数不同可分为单层基数树、二层基数树、三层基数树等。

  或者我们不如先来想想为什么要加锁，无非就是因为STL底层不保证线程安全，因为 unordered_map的底层数据结构是红黑树，在访问映射关系的时候如果另一个线程进行添加映射的时候，可能由于插入或者旋转导致读取线程发生错误，而基数树就可以完全避免这个问题，至于N层只是说根据不同环境下的不同选择

单层基数树

    因为我是在 32位 环境下写的，所以我将选择这个基数树，当然原理都是一样的，如果你是64位环境下，那我还是建议你用三层基数树吧

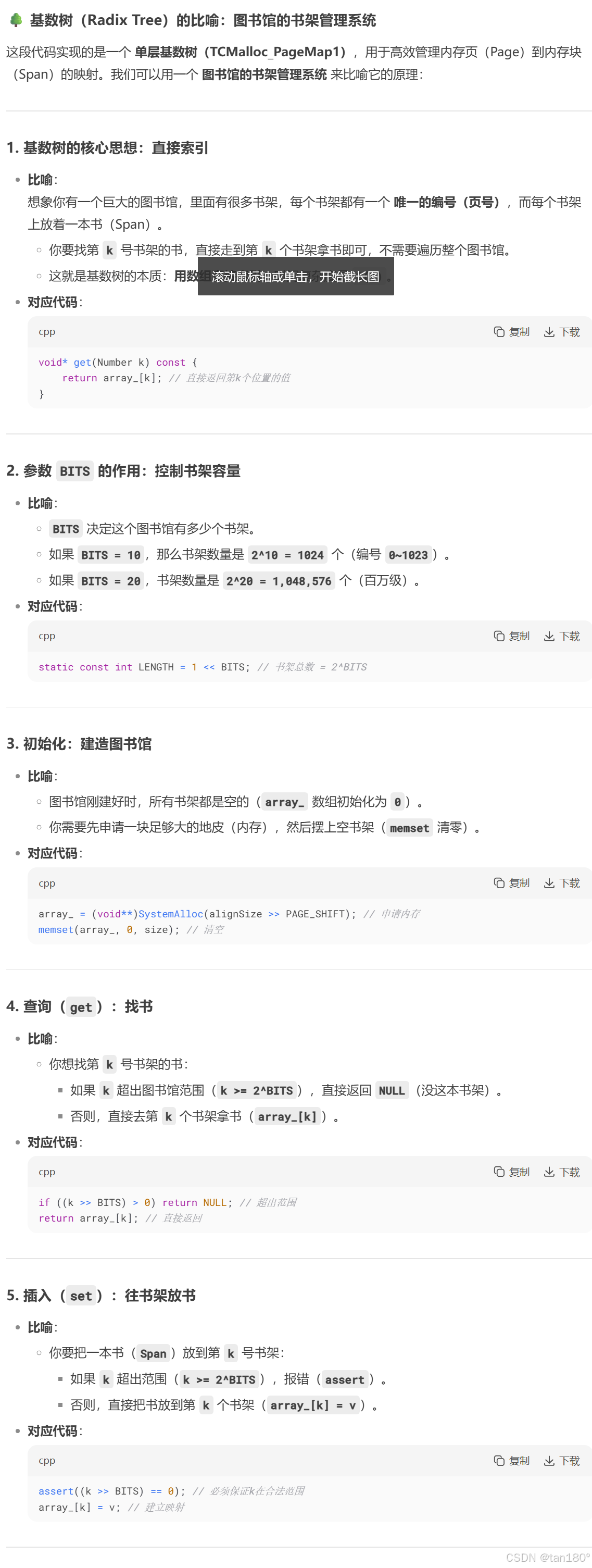
    单层基数树实际采用的就是直接定址法，每一个页号对应 span 的地址就存储数组中在以该页号为下标的位置。

    最坏的情况下我们需要建立所有页号与其 span 之间的映射关系，因此这个数组中元素个数应该与页号的数目相同，数组中每个位置存储的就是对应 span 的指针

//单层基数树
template <int BITS>
class TCMalloc_PageMap1
{
public:typedef uintptr_t Number;explicit TCMalloc_PageMap1(){size_t size = sizeof(void*) << BITS; //需要开辟数组的大小size_t alignSize = SizeClass::_RoundUp(size, 1 << PAGE_SHIFT); //按页对齐后的大小array_ = (void**)SystemAlloc(alignSize >> PAGE_SHIFT); //向堆申请空间memset(array_, 0, size); //对申请到的内存进行清理}void* get(Number k) const{if ((k >> BITS) > 0) //k的范围不在[0, 2^BITS-1]{return NULL;}return array_[k]; //返回该页号对应的span}void set(Number k, void* v){assert((k >> BITS) == 0); //k的范围必须在[0, 2^BITS-1]array_[k] = v; //建立映射}
private:void** array_; //存储映射关系的数组static const int LENGTH = 1 << BITS; //页的数目
};

    当我们需要建立映射时就调用set函数，需要读取映射关系时，就调用get函数

    比如32位平台下，以一页大小为8K为例，此时页的数目就是2 ^ 32 ÷ 2 ^ 13 = 2 ^ 19 ，因此存储页号最多需要19个比特位，此时传入非类型模板参数的值就是32 − 13 = 19。由于32位平台下指针的大小是4字节，因此该数组的大小就是2 ^ 19 × 4 = 2 ^ 21 = 2 M ，内存消耗不大，是可行的。但如果是在64位平台下，此时该数组的大小是2 ^ 51 × 8 = 2 ^ 54 = 2 ^ 24 G ，这显然是不可行的，实际上对于64位的平台，我们需要使用三层基数树

    其实又是时间换空间的思想，这真是一个经久不衰的结论

下面是DS大人给出的结合比喻的解析

二层基数树

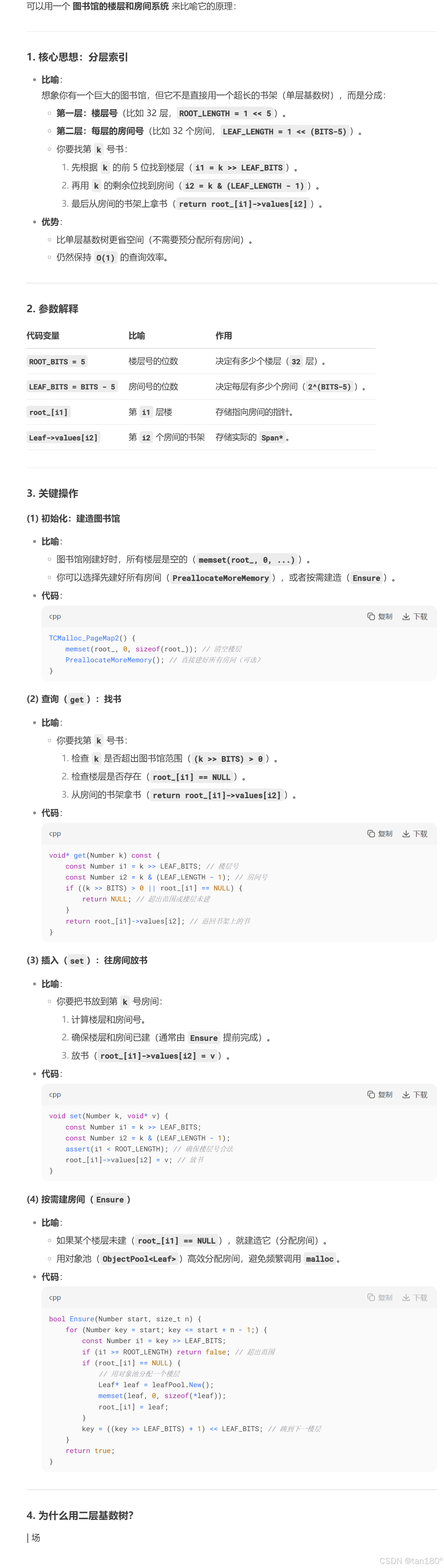
    这里还是以 32位 平台下，一页的大小为 8K 为例来说明，此时存储页号最多需要 19个 比特位。而二层基数树实际上就是把这 19个 比特位分为两次进行映射。

    比如用前5个比特位在基数树的第一层进行映射，映射后得到对应的第二层，然后用剩下的比特位在基数树的第二层进行映射，映射后最终得到该页号对应的span指针。

    在二层基数树中，第一层的数组占用 2 ^ 5 × 4 = 2 ^ 7 Byte 空间，第二层的数组最多占用 2 ^ 5 × 2 ^ 14 × 4 = 2 ^ 21 = 2 M 。二层基数树相比一层基数树的好处就是，一层基数树必须一开始就把 2 M 的数组开辟出来，而二层基数树一开始时只需将第一层的数组开辟出来，当需要进行某一页号映射时再开辟对应的第二层的数组就行了

//二层基数树
template <int BITS>
class TCMalloc_PageMap2
{
private:static const int ROOT_BITS = 5;                //第一层对应页号的前5个比特位static const int ROOT_LENGTH = 1 << ROOT_BITS; //第一层存储元素的个数static const int LEAF_BITS = BITS - ROOT_BITS; //第二层对应页号的其余比特位static const int LEAF_LENGTH = 1 << LEAF_BITS; //第二层存储元素的个数//第一层数组中存储的元素类型struct Leaf{void* values[LEAF_LENGTH];};Leaf* root_[ROOT_LENGTH]; //第一层数组
public:typedef uintptr_t Number;explicit TCMalloc_PageMap2(){memset(root_, 0, sizeof(root_)); //将第一层的空间进行清理PreallocateMoreMemory(); //直接将第二层全部开辟}void* get(Number k) const{const Number i1 = k >> LEAF_BITS;        //第一层对应的下标const Number i2 = k & (LEAF_LENGTH - 1); //第二层对应的下标if ((k >> BITS) > 0 || root_[i1] == NULL) //页号值不在范围或没有建立过映射{return NULL;}return root_[i1]->values[i2]; //返回该页号对应span的指针}void set(Number k, void* v){const Number i1 = k >> LEAF_BITS;        //第一层对应的下标const Number i2 = k & (LEAF_LENGTH - 1); //第二层对应的下标assert(i1 < ROOT_LENGTH);root_[i1]->values[i2] = v; //建立该页号与对应span的映射}//确保映射[start,start_n-1]页号的空间是开辟好了的bool Ensure(Number start, size_t n){for (Number key = start; key <= start + n - 1;){const Number i1 = key >> LEAF_BITS;if (i1 >= ROOT_LENGTH) //页号超出范围return false;if (root_[i1] == NULL) //第一层i1下标指向的空间未开辟{//开辟对应空间static ObjectPool<Leaf> leafPool;Leaf* leaf = (Leaf*)leafPool.New();memset(leaf, 0, sizeof(*leaf));root_[i1] = leaf;}key = ((key >> LEAF_BITS) + 1) << LEAF_BITS; //继续后续检查}return true;}void PreallocateMoreMemory(){Ensure(0, 1 << BITS); //将第二层的空间全部开辟好}
};

    下面又是DS大人给出的解释

三层基数树

    原理图如下，其实还是很好看的

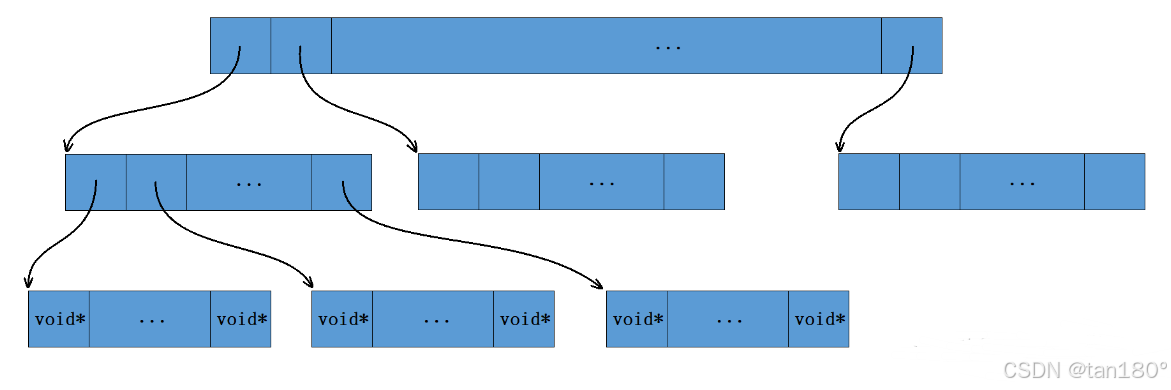
//三层基数树
template <int BITS>
class TCMalloc_PageMap3
{
private:static const int INTERIOR_BITS = (BITS + 2) / 3;       //第一、二层对应页号的比特位个数static const int INTERIOR_LENGTH = 1 << INTERIOR_BITS; //第一、二层存储元素的个数static const int LEAF_BITS = BITS - 2 * INTERIOR_BITS; //第三层对应页号的比特位个数static const int LEAF_LENGTH = 1 << LEAF_BITS;         //第三层存储元素的个数struct Node{Node* ptrs[INTERIOR_LENGTH];};struct Leaf{void* values[LEAF_LENGTH];};Node* NewNode(){static ObjectPool<Node> nodePool;Node* result = nodePool.New();if (result != NULL){memset(result, 0, sizeof(*result));}return result;}Node* root_;
public:typedef uintptr_t Number;explicit TCMalloc_PageMap3(){root_ = NewNode();}void* get(Number k) const{const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标const Number i3 = k & (LEAF_LENGTH - 1);                    //第三层对应的下标//页号超出范围，或映射该页号的空间未开辟if ((k >> BITS) > 0 || root_->ptrs[i1] == NULL || root_->ptrs[i1]->ptrs[i2] == NULL){return NULL;}return reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3]; //返回该页号对应span的指针}void set(Number k, void* v){assert(k >> BITS == 0);const Number i1 = k >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标const Number i2 = (k >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标const Number i3 = k & (LEAF_LENGTH - 1);                    //第三层对应的下标Ensure(k, 1); //确保映射第k页页号的空间是开辟好了的reinterpret_cast<Leaf*>(root_->ptrs[i1]->ptrs[i2])->values[i3] = v; //建立该页号与对应span的映射}//确保映射[start,start+n-1]页号的空间是开辟好了的bool Ensure(Number start, size_t n){for (Number key = start; key <= start + n - 1;){const Number i1 = key >> (LEAF_BITS + INTERIOR_BITS);         //第一层对应的下标const Number i2 = (key >> LEAF_BITS) & (INTERIOR_LENGTH - 1); //第二层对应的下标if (i1 >= INTERIOR_LENGTH || i2 >= INTERIOR_LENGTH) //下标值超出范围return false;if (root_->ptrs[i1] == NULL) //第一层i1下标指向的空间未开辟{//开辟对应空间Node* n = NewNode();if (n == NULL) return false;root_->ptrs[i1] = n;}if (root_->ptrs[i1]->ptrs[i2] == NULL) //第二层i2下标指向的空间未开辟{//开辟对应空间static ObjectPool<Leaf> leafPool;Leaf* leaf = leafPool.New();if (leaf == NULL) return false;memset(leaf, 0, sizeof(*leaf));root_->ptrs[i1]->ptrs[i2] = reinterpret_cast<Node*>(leaf);}key = ((key >> LEAF_BITS) + 1) << LEAF_BITS; //继续后续检查}return true;}void PreallocateMoreMemory(){}
};

    当然要注意的是此时只有当要建立某一页号的映射关系时，再开辟对应的数组空间，而没有建立映射的页号就可以不用开辟其对应的数组空间，此时就能在一定程度上节省内存空间

三、使用基数树来优化代码

    此时将 PageCache类 当中的 unorder_map 用 基数树 进行替换即可，由于当前是 32位 平台，因此这里随便用几层基数树都可以

// 单例模式
class PageCache
{
public://...
private://std::unordered_map<PAGE_ID, Span*> _idSpanMap;TCMalloc_PageMap1<32 - PAGE_SHIFT> _idSpanMap;
};

    当我们需要建立页号与span的映射时，就调用基数树当中的set函数。

_idSpanMap.set(span->_pageId, span);

    而当我们需要读取某一页号对应的span时，就调用基数树当中的get函数

Span* ret = (Span*)_idSpanMap.get(id);

    并且现在 PageCache类 向外提供的，用于读取映射关系的 MapObjectToSpan函数 内部就不需要加锁了（因为基数树空间固定，支持并发访问）

//获取从对象到span的映射
Span* PageCache::MapObjectToSpan(void* obj)
{PAGE_ID id = (PAGE_ID)obj >> PAGE_SHIFT; //页号Span* ret = (Span*)_idSpanMap.get(id);assert(ret != nullptr);return ret;
}

    最后看看效果吧，下面是添加了基数树优化后的对比，依次是固定内存大小、不固定内存大小

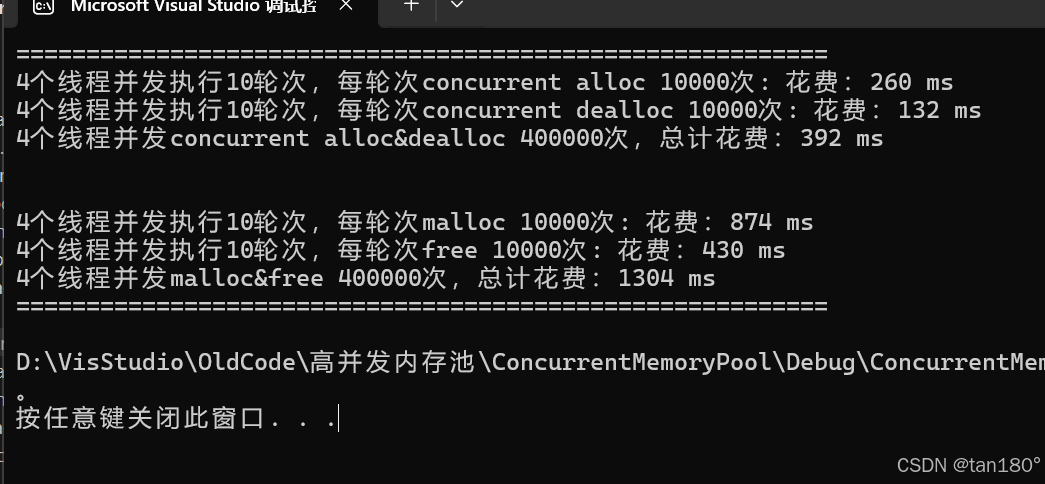
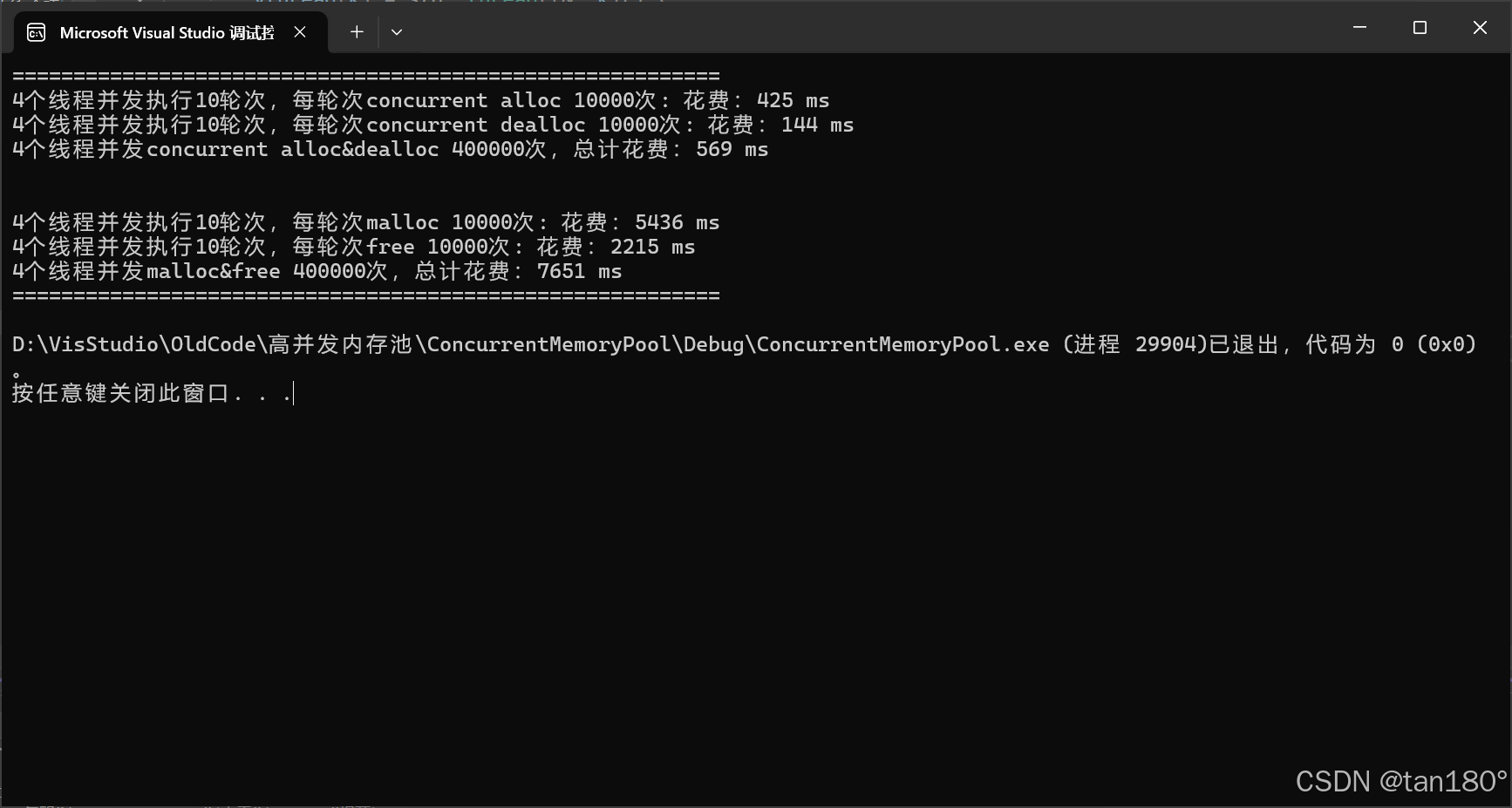
    可以看到在不固定内存大小的前提下，由于 central cache 的桶锁机制，对比差距更大了

---

总结

  代码的世界里，没有“完美”，只有“不断迭代”，这个内存池是我的第一个项目，也是第一个孩子，过去学到的“锁优化”“内存对齐”“数据结构”不再是抽象概念，而是解决实际问题的工具，C++本身就与性能优化及其相关，通过这个项目也是领悟到了锁的魅力，真切感受到了工程能力的成长

  下一步可以怎么继续加深学习呢，或许可以尝试将内存池嵌入实际应用（如HTTP服务器）？不过那是之后的事了呢，但是我现在需要休息一下~