二进制与进制转换

目录

一、进制

1、进制的基本概念

2、十进制系统

3、二进制系统

二、进制转换方法

1、二进制转十进制

2、十进制转二进制

3、二进制与八进制/十六进制转换

二进制转八进制：

二进制转十六进制：

三、负数的表示：原码、反码和补码

1、基本概念

2、示例

3、补码的重要性

四、总结

---

一、进制

1、进制的基本概念

        我们经常听到的2进制、8进制、10进制、16进制等都是数值的不同表示形式。它们的主要区别在于"基数"不同：

• 10进制：基数为10，使用数字0-9

• 2进制：基数为2，使用数字0-1

• 8进制：基数为8，使用数字0-7

• 16进制：基数为16，使用数字0-9及A-F

例如，数值15在不同进制下的表示：

• 2进制：1111

• 8进制：17（通常写作017）

• 10进制：15

• 16进制：F（通常写作0xF）

2、十进制系统

十进制是我们日常生活中最常用的计数系统：

• 采用"满十进一"的规则

• 每一位都是0-9的数字

• 每一位都有对应的位权（10的幂次方）

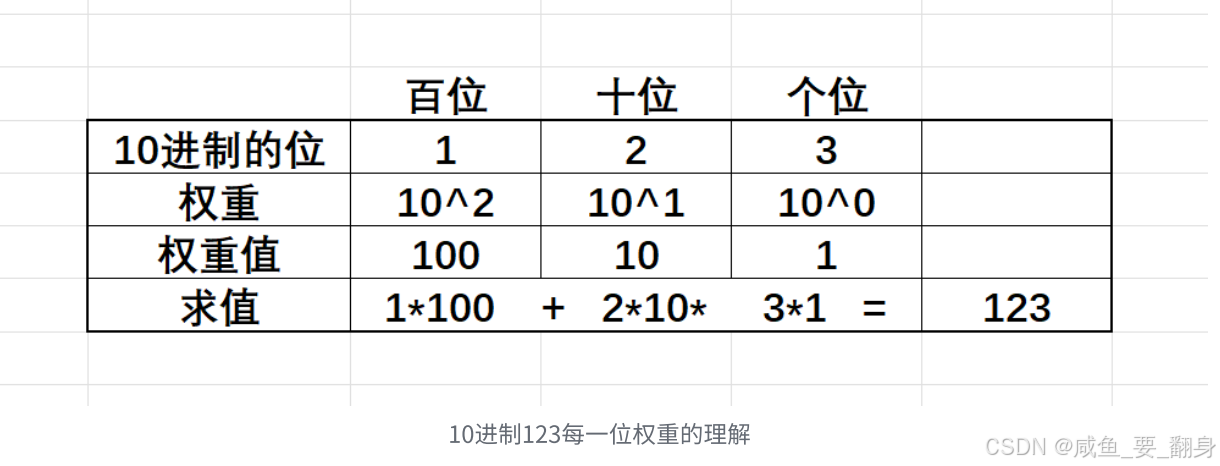
例如，十进制数123表示：1×10² + 2×10¹ + 3×10⁰ = 100 + 20 + 3 = 123

3、二进制系统

二进制是计算机使用的基本计数系统：

• 采用"满二进一"的规则

• 每一位都是0或1

• 每一位都有对应的位权（2的幂次方）

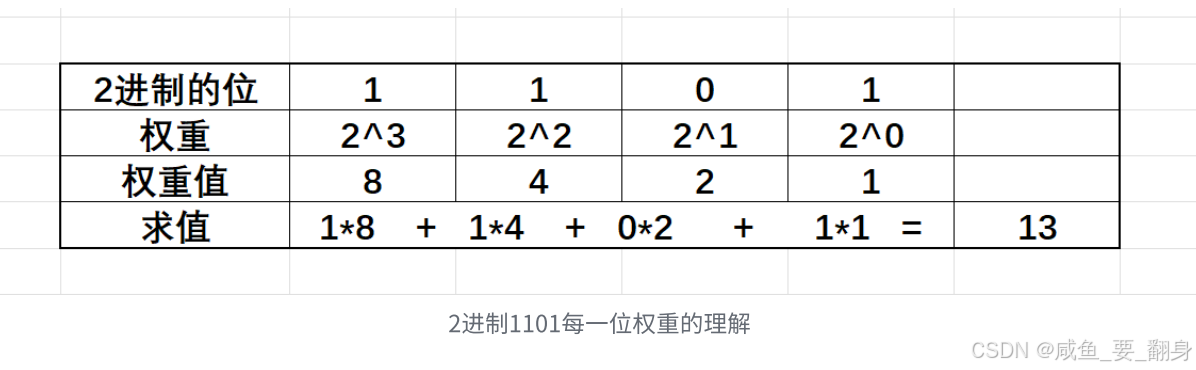
例如，二进制数1101表示：1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 8 + 4 + 0 + 1 = 13（十进制）

---

二、进制转换方法

1、二进制转十进制

        十进制数123表示的数值是一百二十三。这个数值的计算原理在于十进制中每一位数字都带有特定的位权：从右至左分别是个位、十位、百位...，对应的位权依次是10⁰、10¹、10²...如图所示：

        二进制和十进制原理相似，区别在于二进制每一位的权重从右到左依次是2⁰、2¹、2²...以二进制数1101为例，可以这样理解：

2、十进制转二进制

常用"除2取余法"：

1. 将十进制数除以2，记录余数

2. 将商继续除以2，直到商为0

3. 将余数倒序排列即为二进制表示

3、二进制与八进制/十六进制转换

由于8=2³，16=2⁴，因此可以按位分组转换：

二进制转八进制：

• 从右向左每3位一组

• 将每组转换为对应的八进制数字

• 不足3位时左侧补0

例如：01101011 → 001 101 011 → 1 5 3 → 0153（0开头的数字，会被当做8进制）

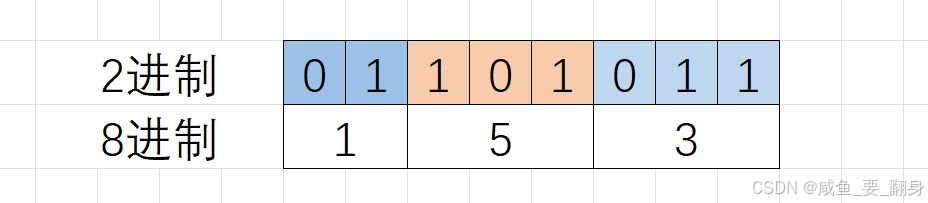
二进制转十六进制：

• 从右向左每4位一组

• 将每组转换为对应的十六进制数字

• 不足4位时左侧补0

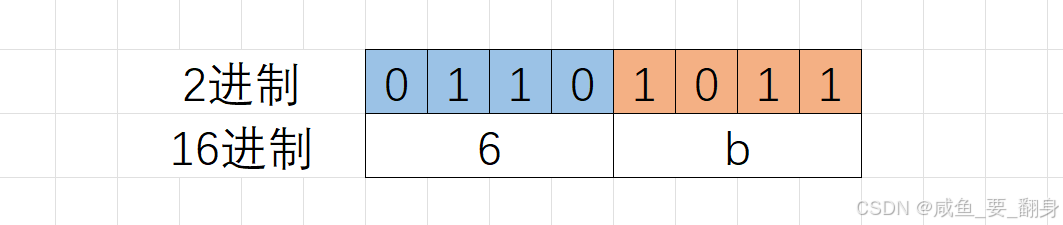
例如：01101011 → 0110 1011 → 6 B → 0x6B（16进制表示的时候前面加0x）

---

三、负数的表示：原码、反码和补码

1、基本概念

整数的二进制表示方法包括三种形式：原码、反码和补码。

        对于有符号整数，这三种表示方法都包含符号位和数值位两部分。在二进制序列中，最高位作为符号位（0表示正数，1表示负数），其余位则为数值位。

正整数的原码、反码和补码表示完全相同。而负整数的三种表示方法则各不相同：

1. 原码：直接将数值的正负形式转换为二进制
2. 反码：保持符号位不变，其他位按位取反
3. 补码：在反码基础上加1

需要注意的是，从补码转换回原码同样可以通过"取反后加1"的操作实现。

2、示例

以8位二进制表示数字5和-5：

• 5：原码：00000101、反码：00000101、补码：00000101

• -5：原码：10000101、反码：11111010、补码：11111011

3、补码的重要性

计算机内部使用补码存储数值，原因在于：

1. 统一了正负数的表示方式

2. 简化了加减法运算（减法可以转换为加法）

3. 解决了原码中"正负零"的问题

4. 硬件实现更简单（不需要额外的减法电路）

例如，计算5 + (-5)：

  00000101 (5的补码)
+ 11111011 (-5的补码)
= 00000000 (结果为0)

---

四、总结

理解二进制和进制转换是计算机科学的基础。掌握这些概念有助于：

• 理解计算机如何存储和处理数据

• 进行底层编程和调试

• 优化算法和数据结构

• 理解计算机网络和加密技术等高级概念

        通过练习各种进制间的转换，可以加深对这些概念的理解，为后续学习计算机组成原理、操作系统等课程打下坚实基础。