当前位置：首页 > news >正文

opencv：傅里叶变换有什么用？怎么写傅里叶变换？

news 2025/8/15 10:23:33

时域与频域，傅里叶变换是干什么的？

什么是时域？什么是频域？这里不做赘述，下面这篇文章讲的很清楚明了，膜拜一下大佬：

https://zhuanlan.zhihu.com/p/19763358

opencv中的傅里叶变换

傅里叶变换的作用

高频：变化剧烈的灰度分量，例如边界
低频：变化缓慢的灰度分量，例如一片大海

滤波

低通滤波器：只保留低频，会使得图像变模糊
高通滤波器：只保留高频，绘制的图像细节增强

代码怎么写？

opencv中主要就是cv2.dft()和cv2.idft(),输入图像需要先转换成np.float32 格式。
得到的结果中频率为0的部分会在左上角,通常要转换到中心位置,可以通过shift变换来实现。
cv2.dft()返回的结果是双通道的(实部,虚部),通常还需要转换成图像格式才能展示(0,255)。

# 获取灰度图
img = cv2.imread("img1.jpg", cv2.IMREAD_GRAYSCALE)
# 输入图像转换成 np.float32 格式
img_float32 = np.float32(img)
# 执行傅里叶变换
dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)# 将低频的值转换到图像中间
# 默认情况下，傅里叶变换的结果中低频分量位于图像的四个角。
# 为了将低频分量移到图像中心，我们使用`fftshift`函数。
# 这个操作将四角中的低频区域移动到图像中心，这样更符合我们的观察习惯（中心是低频，向外是高频）。
dft_shift = np.fft.fftshift(dft)# 得到灰度图能表示的形式
# 这一步是将傅里叶变换的复数结果转换为幅度谱（即频率成分的强度），并将其转换为对数尺度以便于显示。
# “cv2.magnitude”计算复数的幅度（模）。输入两个参数：实部（`dft_shift[:, :, 0]`）和虚部（`dft_shift[:, :, 1]`）。
# 它计算每个点的幅度：`sqrt(real^2 + imag^2)`。
# 由于幅度值可能非常大（而且通常集中在低频部分），我们使用对数变换“np.log”来压缩动态范围。
# 最后，乘以20是为了增强对比度（对数变换后，数值范围被压缩，乘以一个系数可以放大差异，使图像更清晰）。
# 简单来说 20 * np.log 可以将结果转换到0-255这个区间，方便显示
# 这样得到的`magnitude_spectrum`是一个二维数组，表示频率域的幅度谱，通常用于显示。
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))# 显示
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

低通滤波

既然我们已经知道，低频在中心，高频在四角，那进行一次掩码操作不就可以完成低通滤波了吗？（如下图所示）

img = cv2.imread("img1.jpg", cv2.IMREAD_GRAYSCALE)img_float32 = np.float32(img)dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)  # 低频放中心rows, cols = img.shape  # 图像长宽
crow, ccol = int(rows / 2), int(cols / 2)  # 图像中心# 低通滤波
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1    # 掩码图像中心为1# IDFT(傅里叶逆变换，即 傅里叶->原图)
fshift = dft_shift * mask  # 掩码像素为1的保留，为0的归零
f_ishift = np.fft.ifftshift(fshift)  # 低频放回四角，回原来位置
img_back = cv2.idft(f_ishift)  # 傅里叶逆变换，但得到的仍含有实部和虚部，需要处理
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])  # 处理实部和虚部plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('Result'), plt.xticks([]), plt.yticks([])
plt.show()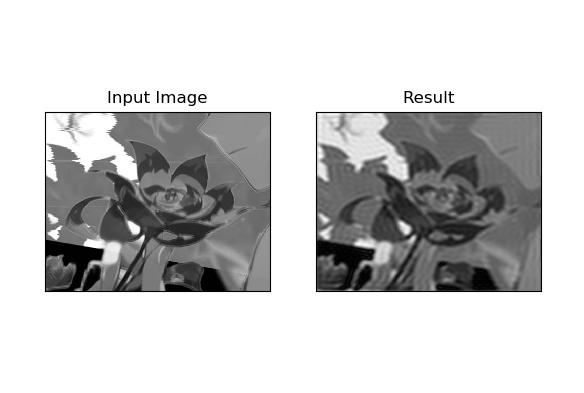

很明显可以看出，低通滤波使图像变模糊了。

高通滤波

高通滤波器和低通滤波器的思路是一样的，同样是创建一个掩码图像，如下图所示：

代码相对于低通滤波修改的很少，只有“高通滤波”部分不一样。

img = cv2.imread("img1.jpg", cv2.IMREAD_GRAYSCALE)img_float32 = np.float32(img)dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)  # 低频放中心rows, cols = img.shape  # 图像长宽
crow, ccol = int(rows / 2), int(cols / 2)  # 图像中心# 高通滤波
mask = np.ones((rows, cols, 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0  # 掩码图像中心为0# IDFT(傅里叶逆变换，即 傅里叶->原图)
fshift = dft_shift * mask  # 掩码像素为1的保留，为0的归零
f_ishift = np.fft.ifftshift(fshift)  # 低频放回四角，回原来位置
img_back = cv2.idft(f_ishift)  # 傅里叶逆变换，但得到的仍含有实部和虚部，需要处理
img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])  # 处理实部和虚部plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('Result'), plt.xticks([]), plt.yticks([])
plt.show()