TensorFlow深度学习实战（32）——深度Q网络（Deep Q-Network，DQN）

0. 前言

深度Q网络 (Deep Q-Network, DQN) 是一种结合了深度学习和强化学习的算法，旨在解决传统Q学习在处理大规模、复杂状态空间时遇到的问题，通过使用深度神经网络来近似Q值函数，使得算法能够在具有高维输入(如图像)的问题上进行有效训练。本节中，介绍了 DQN 的原理、实现与应用，通过理论与实践相结合的方式，详细介绍了如何使用 TensorFlow 构建和训练 DQN。

1. 深度Q网络原理

深度Q网络 (Deep Q-Network, DQN) 是一种用于逼近Q函数(值-状态函数)的深度学习神经网络，是最受欢迎的基于值的强化学习算法之一。该模型由谷歌的 DeepMind 提出，最重要的贡献在于直接将原始状态空间作为网络输入，而不是像早期的强化学习实现那样手工设计输入特征。此外，能够用完全相同的架构训练智能体进行不同的 Atari 游戏，并获得优异结果。
该模型是简单Q学习算法的扩展。在Q学习算法中，会维护一个Q表作为查找表。每次执行动作后，Q表会使用贝尔曼 (Bellman) 方程更新：
$$[Q(S_t,A_t)=(1-\alpha )Q(S_t,A_t)+\alpha (R_{t+1}+\gamma \underset{A}{\max }Q(S_{t+1},A_t))$$
其中，$\alpha$ 是学习率，其值在 [0,1] 范围内。第一项表示先前Q值成分，第二项是目标Q值。如果状态和动作数量较小，Q学习效果很好，但对于大规模的状态空间和动作空间，Q学习的扩展性很差。更好的选择是使用深度神经网络作为函数逼近器，为每个可能的动作近似目标Q函数。在这种情况下，深度神经网络的权重存储了Q表的信息。对于每个可能的动作，网络都有一个单独的输出单元。网络将环境状态作为输入，并返回所有可能动作的预测目标Q值。
网络预测目标Q值：
$$Q_{target}=R_{t+1}+\gamma \underset{A}{\max }Q(S_{t+1},A_t)$$
损失函数的目标是减少预测Q值 $Q_{predicted}$ 和目标Q值 $Q_{target}$ 之间的差异：
$$loss=E_{\pi }[Q_{target}(S,A)-Q_{predicted}(S,W,A)]$$
其中，$W$ 是深度Q网络的可训练参数，通过梯度下降学习，以最小化损失函数。
DQN 的经典架构如下所示，网络以 $n$ 维环境状态作为输入，并输出 $m$ 维动作空间中每个可能动作的Q值。每个网络层(包括输入层)可以是卷积层(如果以原始像素作为输入，卷积层更为合适)或全连接层：

接下来，使用 Tensorflow 训练 DQN 模型，智能体的任务是使杆在小车上保持稳定，智能体可以左右移动小车以维持平衡。

2. 构建 DQN 解决 CartPole问题

CartPole 是一个经典问题，具有连续的状态空间和离散的动作空间。在这个问题中，一根杆通过一个节点连接到一个小车上，小车在无摩擦的轨道上移动。目标是通过左右移动小车保持杆在小车上直立。每次杆保持竖立时都会获得 +1 的奖励，如果杆偏离垂直角度超过 15 度，或者小车距离中心超过 2.4 个单位，游戏结束。

(1) 首先导入所需的模块。使用 gymnasium 提供 CartPole 环境，使用 tensorflow 构建 DQN 网络，此外，还需要 random 和 numpy 模块：

import random
import gymnasium as gym
#import math
import numpy as np
from collections import deque
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam

(2) 设置常量，包括训练智能体的最大回合数 EPOCHS、环境成功解决的阈值 THRESHOLD，指示是否记录训练过程的布尔值 MONITOR。当智能体能够将杆维持在垂直位置 195 个时间步时，可以认为 CartPole 环境已解决。在本节中，为了节省训练时间，将 THRESHOLD 减少到了 45：

EPOCHS = 1000
THRESHOLD = 45
MONITOR = True

(3) 构建 DQN 模型。声明一个 DQN 类，在其 __init__() 函数中声明超参数和模型，并在 DQN 类中创建环境：

class DQN():def __init__(self, env_string,batch_size=64):self.memory = deque(maxlen=100000)self.env = gym.make(env_string, render_mode='rgb_array')input_size = self.env.observation_space.shape[0]action_size = self.env.action_space.nself.batch_size = batch_sizeself.gamma = 1.0self.epsilon = 1.0self.epsilon_min = 0.01self.epsilon_decay = 0.995alpha=0.01alpha_decay=0.01lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(initial_learning_rate=alpha,decay_steps=10, decay_rate=1.0 - alpha_decay, staircase=True)if MONITOR: self.env = gym.wrappers.RecordVideo(self.env, 'data/'+env_string, episode_trigger=lambda x: True)# Init modelself.model = Sequential()self.model.add(Dense(24, input_dim=input_size, activation='tanh'))self.model.add(Dense(48, activation='tanh'))self.model.add(Dense(action_size, activation='linear'))self.model.compile(loss='mse', optimizer=Adam(lr_schedule))

通过观察模型摘要，可以看到，本节构建的 DQN 是一个三层全连接网络，优化器使用带有学习率衰减的 Adam 优化器。

变量 self.memory 表示经验回放缓冲池，添加 remember() 方法，用于将 <S,A,R,S’> 元组保存到内存中，添加 replay() 方法，从经验回放缓冲池以批数据形式获取随机样本来训练智能体：

    def remember(self, state, action, reward, next_state, done):self.memory.append((state, action, reward, next_state, done))def replay(self, batch_size):x_batch, y_batch = [], []minibatch = random.sample(self.memory, min(len(self.memory), batch_size))for state, action, reward, next_state, done in minibatch:y_target = self.model.predict(state)y_target[0][action] = reward if done else reward + self.gamma * np.max(self.model.predict(next_state)[0])x_batch.append(state[0])y_batch.append(y_target[0])self.model.fit(np.array(x_batch), np.array(y_batch), batch_size=len(x_batch), verbose=0)#epsilon = max(epsilon_min, epsilon_decay*epsilon) # decrease epsilon

智能体在选择动作时使用ε-贪婪策略：

    def choose_action(self, state, epsilon):if np.random.random() <= epsilon:return self.env.action_space.sample()else:return np.argmax(self.model.predict(state))

接下来，定义 train() 方法训练智能体。定义两个列表跟踪分数，填充经验回放缓冲池，从中选择随机样本训练智能体：

    def train(self):scores = deque(maxlen=100)avg_scores = []for e in range(EPOCHS):state = self.env.reset()state = self.preprocess_state(state[0])done = Falsei = 0while not done:action = self.choose_action(state,self.epsilon)next_state, reward, done, truncated, info = self.env.step(action)next_state = self.preprocess_state(next_state)self.remember(state, action, reward, next_state, done)state = next_stateself.epsilon = max(self.epsilon_min, self.epsilon_decay*self.epsilon) # decrease epsiloni += 1scores.append(i)mean_score = np.mean(scores)avg_scores.append(mean_score)if mean_score >= THRESHOLD and e >= 100:print('Ran {} episodes. Solved after {} trials ✔'.format(e, e - 100))return avg_scoresif e % 100 == 0:print('[Episode {}] - Mean survival time over last 100 episodes was {} ticks.'.format(e, mean_score))self.replay(self.batch_size)print('Did not solve after {} episodes 😞'.format(e))return avg_scores

定义辅助函数重新调整 CartPole 环境状态的形状，以便模型的输入具有正确的形状。环境的状态由四个连续变量描述：小车位置 ([-2.4, 2.4])、小车速度、杆角度 ([-41.8°, 41.8°]) 和杆速度：

    def preprocess_state(self, state):return np.reshape(state, [1, 4])

(4) 实例化 CartPole 环境，并训练智能体：

env_string = 'CartPole-v0'
agent = DQN(env_string)
scores = agent.train()
# [Episode 0] - Mean survival time over last 100 episodes was 28.0 ticks.
# ...
# Ran 104 episodes. Solved after 4 trials ✔

(5) 绘制智能体学习过程中的平均奖励：

import matplotlib.pyplot as plt
plt.plot(scores)
plt.show()print(agent.model.summary())

智能体在 CartPole 环境中的训练过程如下，可以看到，智能体能够快速达到设定的阈值 (45)：

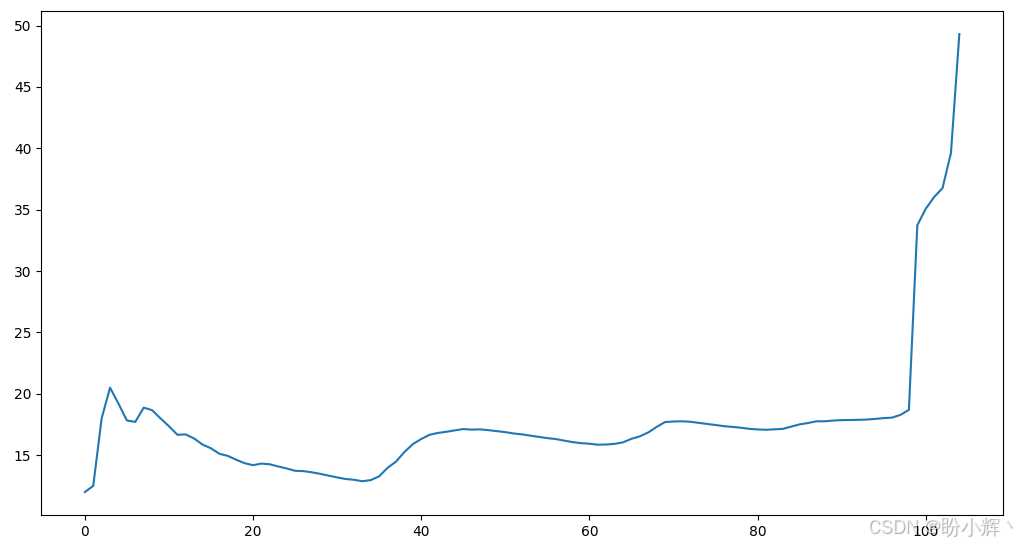
(6) 训练完成后，关闭环境：

agent.env.close()

可以看到，一开始没有任何关于如何平衡杆的信息，智能体使用 DQN 能够在学习过程中逐渐平衡杆，平均时间越来越长，智能体能够从零开始积累信息/知识实现预期目标。

3. DQN 变体

在 DQN 取得成功之后，引发了对强化学习的热潮，许多新的强化学习算法随之出现。接下来，我们将介绍一些基于 DQN 的变体算法。

3.1 Double DQN

在 DQN 中，智能体使用相同的Q值来选择和评估一个动作。这可能会导致学习中的最大化偏差。例如，假设对于某个状态S，所有可能的动作的真实Q值都为零。此时，DQN 估计值将会有一些高于零的值和一些低于零的值，由于选择具有最大Q值的动作，并且后续使用相同(最大化的)估计值函数评估每个动作的Q值，智能体就会高估Q值，换句话说，智能体过于乐观，这可能导致训练不稳定和低质量的策略。为了解决这个问题，DeepMind 提出了 Double DQN 算法。在 Double DQN 中，有两个具有相同结构但权重不同的Q网络。其中一个Q网络使用ε-贪婪策略确定动作，另一个Q网络确定其值 ($Q_{target}$)。
在 DQN 中，$Q_{target}$ 目标计算方式如下：
$$Q_{target}=R_{t+1}+\gamma \underset{A}{\max }Q(S_{t+1},A_t)$$
其中，动作 $A$ 是使用相同的 DQN $Q(S,A;W)$ 选择的，其中 $W$ 是网络的训练参数：
$$Q_{target}=R_{t+1}+\gamma \underset{A}{\max }Q(S_{t+1},argma{x}_{t}Q(S,A;W);W)$$
在 Double DQN 中，目标方程有所不同，DQN $Q(S,A;W)$ 用于确定动作，而 DQN $Q(S,A;W^{\prime })$ 用于计算目标。因此，方程将改写为：
$$Q_{target}=R_{t+1}+\gamma \underset{A}{\max }Q(S_{t+1},argma{x}_{t}Q(S,A;W);W^{\prime })$$
这一简单的更改减少高估Q值的可能性，并且能够更快、更可靠地训练智能体。

3.2 Dueling DQN

Dueling DQN 由 Wang 等人提出，与 DQN 和 Double DQN 一样，它也是一种无模型算法。Dueling DQN 将Q函数分解为值函数和优势函数。值函数表示状态的值，与动作无关。另一方面，优势函数提供了在状态 $S$ 中动作 $A$ 的相对优势性的度量。Dueling DQN 在初始层使用卷积网络从原始像素中提取特征，但在后续阶段，网络分为两个不同的分支，一个用于近似值，另一个用于近似优势性度量。确保了网络为值函数和优势函数生成单独的估计：
$$Q(S,A)=A(S,A;\theta ,\alpha )+V^{\pi }(S;\theta ,\beta )$$
其中，$\theta$ 是共享卷积网络的训练参数数组(由 $V$ 和 $A$ 共享)，而 $\alpha$ 和 $\beta$ 是优势和值估计网络的训练参数。随后，这两个网络通过聚合层重新组合，以估计Q值。
Dueling DQN 的架构如下所示。

分解值函数和优势函数可以了解哪些状态是有价值的，而不必考虑每个状态下每个动作的影响。因此，分离值和优势可以更稳定地近似值函数。在下图中可以看到，在 Atari 游戏，值网络学习关注道路，而优势网络学习仅在前方有汽车时才会关注，以避免碰撞：

在聚合层的实现中，强制优势函数估计器在选择的动作下的优势为零，使得可以从给定的Q值中恢复出值 $V$ 和优势 $A$：
$$Q(S,A;\theta ,\alpha ,\beta )=A(S,A;\theta ,\alpha )+V^{\pi }(S;\theta ,\beta )-ma{x}_{a^{\prime }\in |A|}A(S,A^{\prime };\theta ,\alpha )$$
如果将最大操作替换为平均操作，网络会更稳定，因为在这种情况下，优势的变化速度与平均的变化速度相同，而不是与最佳(最大)值的变化速度相同。

3.3 Rainbow

严格来说，将 Rainbow 称为 DQN 变体并不准确。实际上，Rainbow 是将多个 DQN 变体组合成一个单一算法的集合体，它将分布式强化学习 (distributional RL) 损失修改为多步损失，并将其与使用贪婪动作的 Double DQN 相结合。
Rainbow 网络具有一个共享表示 $f_{\xi }(s)$，然后输入到一个具有 $N_{atoms}$ 输出的值流 $v_{\eta }$ 和一个具有 $N_{atoms}\times N_{actions}$ 输出的优势流 $a_{\xi }$ 中，其中 $a_{i\xi }(f_{\xi }(s),a)$ 表示与原子 $i$ 和动作 $a$ 对应的输出。在 Rainbow 中，原子指的是在分布式强化学习中用于表示状态-动作值分布的基本单位。具体来说，原子是在智能体学习到的回报分布中每个可能的值的一个离散表示。对于每个原子 $z_i$，值流和优势流进行聚合，与 Dueling DQN 相同，然后通过 softmax 层得到用于估计回报分布的标准化参数分布。
Rainbow 结合了六种不同的强化学习算法：

• N 步返回
• 分布式状态-动作值学习
• 对抗网络 (Dueling DQN)
• 噪声网络
• Double DQN
• 优先经验回放

小结

深度Q网络 (Deep Q-Network, DQN) 通过结合深度学习和强化学习，成功地解决了高维状态空间中的决策问题，核心创新在于使用深度神经网络来近似Q函数，同时引入经验回放和目标网络来提高训练的稳定性和效率。DQN 的成功为深度强化学习的发展奠定了基础，并推动了多种先进算法的研究和应用。

系列链接

TensorFlow深度学习实战（1）——神经网络与模型训练过程详解
TensorFlow深度学习实战（2）——使用TensorFlow构建神经网络
TensorFlow深度学习实战（3）——深度学习中常用激活函数详解
TensorFlow深度学习实战（4）——正则化技术详解
TensorFlow深度学习实战（5）——神经网络性能优化技术详解
TensorFlow深度学习实战（6）——回归分析详解
TensorFlow深度学习实战（7）——分类任务详解
TensorFlow深度学习实战（8）——卷积神经网络
TensorFlow深度学习实战（9）——构建VGG模型实现图像分类
TensorFlow深度学习实战（10）——迁移学习详解
TensorFlow深度学习实战（11）——风格迁移详解
TensorFlow深度学习实战（12）——词嵌入技术详解
TensorFlow深度学习实战（13）——神经嵌入详解
TensorFlow深度学习实战（14）——循环神经网络详解
TensorFlow深度学习实战（15）——编码器-解码器架构
TensorFlow深度学习实战（16）——注意力机制详解
TensorFlow深度学习实战（17）——主成分分析详解
TensorFlow深度学习实战（18）——K-means 聚类详解
TensorFlow深度学习实战（19）——受限玻尔兹曼机
TensorFlow深度学习实战（20）——自组织映射详解
TensorFlow深度学习实战（21）——Transformer架构详解与实现
TensorFlow深度学习实战（22）——从零开始实现Transformer机器翻译
TensorFlow深度学习实战（23）——自编码器详解与实现
TensorFlow深度学习实战（24）——卷积自编码器详解与实现
TensorFlow深度学习实战（25）——变分自编码器详解与实现
TensorFlow深度学习实战（26）——生成对抗网络详解与实现
TensorFlow深度学习实战（27）——CycleGAN详解与实现
TensorFlow深度学习实战（28）——扩散模型（Diffusion Model）
TensorFlow深度学习实战（29）——自监督学习（Self-Supervised Learning）
TensorFlow深度学习实战（30）——强化学习（Reinforcement learning，RL）
TensorFlow深度学习实战（31）——强化学习仿真库Gymnasium