算法提升-树上问题之（dfs序）

今天带来分享的是关于树中dfs序的相关内容，简而言之，通过dfs序可以将树上的问题转化为数组的问题，即通过dfn数组将进行标号。同时通过idx数组将节点的信息存入dfn中。用来处理某些子树问题很方便

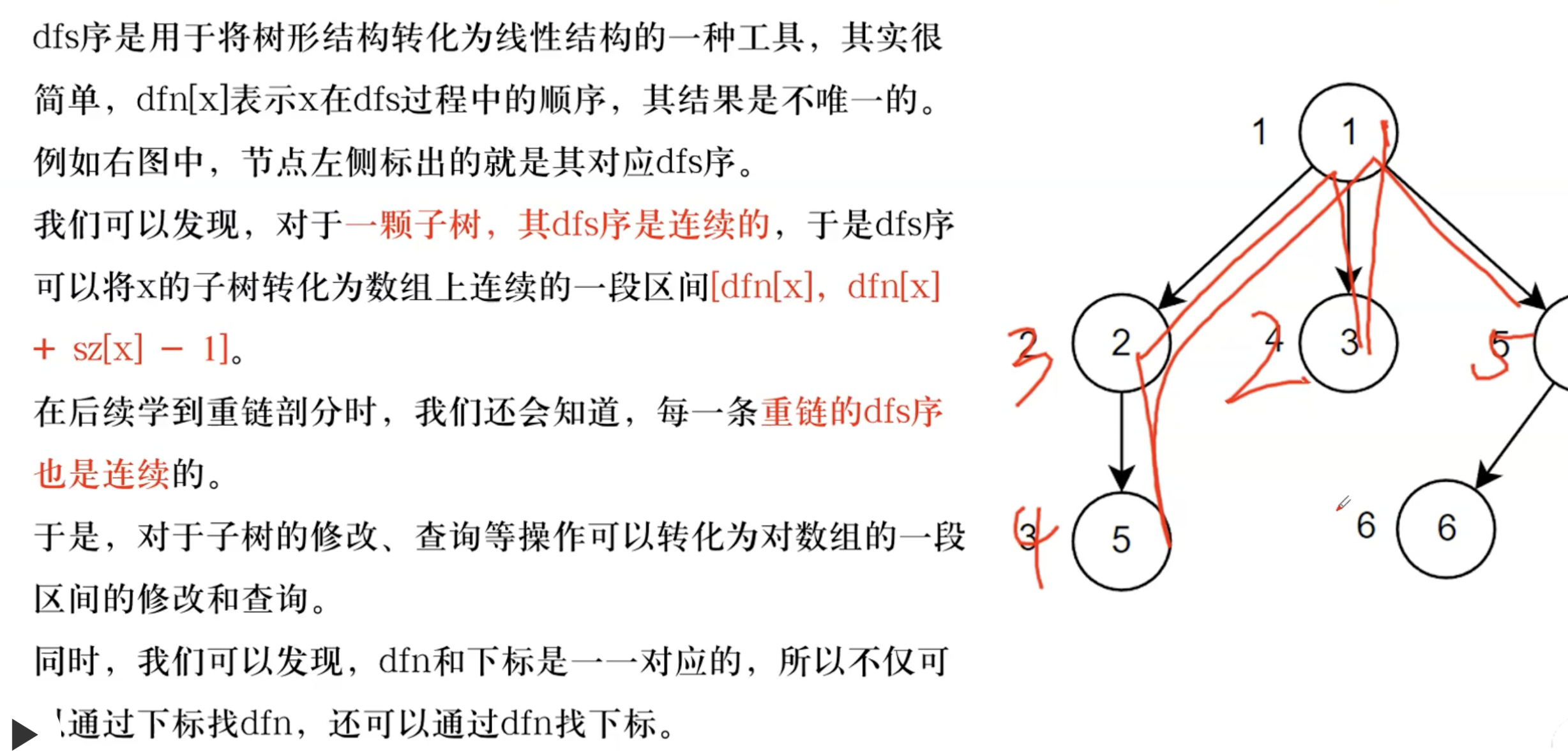
核心代码部分

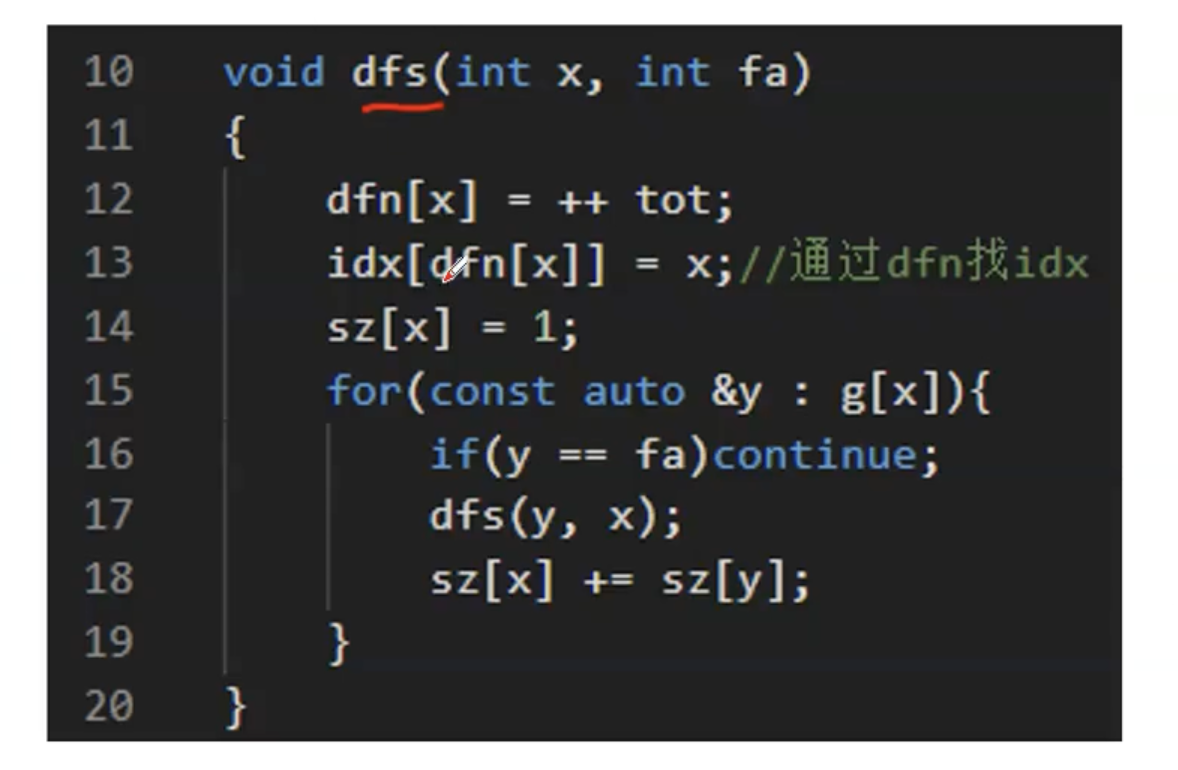
接下来通过几道例题来帮助大家更好地理解有关dfs序的相关信息。

问题描述

一天，小蓝在他的小屋外发现了一颗神奇的树，它的树叶上闪烁着各种不同的颜色。小蓝对这颗树产生了浓厚的兴趣，于是他决定研究这颗树的奥秘。这棵树被称为"奇幻之树"，因为它拥有神奇的能力。

每个节点都有自己独特的颜色，这些颜色代表了树上不同生物的种类。小蓝注意到，树的每个节点都有一个颜色标签 ci​ ，而这些颜色标签在树上不断变化，使得树上的生物多样性持续增加。

小蓝决定用算法来研究这颗树。他提出了一些问题，希望能够了解奇幻之树上不同颜色的种类数量。每次他会选择一颗树上的节点，然后探索以这个节点为根的子树中的颜色种类。

具体问题如下：给定一棵节点为 n 的有根树，根节点为 1 ，每个节点有一个颜色 ci，小蓝有 q 组询问，每次询问给定一个节点 x ，问 x 为根的子树中，有多少种不同的颜色。

小蓝很期待你能够帮助他解决这些有趣的问题，揭示奇幻之树的神奇之处。每次你回答一个询问，都会让小蓝对这颗树的理解更进一步，同时也会使他的奇幻之旅变得更加精彩。

输入格式

第一行输入两个整数 n,q。代表树的节点数量与询问数量。

接下来一行，输入 n 个整数 c1​,c2​,c3​...cn​ ， 代表每个节点的颜色。

接下来 n−1 行，每行两个整数 ui​,vi​ ，代表存在一条边连接 ui​,vi​ 两点。

接下来 q 行， 每行一个整数 xi​ ，代表询问的点。

输出格式

输出 q 行，每行一个整数，代表每次询问的答案。

输入案例：

5 3
1 2 3 4 5
1 2
1 3
2 4
2 5
1
2
3

输出案例：

5
3
1

#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 1e5+5;
int n,c[N];
vector<int> g[N];
int sz[N],dfn[N],idx[N],tot;
int pre[N][101];void dfs(int x,int fa){sz[x]=1;dfn[x]=++tot;idx[dfn[x]]=x;for(const auto &y:g[x]){if(y==fa) continue;dfs(y,x);sz[x]+=sz[y];}
}void solve() {int x;cin>>x;int l=dfn[x],r=l+sz[x]-1;int ans=0;for(int i=1;i<=100;i++){if(pre[r][i]-pre[l-1][i]>0) ans++;}cout<<ans<<endl;
}
int main() {ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;int q;cin>>q;for(int i=1;i<=n;i++) cin>>c[i];for(int i=2;i<=n;i++){int x,y;cin>>x>>y;g[x].push_back(y);g[y].push_back(x);}dfs(1,0);for(int i=1;i<=100;i++){for(int j=1;j<=n;j++){pre[j][i]=pre[j-1][i]+(c[idx[j]]==i);}}while(q--) {solve();}return 0;
}

这道题是经典的有关dfs序的问题，通过dfs序转化来对树中的有关问题进行求解分析，希望大家可以好好理解这道题目。

问题描述

给一棵含有 n 个结点的有根树，根结点为 1，编号为 i的点有点权 ai（i∈[1,n]）。现在有两种操作，格式如下：

• 1 x y：该操作表示将点 x 的点权改为 y。
• 2 x：该操作表示查询以结点 x 为根的子树内的所有点的点权的异或和。

现有长度为 m的操作序列，请对于每个第二类操作给出正确的结果。

输入格式

输入的第一行包含两个正整数 n,m，用一个空格分隔。

第二行包含 n 个整数 a1​,a2​,…,an​，相邻整数之间使用一个空格分隔。

接下来 n−1行，每行包含两个正整数 ui​,vi​，表示结点 ui​ 和 vi​ 之间有一条边。接下来 m 行，每行包含一个操作。

输出格式

输出若干行，每行对应一个查询操作的答案。

输入案例：

4 4
1 2 3 4
1 2
1 3
2 4
2 1
1 1 0
2 1
2 2

输出案例：

4
5
6

代码部分：

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int wei[N],wi[N];
vector<int>a[N];
int cnt=0;
int in[N],out[N];
void dfs(int x,int fa){in[x]=++cnt;wi[in[x]]=wei[x];for(const auto&t:a[x]){if(t==fa)continue;dfs(t,x);}out[x]=cnt;
}
int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++)cin>>wei[i];for(int i=1;i<n;i++){int u,v;cin>>u>>v;a[u].push_back(v),a[v].push_back(u);}dfs(1,0);while(m--){int c;cin>>c;if(c==1){int x,y;cin>>x>>y;wi[in[x]]=y;}else{int d;cin>>d;int ans=0;for(int i=in[d];i<=out[d];i++){ans=ans^wi[i];}cout<<ans<<'\n';}}return 0;
}

这两道题都是通过dfs序来进行解决的，好了今天的分享就到这里，大家多多关注，后续也将继续进行相关内容分享。