论区间dp:常用模型（附极角排序教程）

前言

区间dp很简单，重要的是判断在什么样的题里用区间$dp$
本文适合对区间$dp$有初步了解的人阅读
本文有三道例题
1.P1220 关路灯
2.青蛙的烦恼
3.行政划分

例1.关路灯

题面如下

一看题面，似乎找不到什么规律，难道要状压？肯定不行，会TLE
仔细想想，关掉的路灯必然是连续的，如下图

红色的路线一定优于蓝色路线，蓝色在由$3$走到$5$时，沿途关掉$4$将会取得更优解，途中红色就是这种做法
也就是说，不允许有“回首掏”操作的出现
这个很重要，基本的区间dp有明显的区间，而更普遍的情况就如这题，区间其实是隐藏起来的，不允许回首掏，那么必然连续，则可以形成区间，使用区间dp
接下来的步骤就简单多了，设状态$dp[i][j][k]$为关掉区间$[i,j]$的所有路灯的最小花费，如最后关掉的路灯位于区间左端点，$k$为$0$，位于右端点则为$1$
$dp[i][j][0]$可由$dp[i+1][j][0]$和$dp[i+1][j][0]$转移得到，$dp[i][j][1]$同理
状态转移方程如下
$dp[i][j][0]=min(dp[i+1][j][0]+dist\ast w,dp[i+1][j][1]+dist\ast w)$
$dp[i][j][1]=min(dp[i][j-1][1]+dist\ast w,dp[i][j-1][0]+dist\ast w)$
注意，$dist$为所要走的路径长，互相之间不相等，详见代码
$w$为剩余亮着的路灯每秒耗电量，用前缀和可以$O(1)$求
代码在此

#include<bits/stdc++.h>
using namespace std;
int n,c;
int a[100010],p[100010];
int dp[300][300][3];
int sump[100010];
int sp = 0;
int dist[300][300];
int main(){cin>>n>>c;for(int i = 1;i<=250;i++){for(int j = 1;j<=250;j++){dp[i][j][0] = dp[i][j][1] = 2000000000;}}dp[c][c][1] = dp[c][c][0] = 0;for(int i = 1;i<=n;i++){cin>>a[i]>>p[i];sp+=p[i];sump[i] = sump[i-1]+p[i];}for(int i = 1;i<=n;i++){for(int j = i;j<=n;j++){dist[i][j] = a[j]-a[i];}}for(int len = 2;len<=n;len++){for(int i = 1,j = i+len-1;j<=n;i++,j++){dp[i][j][0] = min(dp[i+1][j][0]+(a[i+1]-a[i])*(sp-sump[j]+sump[i]),dp[i+1][j][1]+(dist[i][j])*(sp-sump[j]+sump[i]));dp[i][j][1] = min(dp[i][j-1][1]+(a[j]-a[j-1])*(sp-sump[j-1]+sump[i-1]),dp[i][j-1][0]+(dist[i][j])*(sp-sump[j-1]+sump[i-1]));}}cout<<min(dp[1][n][0],dp[1][n][1]);return 0;
}

例2.青蛙的烦恼

依旧先给题面

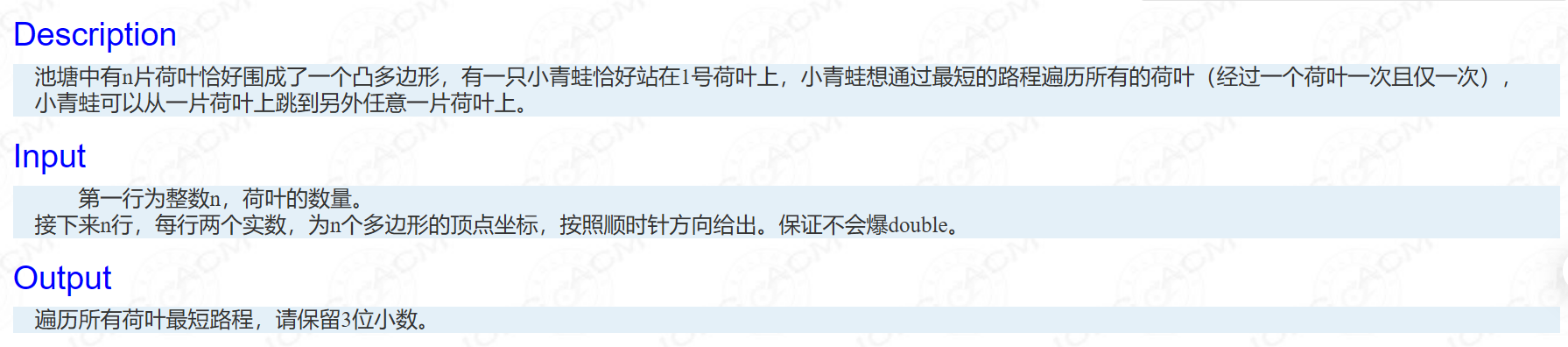
这题更抽象了，像极了最短Hamilton路径(状压dp，请看我的博客)
唯一的区别就在凸多边形，貌似没用，但是我们可以想一想，如果是最简单的四边形，情况是什么样呢？

容易想得到图中红色和蓝色的路径，那么哪个更优呢，必定是红色的
首先，两条路径均经过边$23$，不考虑
然后，根据三角形两边之和大于第三边，得出了$12+34$小于$13+24$(此处数字表示边)
你一定也发现了规律，边不能交叉，这就导致了这题中回首掏操作一定不为最优解
那么又能得出什么呢？青蛙到过的点是连续的！区间有了，区间$dp$启动！
我们先破环为链，再倍长，这是解决环形问题的基本步骤
然后就和上一题没什么区别了
代码如下

#include<bits/stdc++.h>
using namespace std;
int n;
double ans = 100000000.00;
struct node{double x,y;
}a[114514];
double dp[1500][1500][2];
double dist(node a,node b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int main(){cin>>n;for(int i = 1;i<=n;i++){cin>>a[i].x>>a[i].y;a[i+n].x = a[i].x;a[i+n].y = a[i].y;}memset(dp,0x7f,sizeof(dp));dp[1][1][0] = dp[1][1][1] = dp[n+1][n+1][0] = dp[n+1][n+1][1] = 0;for(int len = 2;len<=n;len++){for(int i = 1,j = i+len-1;j<=n+n;i++,j++){dp[i][j][0] = min(dp[i][j][0],dp[i+1][j][0]+dist(a[i],a[i+1]));dp[i][j][0] = min(dp[i][j][0],dp[i+1][j][1]+dist(a[i],a[j]));dp[i][j][1] = min(dp[i][j][1],dp[i][j-1][0]+dist(a[j],a[i]));dp[i][j][1] = min(dp[i][j][1],dp[i][j-1][1]+dist(a[j],a[j-1]));}}for(int i = 1;i<=n;i++){ans = min(ans,dp[i][i+n-1][0]);ans = min(ans,dp[i][i+n-1][1]);}printf("%.3lf",ans);return 0;
}

例3.行政划分

题面

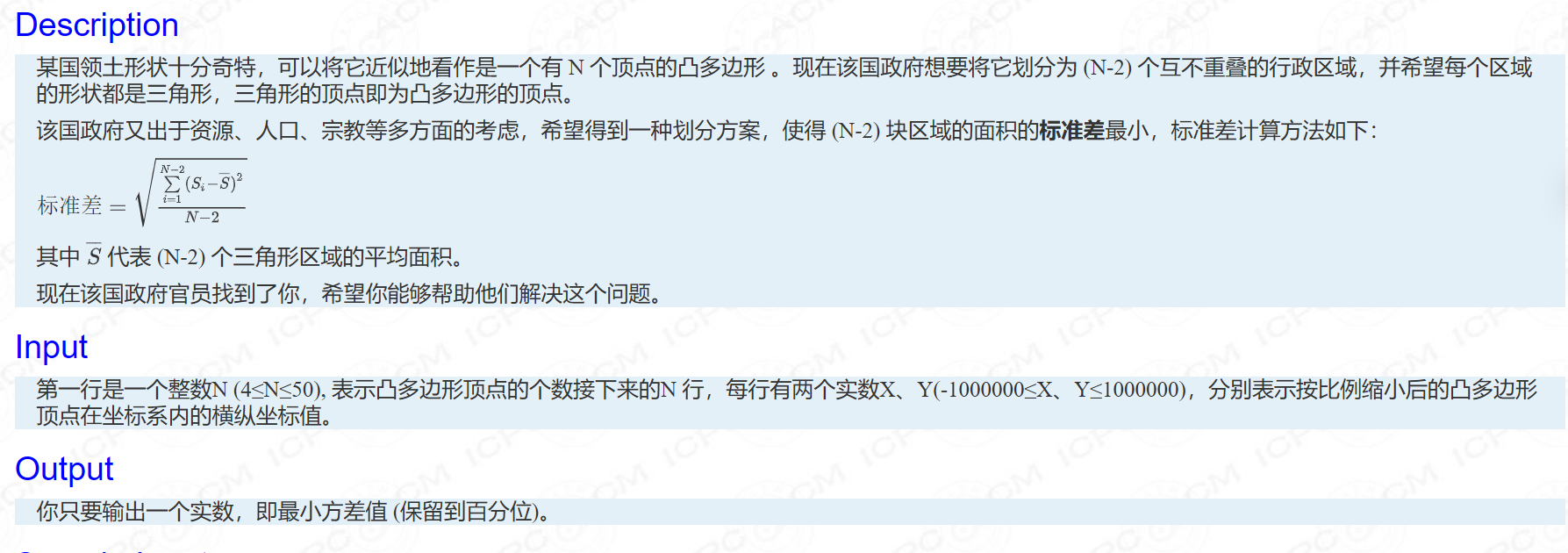
看到这个题，无论是谁都不会先想$dp$的，当务之急是解决那一串式子
我们可以先用完全平方公式，变形过程如下

$S$平均和$S$和$N$都定了，我们求最小$\Sigma S_i^2$就行了
这一题的线性$dp$更加明显，既然是分割，边就不能交叉，这样就不能回首掏，得到区间，区间$dp$再次启动
求三角形面积可以用海伦公式
设置状态$dp[i][j]$为分割完点从$i$到$j$的最小$\Sigma S_i^2$
初始设置每个$dp[i][i+1]$为$0$，状态的转移可以枚举区间断点
如区间$[i,j]$，边界$i,j$和断点$k$可以构成三角形，并上$dp[i][k]$和$dp[k][j]$即可得到整个区间
可以看下图

可以得出状态转移方程
$dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+h\ast h);$
注:$h$为三角形$ijk$的面积
然而到这还没完，题目中给定的点并不是按照一定顺序给的，我们要把它们排成顺时针或逆时针
这就要用到极角排序了
（以下内容和区间$dp$关系不大，如不想解决本题可以跳过）
极角排序就是选定一个原点，利用反正切函数来按照不同点和原点之间的极角大小来排序（反正切函数可以看作一定范围内，正切函数的反函数）
我们将原点选在这个凸包$y$坐标的最低点，如有多个最低点则选择靠左的一个，然后使用c++的$atan2(y,x)$函数，输入$y,x$坐标即可计算角度，与正常的反正切函数不同，本函数算出的角度属于$0$到$180$度，是的，$90$度也能算，简直就是为极角排序专门设计的,orz%%%
代码这样写（极角排序）

bool cmp(node p,node q){if(atan2(p.y-miny,p.x-minx)!=atan2(q.y-miny,q.x-minx))return atan2(p.y-miny,p.x-minx)<atan2(q.y-miny,q.x-minx);else return p.x<q.x;
}
void jijiao_sort(){cin>>n;for(int i = 1;i<=n;i++){cin>>a[i].x>>a[i].y;if(a[i].y<miny||(a[i].y==miny&&a[i].x<minx)){miny = a[i].y;minx = a[i].x;}}sort(a+1,a+n+1,cmp);return;
}

注意了，为了防止原点不排在最前面，$cmp$函数里必须要判断$arctan$的值是否相等，如相等将左侧的点排在前面，必须，必须，必须，否则遇到$y$坐标相等就会排乱，将原点放在第二位，你就WA了，作者因为这个调了一下午，警示后人！！！
有了极角排序，我们终于可以完成这道题了
代码

#include<bits/stdc++.h>
using namespace std;
int n;
double minx = 1145141919.810,miny = 11145141919.810;
double dp[60][60];
double s,sb; 
struct node{double x,y;
}a[114514];
double get_s(node a,node b,node c){double aa = sqrt((c.x-b.x)*(c.x-b.x)+(c.y-b.y)*(c.y-b.y));double bb = sqrt((c.x-a.x)*(c.x-a.x)+(c.y-a.y)*(c.y-a.y));double cc = sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));double p = (aa+bb+cc)/2;return sqrt(p*(p-aa)*(p-bb)*(p-cc));
}
bool cmp(node p,node q){if(atan2(p.y-miny,p.x-minx)!=atan2(q.y-miny,q.x-minx))return atan2(p.y-miny,p.x-minx)<atan2(q.y-miny,q.x-minx);else return p.x<q.x;
}
void jijiao_sort(){cin>>n;for(int i = 1;i<=n;i++){cin>>a[i].x>>a[i].y;if(a[i].y<miny||(a[i].y==miny&&a[i].x<minx)){miny = a[i].y;minx = a[i].x;}}sort(a+1,a+n+1,cmp);return;
}
int main(){jijiao_sort();for(int i = 3;i<=n;i++){s+=get_s(a[1],a[i],a[i-1]);}sb = s/(n-2);memset(dp,0x7f,sizeof(dp));for(int i = 1;i<=n-1;i++){dp[i][i+1] = 0;}for(int len = 3;len<=n;len++){for(int i = 1,j = i+len-1;j<=n;i++,j++){for(int k = i+1;k<j;k++){double h = get_s(a[i],a[j],a[k]);dp[i][j] = min(dp[i][j],dp[i][k]+dp[k][j]+h*h);}}}double ans = (dp[1][n]-s*sb)/(n-2);if(ans<1e-7){ans = 0;}printf("%.2lf\n",sqrt(ans));return 0;
}

总结

经过了三道例题的训练，相信你也对区间$dp$的套路有一定理解了
区间$dp$的典型特征有区间合并（本文没讲这类，比较基础），不能回首掏，平面几何线段不交叉，看到这些，就多考虑考虑区间$dp$吧
本文作者是蒟蒻，如有错误请各位神犇指点
森林古猿出品，必属精品，请认准CSDN森林古猿1！