我的 LeetCode 日记：Day 35 - 解构动态规划，初探 0/1 背包问题

今天，我怀着无比激动的心情，踏入了一个在算法领域如雷贯耳的经典模型——背包问题。我早就听说过它的鼎鼎大名，也知道它是动态规划中非常重要的一类问题。正如 Carl 哥所说，很多人可能对背包问题的模板代码很熟悉，但对其背后的原理理解得并不深入。因此，我今天的目标只有一个：彻底搞懂 0/1 背包的理论基础，理解其二维和一维（空间优化）的实现原理。

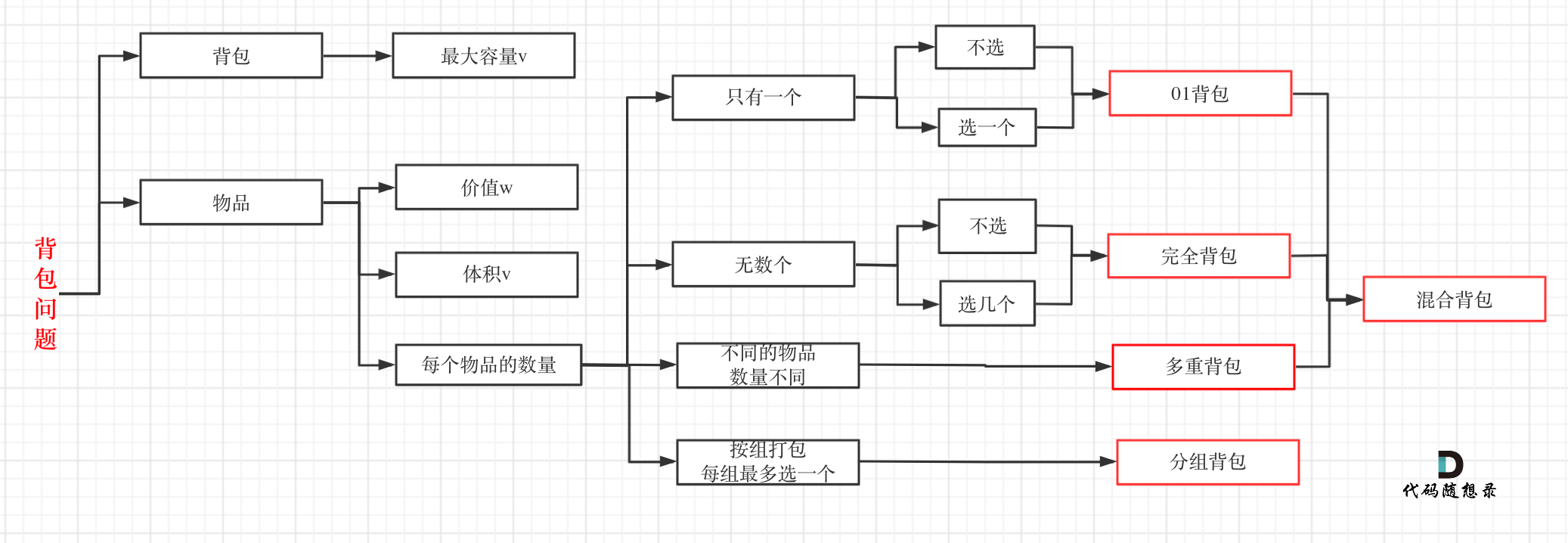
一、理论奠基：0/1 背包问题的核心思想

0/1 背包问题描述的是：有一堆物品，每个物品都有自己的重量和价值，还有一个容量有限的背包。问题是，如何在不超过背包总容量的前提下，选择物品，使得装入背包的物品总价值最大？这里的 “0/1” 指的是，对于每个物品，你要么不选（0），要么选（1），不能只选一部分。

1. 二维 dp 数组解法

这是最直观、最容易理解的解法，完美地体现了 DP 的思想。我依然使用“五部曲”来剖析它：

1. dp 数组定义: dp[i][j] 表示：从下标为 0 到 i 的物品里任意选取，放入容量为 j 的背包，所能获得的最大价值。
2. 状态转移方程: 面对第 i 个物品，我们有两种选择：
   • 不放物品 i：那么 dp[i][j] 的价值就等于只考虑前 i-1 个物品、容量为 j 时的最大价值，即 dp[i-1][j]。
   • 放物品 i（前提是背包容量 j 足够大）：那么价值就是物品 i 的价值，加上背包装下物品 i 后，用剩余容量 j - weight[i] 去装前 i-1 个物品所能获得的最大价值，即 value[i] + dp[i-1][j - weight[i]]。
     最终，dp[i][j] 就是这两者中的较大值：max(不放, 放)。
3. 初始化: dp 数组的第一行和第一列通常可以初始化为 0，表示没有物品或背包没有容量时，最大价值为 0。
4. 遍历顺序: 外层循环遍历物品 i，内层循环遍历背包容量 j。

• 理论指南:
  • 文章讲解: 代码随想录-01背包理论基础(二维)
  • 视频讲解: B站视频-01背包(二维)

我的实现：二维 dp

def knapsack_2d(M, N, weights, values):"""M: 物品数量N: 背包容量weights: 物品重量列表values: 物品价值列表"""# 1. dp[i][j] 定义：从0-i号物品中，放入容量为j的背包的最大价值dp = [[0] * (N + 1) for _ in range(M + 1)]# 4. 遍历顺序：先物品，后背包for i in range(1, M + 1):for j in range(1, N + 1):weight_i = weights[i-1] # 当前物品i的重量value_i = values[i-1]   # 当前物品i的价值# 如果背包容量j装不下物品iif j < weight_i:dp[i][j] = dp[i-1][j] # 不放物品ielse:# 2. 状态转移方程dp[i][j] = max(dp[i-1][j], value_i + dp[i-1][j - weight_i])return dp[M][N]

2. 一维 dp 数组解法（空间优化）

我发现，在计算 dp[i] 这一行时，我们只用到了 dp[i-1] 这一行的信息。因此，可以用一个一维数组来“滚动”更新，将空间复杂度从 O(m*n) 优化到 O(n)。

1. dp 数组定义: dp[j] 表示容量为 j 的背包，所能背的最大价值。
2. 状态转移方程: dp[j] = max(dp[j], dp[j - weight[i]] + values[i])。
3. 初始化: dp 数组全部初始化为 0。
4. 遍历顺序: 这是最关键、最容易出错的地方！外层循环遍历物品 i，内层循环遍历背包容量 j 必须从后往前（倒序）。
   • 为什么必须倒序？ 因为要保证在计算 dp[j] 时，所用到的 dp[j - weight[i]] 是上一轮循环（即 i-1）的结果。如果正序遍历，dp[j - weight[i]] 会被先更新，这样在计算 dp[j] 时，就相当于在“本轮”里，物品 i 被放了多次，这就变成了“完全背包”问题，而不是“0/1背包”了。

• 理论指南:
  • 文章讲解: 代码随想录-01背包理论基础(一维)
  • 视频讲解: B站视频-01背包(一维)

我的实现：一维 dp (滚动数组)

def knapsack_1d(M, N, weights, values):dp = [0] * (N + 1)for i in range(M): # 遍历物品# 关键：倒序遍历背包容量，保证每个物品只用一次for j in range(N, weights[i] - 1, -1):dp[j] = max(dp[j], dp[j - weights[i]] + values[i])return dp[N]

---

二、实战应用：将问题转化为 0/1 背包

3. LeetCode 416. 分割等和子集

题目描述: 给你一个 只包含正整数 的 非空 数组 nums。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

• 学习感悟: 这是一道非常精彩的 0/1 背包应用题。问题的转化是关键：

  1. 如果数组总和 total_sum 是奇数，那就不可能平分，直接返回 False。
  2. 如果 total_sum 是偶数，问题就转化为：能否从 nums 数组中，挑选出一些数，使它们的和恰好等于 target = total_sum / 2？
     这不就是一个背包问题吗！
  • 背包容量：target
  • 物品：nums 数组中的每一个元素 num
  • 物品的重量：num
  • 物品的价值：num
  • 问题: 能否把容量为 target 的背包装满？

• DP 定义: dp[j] (boolean) 表示容量为 j 的背包是否恰好能被装满。

• 状态转移: dp[j] = dp[j] or dp[j - num]。dp[j] 为 True 的条件是：它原来就是 True，或者，在不放 num 时 dp[j - num] 是 True（这样放入 num 之后 dp[j] 就能为 True）。

• 初始化: dp[0] = True，因为容量为 0 的背包，什么都不装，就算是被“装满”了。

• 资源包:

  • 题目/文章: https://programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html
  • 视频讲解: https://www.bilibili.com/video/BV1rt4y1N7jE

我的实现

class Solution:def canPartition(self, nums: List[int]) -> bool:total_sum = sum(nums)if total_sum % 2 != 0:return Falsetarget = total_sum // 2# dp[j]：容量为j的背包，能否被装满dp = [False] * (target + 1)# 初始化dp[0] = Truefor num in nums: # 遍历物品# 倒序遍历背包容量for j in range(target, num - 1, -1):dp[j] = dp[j] or dp[j - num]return dp[target]

总结

今天正式踏入了背包问题的世界，虽然只是 0/1 背包，但其深度和技巧性令我折服。二维 dp 的思想是基础，而一维 dp 的空间优化和倒序遍历的精髓，是理解背包问题的关键。更令我兴奋的是，学会了如何将一个看似无关的问题（如分割子集），巧妙地转化为背包模型来求解。这才是算法的魅力所在！