2025牛客多校第七场 双生、象牙 个人题解

G.双生

#质数筛 #欧拉筛 #数学

题目

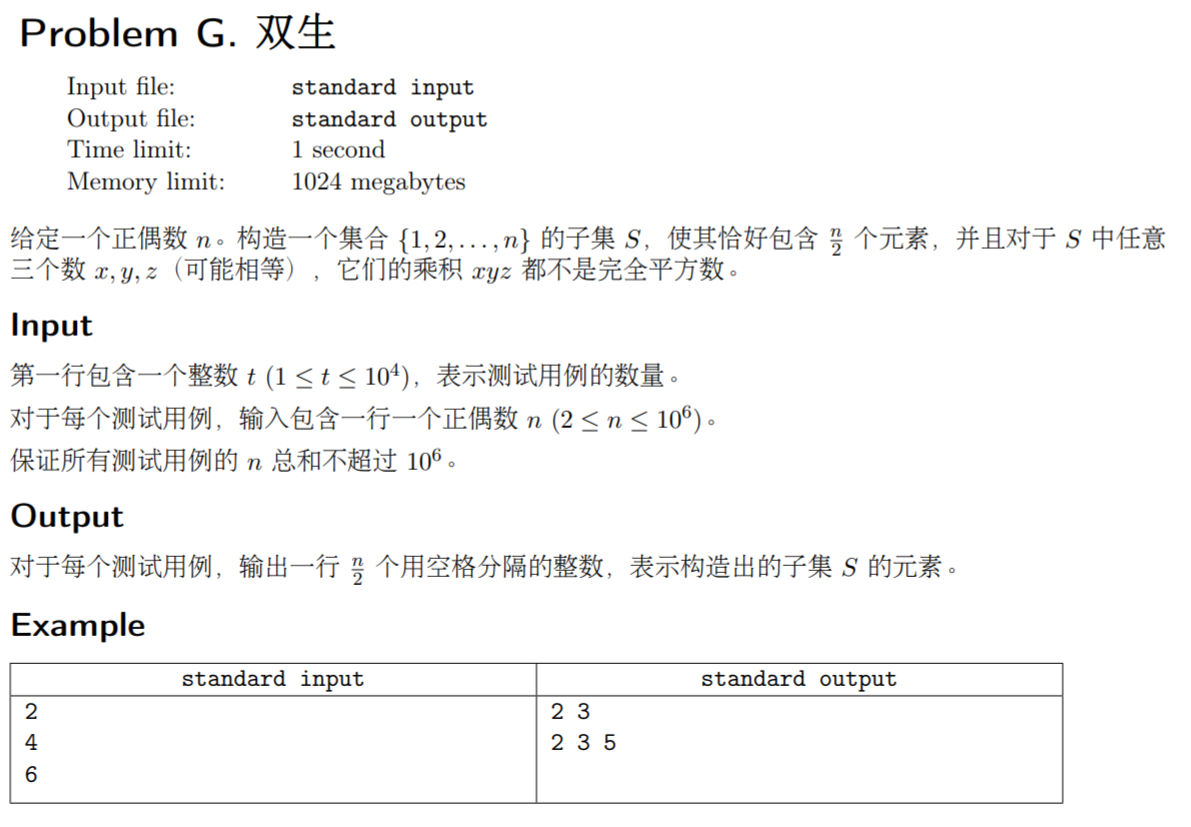
思路

要使$xyz$不是完全平方数，设$a=xyz=p_1^{q_1}{p}_2^{q_2}\dots p_k^{q_k}$，则有$\left({\sum }_{i=1}^k{q}_i\right)\%2=1$

为了方便计算，设$f(a)={\sum }_{i=1}^k{q}_i$，即让$f(a)\%2=1$

注意到$f(xy)=f(x)+f(y)$，则$f(a)=f(xyz)=f(x)+f(y)+f(z)$

若存在$f(x)$为偶，则可选取$f(y),f(z)$同为奇或同为偶使得$f(xyz)=0$，舍去

若不存在$f(x)$为偶，即$f(x)$为奇，那么$f(y),f(z)$必然也为奇，$f(xyz)=1$恒成立

因此题目便转换为了求$\frac{n}{2}$个$f(x)\%2=1$的数$x$，用欧拉筛$o(n)$预处理即可

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<numeric>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;
// #define int ll
constexpr ll  mod=998244353;vector<ll>prime,vis;
vector<bool>cnt;
void sieve(ll len) {vis.assign(len + 1, 0);prime.reserve(len+1);cnt.resize(len+1,0);prime.push_back(0);rep(i, 2, len) {if (!vis[i])prime.push_back(i);for (ll j = 1; i * prime[j] <= len&&j<prime.size(); j++) {vis[prime[j] * i] = 1;if (i % prime[j] == 0)break;}}rep(i,2,len){int cnt0=0,now=i;for(int j=1;prime[j]*prime[j]<=now;j++){while(now&&now%prime[j]==0)cnt0++,now/=prime[j];}if(now!=1)cnt0++;if(cnt0&1)cnt[i]=1;}
}void eachT() {int n;cin>>n;vector<int>ans;ans.reserve(n/2);rep(i,1,n)if((ans.size()<n/2)&&cnt[i])ans.push_back(i);see(ans);
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);ll t = 1;sieve(1e6+5);cin >> t;while (t--) { eachT(); }
}

---

J.象牙

#gcd #数学

题目

思路

看见本题的第一个思路便是想利用式子：
$$gcd(a^c,b^c)=gcd(a,b{)}^c$$
由于$gcd(a^b,c^d)$的幂次不尽相同，所以尝试主动构造相同的进行分布计算：
$$gcd(a^b,c^d)=gcd(a^{d+b-d},c^d)=gcd(a^d\times a^{b-d},c^d)$$
接下来便思考如何将$gcd$中的乘法分解开：
$$gcd(a\times b,c)=gcd(a,c)\times gcd\left(b,\frac{c}{gcd(a,c)}\right)$$
这实际上可以用容斥来理解，要求$a\times b$与$c$的公共部分，那么就等于$a$与$c$的公共部分再加上$b$与$c$的公共部分，再减去$a,b,c$的公共部分

因此带入上式：
$$\begin{array}{rl}gcd(a^d\times a^{b-d},c^d)& =gcd(a^d,c^d)\times gcd\left(a^{b-d},\frac{c^d}{gcd(a^d,c^d)}\right)\\ & \\ & =gcd(a,c{)}^d\times gcd\left(a^{b-d},{\left(\frac{c}{gcd(a,c)}\right)}^d\right)\end{array}$$
观察第二项$gcd$，又是一个形如$gcd(a^b,c^d)$的算式，因此可以通过递归求解

当$gcd(a,c)=1$时，原式退化为$gcd(a^{b-d},c^d)$，由$gcd$的交换性质，实际上这个式子可以一直使$gcd$中两个数的幂次不断减小，最终必然变为$gcd(a,c)$，答案即为1
因此$gcd(a,c)=1$即为终止条件

ps：本题卡常非常严重，赛时用函数递归一直在$TLE$，最终使用了$constexpr$加速以及迭代写法才最终过了…

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<numeric>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;
// #define int ll
constexpr ll  mod=998244353;
constexpr ll qpow(ll a,ll b){ll ans=1;a%=mod;while(b>0){if(b%2){ans*=a;ans%=mod;}a*=a;a%=mod;b>>=1;}return ans%mod;
}void eachT() {ll a,b,c,d;cin>>a>>b>>c>>d;ll ans=1;while(1){if(b==d){ans*=qpow(gcd(a,c),b);ans%=mod;break;}if(b>d){ll G=gcd(a,c);if(G==1)break;ans*=qpow(G,d);ans%=mod;c/=G;b-=d; }else{ll G=gcd(a,c);if(G==1)break;ans*=qpow(G,b);ans%=mod;a/=G;d-=b; }        }cout<<ans<<'\n';
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);ll t = 1;cin >> t;while (t--) { eachT(); }
}