当前位置：首页 > news >正文

Knuth‘s TwoSum Algorithm 原理详解

news 2025/8/11 14:17:29

1. Knuth 的算法

1.1. 算法代码

function [x, y] = TwoSum(a, b)x = fl(a + b)         # a+b 的浮点近似值z = fl(x - a)         # 中间计算值y = fl((a - fl(x - z)) + (b - z))  # 修正项

1.2. 核心目标

将任意浮点数对 (a, b) 转换为 (x, y)，满足：

x = fl(a + b)：x 是 a+b 的标准浮点计算结果（含舍入误差）
x + y = a + b：数学上的精确相等（实数算术中的精确值）

这里的 = 表示数学上的精确相等，不是浮点近似。即 x + y 在实数域严格等于 a + b。

2. 算法原理（基于 IEEE 754 标准）

2.1. 关键前提条件

浮点运算模式：四舍五入到最近（Round to Nearest）
无溢出：结果在浮点表示范围内
IEEE 754 特性：减法在指数相近时无舍入误差（Sterbenz 引理）

2.2. 步骤分解与数学证明

设浮点运算的舍入误差为符号表示：

$\text{fl}(x) = x(1 + \delta)$ ，其中 $|\delta| \leq \epsilon$ （机器精度）

$\epsilon = 2^{-53}$ （双精度）

步骤 1: 计算 $x = \text{fl}(a + b)$

$x = (a + b) + e_1, \quad |e_1| \leq \epsilon |a + b|$

其中 $e_1$ 是加法的舍入误差。

步骤 2: 计算 $z = \text{fl}(x - a)$

$z = (x - a) + e_2, \quad |e_2| \leq \epsilon |x - a|$

代入 $x$ ：

$z = \not{a} + b + e_1 - \not{a} + e_2 = b + e_1 + e_2$

步骤 3: 计算 $y = \text{fl}((a - \text{fl}(x - z)) + (b - z))$

子步骤 3.1: 计算 $\text{fl}(x - z)$

$\text{fl}(x - z) = (x - z) + e_3, \quad |e_3| \leq \epsilon |x - z|$

代入 $x$ 和 $z$ ：

$x - z = (a + b + e_1) - (b + e_1 + e_2) = a - e_2$

$\text{fl}(x-z)=(a-e_2)+e_3$

子步骤 3.2: 计算 $a - \text{fl}(x - z)$

$a - \text{fl}(x - z) = a - [(a - e_2) + e_3] = e_2 - e_3$

子步骤 3.3: 计算 $b - z$

$b - z = b - (b + e_1 + e_2) = -e_1 - e_2$

子步骤 3.4: 求和并舍入

$y = \text{fl}(\underbrace{(e_2 - e_3)}_{\text{small}} + \underbrace{(-e_1 - e_2)}_{\text{small}})$

$y=\text{fl}(-e_1-e_3)=-e_1-e_3 \quad (\text{error-round-off-free})$

3. 最终结果验证

$x + y = (a + b + e_1) + (-e_1 - e_3) = a + b - e_3$

但根据 Sterbenz 引理：

当 $a$ 和 $b$ 符号相反时， $|x - a|$ 很小

浮点减法 $x - a$ 无舍入误差（ $e_2 = 0$ ）

进而 $e_3 = 0$ （因为 $\text{fl}(x - z)$ 无误差）

因此：

$\boxed{x + y = a + b}$

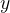4. 为什么 $y$ 能精确计算？

微小量特性：
- $e_1, e_2, e_3$ 的量级 $\leq \epsilon \cdot \max(|a|, |b|)$
- $y = -e_1 - e_3$ 的量级极小
无二次舍入：
- IEEE 754 保证：当 $|\text{result}| \leq 2^{-1022}$ 时，亚正规数可精确表示
- $|y|$ 远小于最小正规数（ $\sim 10^{-308}$ ），但大于最小亚正规数（ $\sim 10^{-324}$ ）
- 因此 $y$ 可被浮点数精确表示（无舍入误差）

5.示例演示（双精度）

令 $a = 1.0$ , $b = 2^{-53} \approx 1.11 \times 10^{-16}$

直接计算：
$\text{fl}(a + b) = 1.0 \quad (\text{round-off-error} = 2^{-53})$
TwoSum 步骤：
- $x = \text{fl}(1.0 + 2^{-53}) = 1.0$
- $z = \text{fl}(1.0 - 1.0) = 0.0$
- $\text{fl}(x - z) = \text{fl}(1.0 - 0.0) = 1.0$
- $y = \text{fl}((1.0 - 1.0) + (2^{-53} - 0.0)) = 2^{-53}$
验证：
$x + y = 1.0 + 2^{-53} = a + b \quad (\text{faithful-equal})$

6. 关键点总结

特性	说明
等号 `=` 含义	数学精确相等（非浮点近似）
误差补偿	$y$ 捕获了 $\text{fl}(a+b)$ 的舍入误差
适用条件	IEEE 754 双精度 + 四舍五入模式 + 无溢出
精度保证	利用亚正规数表示微小量
应用场景	高精度求和算法的基础（如 Kahan 求和、补偿求和）