从策略梯度到 PPO

在强化学习中，常用参数化策略 ${\pi }_{\theta }(a\mid s)$ 来表示智能体的行为策略。目标是最大化策略下的期望回报。

---

1. 轨迹与策略的概率分布

定义一个（随机）轨迹

$$\tau =(s_0,a_0,r_0,s_1,a_1,r_1,\dots ,s_T)$$

轨迹在参数化策略下的概率为

$$p_{\theta }(\tau )=p(s_0)\prod _{t=0}^{T-1}{\pi }_{\theta }(a_t\mid s_t)p(s_{t+1}\mid s_t,a_t).$$

其中环境动力学 $p(s_{t+1}\mid s_t,a_t)$ 与初始态分布 $p(s_0)$ 不依赖于 $\theta$。

定义轨迹的回报：

$$R(\tau )=\sum _{t=0}^{T-1}{\gamma }^t{r}_t,$$

策略的目标（期望回报）为：

$$J(\theta )={\mathbb{E}}_{\tau \sim p_{\theta }}[R(\tau )].$$

---

2. 对参数的梯度

对 $J(\theta )$ 求梯度：

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& ={\nabla }_{\theta }\int p_{\theta }(\tau )R(\tau )d\tau =\int R(\tau ){\nabla }_{\theta }{p}_{\theta }(\tau )d\tau \\ & =\int R(\tau )p_{\theta }(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )d\tau ={\mathbb{E}}_{\tau \sim p_{\theta }}[R(\tau ){\nabla }_{\theta }\log p_{\theta }(\tau )].\end{array}$$

该积分是勒贝格积分。展开 $\log p_{\theta }(\tau )$：

$$\log p_{\theta }(\tau )=\log p(s_0)+\sum _{t=0}^{T-1}(\log {\pi }_{\theta }(a_t\mid s_t)+\log p(s_{t+1}\mid s_t,a_t)).$$

因为 $p(s_0)$ 和 $p(s_{t+1}\mid s_t,a_t)$ 不依赖 $\theta$，它们的梯度为零，于是

$${\nabla }_{\theta }\log p_{\theta }(\tau )=\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t).$$

代入上式得：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim p_{\theta }}[R(\tau )\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)]=\sum _{t=0}^{T-1}{\mathbb{E}}_{\tau \sim p_{\theta }}[R(\tau ){\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)].$$

---

3. 用 reward-to-go / baseline 减少方差（REINFORCE→策略梯度定理）

把整个轨迹的总回报 $R(\tau )$ 替换为从时间 $t$ 开始的reward-to-go

$$G_t\triangleq \sum _{t^{\prime }=t}^{T-1}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}.$$
那么：
$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim p_{\theta }}[\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)G_t].$$

这是 REINFORCE 的无偏估计器，使用 $G_t$（而非整条轨迹回报）通常能显著降低方差，因为 $G_t$ 与在时间 $t$ 之前的动作无关。

为了进一步降低方差，可以引入 baseline $b(s_t)$（只依赖状态），利用恒等：

$$\begin{array}{rl}& {\mathbb{E}}_{a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)b(s_t)]\\ & =b(s_t){\mathbb{E}}_{a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)]\\ & =b(s_t)\int {\pi }_{\theta }(a_t\mid s_t){\nabla }_{\theta }log{\pi }_{\theta }(a_t\mid s_t)\\ & =b(s_t)\int {\nabla }_{\theta }{\pi }_{\theta }(a_t\mid s_t)\\ & =b(s_t){\nabla }_{\theta }{\mathbb{E}}_{a\sim {\pi }_{\theta }}{\pi }_{\theta }(a_t\mid s_t)\\ & =0.\end{array}$$

加入该项后：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim p_{\theta }}[\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)(G_t-b(s_t))].$$

常见的选择是$b(s_t)=V^{{\pi }_{\theta }}(s_t)$，定义优势函数：
$$A^{{\pi }_{\theta }}(s_t,a_t)=G_t-b(s_t)$$
将对轨迹$\tau$的采样转换为对每个时间步$t$对应的$(s_t,a_t)$的采样，那么：

$${\nabla }_{\theta }J(\theta )=\sum _t{\mathbb{E}}_{s_t\sim d^{{\pi }_{\theta }},a_t\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t\mid s_t)A^{{\pi }_{\theta }}(s_t,a_t)],$$

其中 $d^{{\pi }_{\theta }}$ 是策略 ${\pi }_{\theta }$ 下的状态访问分布.

---

4. 重要性采样(off policy)

在强化学习中，训练数据依赖于当前策略 ${\pi }_{\theta }$，参数更新后需要重新采样。为了复用旧策略 ${\pi }_{{\theta }^{\prime }}$ 收集的轨迹，可用重要性采样修正分布。

一般重要性采样公式：
$$E_{x\sim p(x)}[f(x)]=\int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=E_{x\sim q(x)}[f(x)\frac{p(x)}{q(x)}]$$
替换$\theta$为${\theta }^{\prime }$:
$$\begin{array}{rl}& {\mathbb{E}}_{s_t\sim d^{{\pi }_{\theta }},a_t\sim {\pi }_{\theta }}[A^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\\ & =\int p_{\theta }(s_t,a_t)[A^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\\ & =\int p_{{\theta }^{\prime }}(s_t,a_t)[\frac{p_{\theta }(s_t,a_t)}{p_{{\theta }^{\prime }}(s_t,a_t)}{A}^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\\ & =\int p_{{\theta }^{\prime }}(s_t,a_t)[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}\frac{p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(s_t)}{A}^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\end{array}$$

由于奖励函数的取值不会变化，即$A^{\theta }(s_t,a_t)=A^{{\theta }^{\prime }}(s_t,a_t)$，此外，假设$d^{{\pi }_{\theta }}$与$d^{{\pi }_{\theta }^{\prime }}$很接近，有$p_{\theta }(s_t)\approx p_{{\theta }^{\prime }}(s_t)$，那么，
$$\begin{array}{rl}& \int p_{{\theta }^{\prime }}(s_t,a_t)[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}\frac{p_{\theta }(s_t)}{p_{{\theta }^{\prime }}(s_t)}{A}^{\theta }(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\\ & \approx \int p_{{\theta }^{\prime }}(s_t,a_t)[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\nabla log{p}_{\theta }(a_t^n|s_t^n)]\\ & =\int p_{{\theta }^{\prime }}(s_t,a_t)[\frac{\nabla p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)]\end{array}$$
此时对应的优化目标是：
$$\begin{array}{rl}{J}^{{\theta }^{\prime }}(\theta )& =\sum _t{\mathbb{E}}_{s_t\sim d^{{\pi }_{{\theta }^{\prime }}},a_t\sim {\pi }_{\theta }^{\prime }}[\frac{p_{\theta }(a_t|s_t)}{p_{{\theta }^{\prime }}(a_t|s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)]\end{array}$$

---

5. PPO 的目标函数

设 ${\theta }^k$ 为收集数据时的旧参数，优势估计为 $A^{{\theta }^k}(s_t,a_t)$。

（A）带 KL 惩罚的形式

一种做法是在 surrogate 上加 KL 惩罚：

$$L^{\text{KL}}(\theta )=\sum _t{\mathbb{E}}_{s_t\sim d^{{\pi }_{\theta }},a_t\sim {\pi }_{\theta }}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }^k}(a_t\mid s_t)}{A}^{{\theta }^k}(s_t,a_t)]-\beta {\mathbb{E}}_{s\sim d^{{\pi }_{{\theta }^k}}}\left[\mathrm{KL}\right({\pi }_{{\theta }^k}(\cdot \mid s)\Vert {\pi }_{\theta }(\cdot \mid s)\left)\right]$$
通过调节 $\beta$ 控制新旧策略的距离.

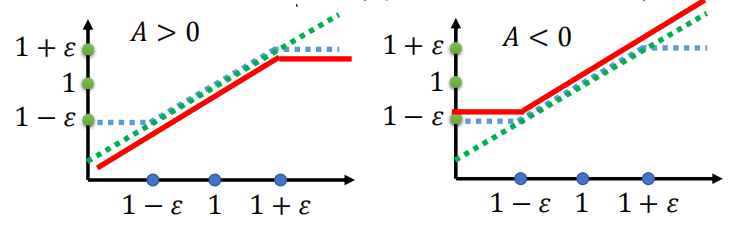
（B）裁剪（clipped）形式

PPO 中最常用的是裁剪目标（不显式计算 KL）：

$$L^{\text{CLIP}}(\theta )=\sum _t{\mathbb{E}}_{s_t\sim d^{{\pi }_{\theta }},a_t\sim {\pi }_{\theta }}\left[\min \right(r_t(\theta )A_t,\mathrm{clip}(r_t(\theta ),1-ϵ,1+ϵ)A_t\left)\right],$$

其中 $r_t(\theta )=\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }^k}(a_t\mid s_t)}$，$A_t$ 为 $A^{{\theta }^k}(s_t,a_t)$的简写。

裁剪的直观意义：当 $r_t(\theta )$ 在 $[1-ϵ,1+ϵ]$ 内，目标就和原始 surrogate 一致；当 $r_t$ 超出范围时，裁剪会限制它带来的收益，从而惩罚过大的策略更新，保证更新“近端”。