当前位置：首页 > news >正文

EP06：【DL 第二弹】动态计算图与梯度下降入门

news 2025/8/10 17:55:56

一、AutoGrad的回溯机制与动态计算图

在深度学习中，模型训练的核心是通过反向传播计算梯度，进而优化参数。PyTorch的AutoGrad模块正是实现这一过程的核心工具，其底层依赖回溯机制和动态计算图来自动追踪张量的计算过程，无需人工推导导数公式。理解这两个概念，是掌握PyTorch自动微分的基础。

1.1 可微分性

要让AutoGrad能够自动计算梯度，首先需要明确张量的可微分性——即哪些张量需要参与梯度计算，以及如何记录它们的运算关系。这涉及到张量的两个核心属性：requires_grad和grad_fn。

1.1.1 `requires_grad` 标记可微分张量

requires_grad是张量的一个布尔属性，用于标记该张量是否需要参与微分计算。当我们创建张量时，若设置requires_grad=True，则PyTorch会将其标记为可微分张量，并开始追踪所有以它为起点的运算。

为什么需要这个属性？因为在实际模型中，并非所有张量都需要计算梯度。例如，模型的输入数据（特征）通常不需要梯度（只需要用它们计算损失，不需要更新输入），而模型的参数（权重、偏置）则必须设置requires_grad=True，才能通过梯度下降更新。

t1 = torch.tensor(1., requires_grad=True)
print(t1)

运行结果：

tensor(1., requires_grad=True)

1.1.2 `grad_fn` 记录运算的回溯线索

grad_fn是如何追踪的记录者。它用于存储张量的微分函数，简单来说，就是记录当前张量是通过什么运算从其他张量得到的。更重要的是，由可微分张量计算得到的新张量，会自动继承可微分性，并生成对应的grad_fn。

# 构建可微分张量
t1 = torch.tensor(1., requires_grad=True)# 构建函数关系
y1 = t1**2
z1 = y1 + 1print(f"t1的微分函数：{t1.grad_fn}")
print(f"y1的微分函数：{y1.grad_fn}")
print(f"z1的微分函数：{z1.grad_fn}")

运行结果：

t1的微分函数：None
y1的微分函数：<PowBackward0 object at 0x0000021CC98ABF10>
z1的微分函数：<AddBackward0 object at 0x0000021CC98ABF10>

t1.grad_fn为None，因为它是手动创建的初始张量（不是由其他张量计算得到的）；而y1和z1的grad_fn分别记录了生成它们的运算，这正是AutoGrad回溯机制的基础——通过grad_fn，PyTorch能沿着运算链反向推导，从最终结果一步步找到初始张量的梯度。

1.2 计算图

基于requires_grad和grad_fn的回溯机制，PyTorch会将张量的计算过程抽象为张量计算图。它就像一张运算流程图，清晰记录了所有可微分张量之间的依赖关系，是反向传播的地图。

1.2.1 计算图的定义

计算图由节点和有向边组成：

节点：代表张量（包括输入张量、中间结果张量、输出张量）；
有向边：代表张量之间的运算关系（如加法、乘法、幂运算等）。

例如，对于计算过程x → y（x**2）→ z（y+1），对应的计算图中：

节点为x、y、z三个张量；
从x到y的边标记“幂运算（**2）”；
从y到z的边标记“加法运算（+1）”。

这张图的作用是记住整个计算过程：当我们需要计算z对x的梯度时，PyTorch可以沿着图中的边反向追溯，依次找到z对y的导数、y对x的导数，再通过链式法则得到最终结果。

1.2.2 计算图的节点类型

从功能上看，计算图中的节点可分为三类，理解它们的区别对梯度计算至关重要：

叶节点：计算的起点，即手动创建的可微分张量（如x = torch.tensor(1., requires_grad=True)）。叶节点没有grad_fn（因为它们不是由其他张量计算得到的），且只有叶节点的梯度会被反向传播直接保存（存储在grad属性中）。
中间节点：由叶节点计算得到，但不是最终输出的张量（如1.2.1的y）。中间节点的requires_grad为True，且有grad_fn，但默认情况下，它们的梯度在反向传播后会被自动释放（节省内存），若需保存需调用retain_grad()。
输出节点：计算过程的最终结果张量（如1.2.1的z）。输出节点是反向传播的起点，我们通过调用其backward()方法触发梯度计算。

一个更具体的例子：设x = torch.tensor(2., requires_grad=True)，y = x * 3，z = y + 5。则计算图中：

叶节点是x（初始输入，无grad_fn）；
中间节点是y（由x计算得到，grad_fn为<MulBackward0>）；
输出节点是z（最终结果，grad_fn为<AddBackward0>）。

通过这张图，PyTorch能清晰知道“从z到x需要经过乘法和加法两步运算”，从而准确计算梯度。

1.2.3 计算图的动态性

PyTorch的计算图是动态计算图，这是它与早期TensorFlow（静态计算图）的核心区别，也是其灵活性的关键。

动态计算图的动态体现在：计算图会随着张量的运算实时创建和更新。例如，当我们先定义x = torch.tensor(1., requires_grad=True)，y = x**2时，计算图只有x→y的关系；当我们再定义z = y+1时，计算图会立即更新为x→y→z。这种边算边画的特性，让我们可以像写普通Python代码一样构建复杂的计算逻辑。

而静态计算图（如早期TensorFlow）需要先定义图，再运行图，例如，先定义x、y = x**2、z = y+1的关系，再通过sess.run()执行计算。这种方式不够灵活，尤其在需要根据中间结果调整运算逻辑时（如循环次数依赖计算结果），动态图的优势会非常明显。

动态计算图的灵活性让PyTorch更适合科研实验和快速原型开发，这也是它在学术界广泛流行的重要原因之一。

二、反向传播与梯度计算

反向传播是深度学习中计算梯度的核心方法，它利用计算图的回溯机制，从输出节点出发，沿着计算图反向推导叶节点的梯度。理解反向传播的原理、注意事项和控制方法，是正确使用AutoGrad的关键。

2.1 反向传播的基本过程

反向传播的本质是沿着计算图反向传递函数关系，通过链式法则求解叶节点的梯度。在PyTorch中，我们可以通过张量的backward()方法直接触发这一过程。

t1 = torch.tensor(1., requires_grad=True)
y1 = t1**2
z1 = y1 + 2print(f"t1的导数值：{t1.grad}")
print(f"z1：{z1}")
print(f"z1的微分函数：{z1.grad_fn}")# 反向传播
z1.backward()
print(f"t1的导数值：{t1.grad}")# ×1. 不可以进行第二次反向传播
"""
z1.backward()
print(f"t1的导数值：{t1.grad}")
"""
# RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward

运行结果：

t1的导数值：None
z1：3.0
z1的微分函数：<AddBackward0 object at 0x00000248935D12D0>
t1的导数值：2.0

示例解读：

我们可以手动推导验证：

z1 = y1 + 2，而y1 = t1** 2，因此z1 = t1 **2 + 2；
根据求导公式，z1对t1的导数为2*t1；
当t1=1时，导数为2*1=2，与PyTorch计算结果一致。

PyTorch的反向传播过程其实就是模拟了这一推导：

从输出节点z1出发，通过z1.grad_fn（<AddBackward0>）找到上一步运算（z1 = y1 + 2），计算z1对y1的导数（结果为1）；
再通过y1.grad_fn（<PowBackward0>）找到更上一步运算（y1 = t1** 2），计算y1对t1的导数（结果为2*t1）；
最后通过链式法则，将两个导数相乘（1*2*t1），得到z1对t1的导数（即2*t1），并保存到t1.grad中。

2.2 反向传播的注意事项

反向传播的结果受起点（哪个张量调用backward()）、中间节点梯度是否保存、梯度是否累加等因素影响，稍不注意就可能得到错误结果或触发报错。

2.2.1 反向传播的一次性特性

需要注意的是，反向传播默认只能执行一次。如果尝试第二次调用z1.backward()，会报错。

# 第二次反向传播（会报错）
z1.backward()  # 报错：RuntimeError: Trying to backward through the graph a second time...

这是因为反向传播后，为了节省内存，PyTorch会自动释放中间节点的梯度和计算图信息。如果需要多次反向传播（如某些复杂模型训练场景），可以在第一次调用时设置retain_graph=True，保留计算图。

z1.backward(retain_graph=True)  # 第一次反向传播，保留计算图
z1.backward()  # 第二次反向传播，此时可正常执行

但需注意，保留计算图会增加内存占用，非必要时不建议使用。

2.2.2 中间节点与输出节点的区别

反向传播计算的是起点张量对叶节点的导数，因此起点不同（输出节点或中间节点），得到的梯度结果也不同。因此，反向传播的起点必须是我们关心的最终结果（通常是损失函数），否则得到的梯度没有实际意义。

t2 = torch.tensor(1., requires_grad=True)
y2 = t2**2
z2 = y2**2
print(f"t2的导数值：{t2.grad}")
z2.backward()
print(f"t2的导数值：{t2.grad}")t2 = torch.tensor(1., requires_grad=True)
y2 = t2**2
z2 = y2**2
print(f"t2的导数值：{t2.grad}")
y2.backward()
print(f"t2的导数值：{t2.grad}")

运行结果：

t2的导数值：None
t2的导数值：4.0
t2的导数值：None
t2的导数值：2.0

2.2.3 中间节点的梯度保存

默认情况下，反向传播只会保存叶节点的梯度，中间节点的梯度会被自动释放（节省内存）。如果需要查看中间节点的梯度（如分析模型中间层的梯度变化），需调用retain_grad()手动开启保存。

t3 = torch.tensor(1., requires_grad=True)
y3 = t3**2
y3.retain_grad()
z3 = y3**2
z3.backward()
print(f"t3的导数值：{t3.grad}")
print(f"y3的导数值：{y3.grad}")

运行结果：

t3的导数值：4.0
y3的导数值：2.0

示例解读：

y3.grad=2.0的原因是：z = y3**2，其对y3的导数为2*y3，而y3=1**2=1，因此结果为2*1=2。

2.2.4 梯度的累加性与清零操作

若多次反向传播且未清空梯度，叶节点的梯度会自动累加（即新梯度 = 旧梯度 + 新计算的梯度）。这一特性在某些场景下有用（如累积多个批次的梯度再更新），但在常规迭代优化中可能导致错误。

x = torch.tensor(1., requires_grad=True)
y = x**2
y.backward(retain_graph=True)
print(x.grad)  # 第一次：2.
y.backward()
print(x.grad)  # 第二次：4.（2+2）x.grad.zero_()
y.backward()
print(x.grad)  # 重置后：2.

示例解读：

在模型训练中，每次迭代（如每个批次）都需要计算新的梯度并更新参数，因此必须在每次反向传播前用x.grad.zero_()清空旧梯度，否则累加的梯度会导致参数更新错误。

2.3 阻止计算图的追踪

在某些场景下（如模型推理、验证），我们不需要追踪张量的运算（可节省内存和计算资源）。PyTorch提供了两种常用方法来阻止计算图追踪：with torch.no_grad()上下文管理器和detach()方法。

2.3.1 `with torch.no_grad()` 临时屏蔽追踪

with torch.no_grad()会创建一个上下文环境，在该环境内的所有张量运算都不会被AutoGrad追踪，即新生成的张量requires_grad会被强制设为False，且grad_fn为None。

该方法适合临时屏蔽部分运算的追踪，比如在验证模型时，不需要计算梯度，可将整个验证过程放在with torch.no_grad()中。

t4 = torch.tensor(1., requires_grad=True)
y4 = t4**2
with torch.no_grad():z4 = y4**2
print(f"z4：{z4}")
print(f"z4的微分函数：{z4.grad_fn}")
print(f"y4的微分函数：{y4.grad_fn}")

运行结果：

z4：1.0
z4的微分函数：None
y4的微分函数：<PowBackward0 object at 0x00000248935D12D0>

示例解读：

y4在环境外仍被正常追踪，而z4在环境内被屏蔽，这在验证模型时非常实用——此时我们只需要前向计算预测结果，不需要计算梯度，可大幅节省内存。

2.3.2 `detach()` 创建不可导的副本

detach()方法会返回一个与原张量数值相同，但不再被计算图追踪的新张量（即requires_grad=False，grad_fn=None）。原张量的追踪不受影响。

detach()的核心作用是切断梯度传递——若模型某部分参数不需要更新（如预训练模型的特征提取层），可通过detach()阻止其梯度被计算，从而固定参数。

该方法适合需要复用张量数值但不追踪其来源的场景，比如在迁移学习中，固定预训练模型的参数时，可通过detach()阻断梯度传递。

t5 = torch.tensor(1., requires_grad=True)
y5 = t5**2
y5_ = y5.detach()
z5 = y5_**2
print(f"y5的微分函数：{y5.grad_fn}")
print(f"z5的微分函数：{z5.grad_fn}")

运行结果：

y5的微分函数：<PowBackward0 object at 0x00000248935D12D0>
z5的微分函数：None

2.4 叶节点的识别

叶节点是计算图的起点，只有叶节点的梯度会被反向传播直接保存（非叶节点的梯度需手动开启保存）。因此，准确识别叶节点对理解梯度计算至关重要。

2.4.1 叶节点的识别标准

可以通过张量的is_leaf属性判断其是否为叶节点，规则如下：

手动创建的张量（未经过任何运算）是叶节点：无论requires_grad是否为True，只要是直接创建的（如torch.tensor(1.)或torch.tensor(1., requires_grad=True)），都是叶节点。
由其他张量计算得到的张量（中间节点/输出节点）不是叶节点：例如y = x**2，y是通过x计算得到的，因此y.is_leaf=False。
通过detach()得到的张量是叶节点：detach()会切断张量与计算图的联系，使其成为新的“起点”，因此y_detach.is_leaf=True。

t6 = torch.tensor(1., requires_grad=True)
y6 = t6**2
z6 = y6**2
print(f"t6是否是叶结点：{t6.is_leaf}")
print(f"y6是否是叶结点：{y6.is_leaf}")
print(f"z6是否是叶结点：{z6.is_leaf}")# *1. 任何一个新创建的张量都可以是叶结点
t7 = torch.tensor(1., requires_grad=True)
print(f"t7是否是叶结点：{t7.is_leaf}")# *2. 经过detach的张量也可以叶结点
t8 = torch.tensor(1., requires_grad=True)
t8_ = t8.detach()
print(f"t8_是否是叶结点：{t8_.is_leaf}")

运行结果：

t6是否是叶结点：True
y6是否是叶结点：False
z6是否是叶结点：False
t7是否是叶结点：True
t8_是否是叶结点：True

2.4.2 叶节点的识别意义

叶节点的核心意义在于：反向传播中，只有叶节点的grad属性会被自动赋值。非叶节点的grad默认为空（除非调用retain_grad()）。

在模型训练中，模型的参数（权重、偏置）都是叶节点（手动创建且requires_grad=True），因此它们的梯度会被自动保存，供后续优化器更新；而中间层的输出张量（非叶节点）的梯度默认不保存，避免占用过多内存。

三、梯度下降的基本思想

梯度下降是深度学习中优化模型参数的核心方法，它通过迭代逐步逼近损失函数的最小值，解决了最小二乘法等解析方法的局限性。理解梯度下降的思想，是掌握模型训练逻辑的基础。

3.1 最小二乘法的局限与优化

在机器学习中，最小二乘法是求解线性回归参数的经典方法，但它存在严格的前提条件，在许多实际场景中会失效，而梯度下降正是解决这一问题的通用方案。

3.3.1 最小二乘法的原理与局限

最小二乘法的核心是通过最小化残差平方和求解参数。对于线性回归模型y = Xw + b（其中X是特征矩阵，w是权重，b是偏置），其参数的解析解为：
$w^T=(XTX)−1XTy \hat{w}^T = (X^TX)^{-1}X^Ty$
其中 $w^\hat{w}$ 是包含w和b的参数向量， $X$ 是添加了全为1的列（对应偏置b）的特征矩阵， $y$ 是标签向量。

但该公式成立的前提是： $X^TX$ 必须是可逆矩阵（即满秩）。在实际场景中，这一条件常被打破：

特征多重共线性：若特征之间存在线性相关（如面积和体积高度相关）， $X^TX$ 的行列式为0，不可逆；
样本数少于特征数：若样本数m < 特征数d， $X^TX$ 是d×d矩阵，其秩最大为m < d，必然不可逆（如2个样本、3个特征时， $X^TX$ 秩≤2 < 3）。

此时，最小二乘法无法直接求解参数。

3.3.2 岭回归的妥协

为解决 $X^TX$ 不可逆的问题，岭回归通过添加正则项（扰动项） $λI\lambda I$ （ $λ\lambda$ 为正数， $I$ 为单位矩阵），使 $XTX+λIX^TX + \lambda I$ 一定可逆：
$w^T∗=(XTX+λI)−1XTy \hat{w}^{T*} = (X^TX + \lambda I)^{-1}X^Ty$

但是，岭回归得到的是近似最优解，而非最小二乘法的精确最优解，且 $λ\lambda$ 的选择需要人工调参，不够灵活。

3.3.3 梯度下降的优势

相比之下，梯度下降的优势在于：

无需矩阵可逆：它通过迭代逐步逼近最优解，不依赖 $X^TX$ 的可逆性；
适用范围广：不仅适用于线性模型，还能优化非线性、非凸的复杂损失函数（如神经网络的损失函数）；
灵活性高：可通过调整学习率、迭代次数等参数控制优化过程。

因此，当解析方法失效时，梯度下降成为更通用的选择。

3.2 梯度下降的核心思想

梯度下降的核心思想可以用盲人下山来比喻：盲人站在山上（初始参数），每次向最陡的下坡方向走一小步（参数更新），不断重复，最终逼近山脚（最优解）。

3.2.1 数学描述

对于目标函数 $L (w)$ （如损失函数， $w$ 为参数），梯度下降的步骤如下：

随机初始化参数：选择初始点 $w_0$ （相当于盲人随机站在山上某点）；
计算梯度：求 $L (w)$ 在 $w_0$ 处的梯度 $∇L(w0)\nabla L(w_0)$ （梯度方向是函数上升最快的方向，反方向是下降最快的方向）；
更新参数：沿梯度反方向移动， $w1=w0−α∇L(w0)w_1 = w_0 - \alpha \nabla L(w_0)$ （ $α\alpha$ 为步长，即学习率）；
重复迭代：直到参数变化足够小（收敛）或达到最大迭代次数。

3.2.2 案例解析

以简单线性回归为例：假设我们要拟合方程 $y = a x + b$ ，给定样本 $(1, 2)$ 和 $(3, 4)$ ，损失函数为残差平方和 $SSE(a,b) = (2 - a - b)^2 + (4 - 3a - b)^2$ ，目标是找到 $a$ 和 $b$ 使 $SSE$ 最小（最优解为 $a = 1, b = 1$ ）。

用梯度下降求解的过程：

初始参数：设 $a = 0, b = 0$ （随机初始点）；
计算梯度：
- $SSE$ 对 $a$ 的偏导数： $∂SSE∂a=2(2−a−b)(−1)+2(4−3a−b)(−3)\frac{\partial SSE}{\partial a} = 2(2 - a - b)(-1) + 2(4 - 3a - b)(-3)$ ，代入 $a = 0, b = 0$ 得 $- 28$ ；
- $SSE$ 对 $b$ 的偏导数： $∂SSE∂b=2(2−a−b)(−1)+2(4−3a−b)(−1)\frac{\partial SSE}{\partial b} = 2(2 - a - b)(-1) + 2(4 - 3a - b)(-1)$ ，代入 $a = 0, b = 0$ 得 $- 12$ ；
  因此梯度为 $(- 28, - 12)$ 。
更新参数：取学习率 $α=0.01\alpha=0.01$ ，沿梯度反方向移动：
- 新 $a = 0 - 0.01 \times (- 28) = 0.28$ ；
- 新 $b = 0 - 0.01 \times (- 12) = 0.12$ ；
验证效果：新参数下的 $SSE = (2 - 0.28 - 0.12)^2 + (4 - 3×0.28 - 0.12)^2 = 11.8016$ ，比初始 $SSE = 20$ 更小，确实下降。

# step 1：初始随机点
x1 = torch.tensor(0., requires_grad=True)
y1 = torch.tensor(0., requires_grad=True)
# step 2：计算梯度
S1 = torch.pow((2 - x1 - y1), 2) + torch.pow((4 - 3*x1 - y1), 2)
# step 3：反向传播
S1.backward()
# step 4：打印结果
print(f"x1的导数：{x1.grad}")
print(f"y1的导数：{y1.grad}")

运行结果：

x1的导数：-28.0
y1的导数：-12.0

示例解读：

结果与手动推导一致，验证了梯度计算的正确性。通过多次迭代，参数会逐步逼近 $(1, 1)$ ，这就是梯度下降小步快跑逼近最优解的核心逻辑。

3.3 梯度下降的方向与步长

梯度下降的效果由两个关键因素决定：方向（往哪走）和步长（走多远）。两者的选择直接影响收敛速度和能否找到最优解。

3.3.1 方向：梯度的反方向

梯度（导数）的物理意义是函数在某点的最陡上升方向，因此其反方向就是最陡下降方向——沿此方向移动，函数值下降最快。

一元函数：例如， $f(x) = x^2$ ，在 $x = 1$ 处的导数为2（梯度为2），说明沿 $x$ 正方向函数上升最快，因此反方向（ $x$ 负方向）是下降最快的方向。
多元函数：例如，损失函数 $SSE (a, b)$ ，在 $(a = 0, b = 0)$ 处的梯度为 $(- 28, - 12)$ ，其反方向 $(28, 12)$ 是 $SSE$ 下降最快的方向。这一方向可通过梯度向量的比例确定（如 $a$ 和 $b$ 的更新比例为28:12=7:3）。

需要注意的是，梯度方向会随参数变化而变化。每次更新参数后，函数在新点的最陡方向会改变，因此必须重新计算梯度。

# step 5：确定原点移动方向
x_ = np.arange(-30, 30, 0.1)
y_ = (12/28)*x_
plt.plot(x_, y_, '-')
plt.plot(0, 0, 'ro')
plt.plot(x1.grad.item(), y1.grad.item(), 'go')
plt.show()

运行结果：

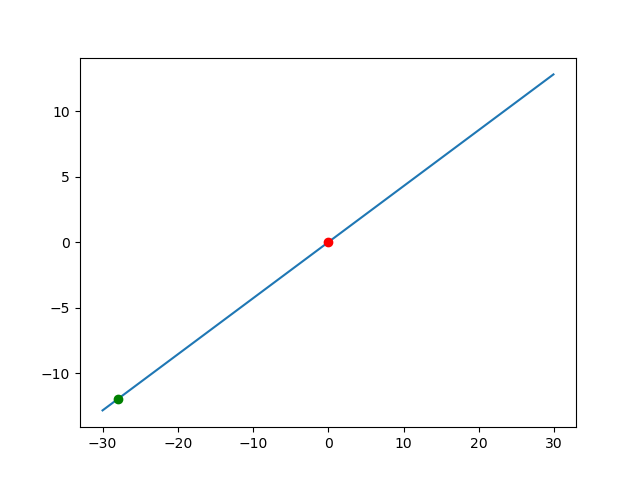
3.3.2 步长：学习率的选择

步长由学习率 $α\alpha$ 控制，它决定了每次迭代的移动距离。步长选择不当会导致两种问题：

步长太小：收敛速度慢。例如，若 $α=0.0001\alpha=0.0001$ ，从 $(0, 0)$ 到 $(1, 1)$ 可能需要数万次迭代，效率极低；
步长太大：可能跳过最优解，导致震荡。例如，对 $SSE (a, b)$ ，若 $α=0.5\alpha=0.5$ ，第一次更新后 $a = 0 - 0.5 \times (- 28) = 14$ ， $b = 0 - 0.5 \times (- 12) = 6$ ，此时 $SSE$ 会急剧增大，后续迭代可能在最优解附近来回波动，无法收敛。

学习率的选择没有固定标准，通常需要根据问题调整（如从0.01开始尝试）。在上述 $SSE (a, b)$ 的例子中， $α=0.01\alpha=0.01$ 是较合适的选择：每次移动一小步，逐步逼近最优解。

# step 6：移动
x1_ = x1 - 0.01*x1.grad
y1_ = y1 - 0.01*y1.grad
x1_.retain_grad()
y1_.retain_grad()
S1_ = torch.pow((2 - x1_ - y1_), 2) + torch.pow((4 - 3*x1_ - y1_), 2)
S1_.backward()
print(f"x1_的导数：{x1_.grad}")
print(f"y1_的导数：{y1_.grad}")

运行结果：

x1_的导数：-21.440000534057617
y1_的导数：-9.279999732971191

总结来说，梯度下降的核心逻辑是：沿梯度反方向，以合适的步长逐步移动，直到逼近最优解。

四、梯度下降的数学表示

4.1 梯度下降的代数表示

以多元线性回归模型为例，我们需要通过梯度下降求解参数，使损失函数最小。

4.4.1 模型与损失函数定义

多元线性回归模型为：
$f(x) = w_1x_1 + w_2x_2 + ... + w_dx_d + b$
其中 $w_1,...,w_d$ 是特征权重， $b$ 是偏置， $x_1,...,x_d$ 是输入特征。

损失函数通常定义为均方误差的一半（除以2是为了求导时抵消系数，简化计算）：
$L(w_1,...,w_d,b) = \frac{1}{2m}\sum_{j=1}^m (f(x^{(j)}) - y_j)^2$
其中 $m$ 是样本数， $x^{(j)}=(x_1^{(j)},...,x_d^{(j)})$ 是第 $j$ 个样本的特征， $y_j$ 是第 $j$ 个样本的标签， $f(x^{(j)})$ 是模型对第 $j$ 个样本的预测值。

4.4.2 梯度计算与参数更新

梯度下降的核心是计算损失函数对每个参数的偏导数（梯度），并沿反方向更新参数。

（1）计算梯度

对权重 $w_i$ ：
$∂L∂wi=1m∑j=1m(f(x(j))−yj)xi(j)\frac{\partial L}{\partial w_i} = \frac{1}{m}\sum_{j=1}^m (f(x^{(j)}) - y_j)x_i^{(j)}$
（推导：对 $L$ 求导，链式法则展开后， $12m×2∑(...)=1m∑(...)\frac{1}{2m}×2\sum(...) = \frac{1}{m}\sum(...)$ ）
对偏置 $b$ （可视为 $x_0=1$ 的权重）：
$∂L∂b=1m∑j=1m(f(x(j))−yj)\frac{\partial L}{\partial b} = \frac{1}{m}\sum_{j=1}^m (f(x^{(j)}) - y_j)$

（2）参数更新

沿梯度反方向更新所有参数：
$wi=wi−α⋅∂L∂wiw_i = w_i - \alpha \cdot \frac{\partial L}{\partial w_i}$

$\alpha \cdot \frac{\partial L}{\partial b}$
其中 $α\alpha$ 是学习率（步长）。

4.4.3 迭代停止条件

达到预设的最大迭代次数（如1000次）；
参数更新量小于阈值（如 $w_i^{new} - w_i^{old}| < 1e-6$ ）；
损失函数的变化量小于阈值（如 $L_{new} - L_{old}| < 1e-6$ ）。

4.2 步长的深入理解

步长（学习率 $α\alpha$ ）的作用可以通过一元函数的例子直观理解，它决定了参数向最优解靠近的速度和稳定性。

以简单的线性回归为例：数据集 ${(1,2),(2,4),(3,6)\}$ ，用 $y = w x$ 拟合，损失函数为：
$SSE(w) = (2 - w)^2 + (4 - 2w)^2 + (6 - 3w)^2 = 14w^2 - 56w + 56$
其梯度（导数）为：
$\frac{\partial SSE}{\partial w} = 28w - 56$
最优解为梯度为0的点：
$28 w - 56 = 0 \to w = 2$

设初始 $w_0=0$ ，观察不同 $α\alpha$ 下的迭代：

4.2.1 $α=0.5\alpha=0.5$

第1轮：梯度 $= 28 \times 0 - 56 = - 56$ ， $w_1=0 - 0.5×(-56)=28×0.5=1$
第2轮：梯度 $= 28 \times 1 - 56 = - 28$ ， $w_2=1 - 0.5×(-28)=1 + 14=15$

显然远离最优解，说明原示例 $α=0.5\alpha=0.5$ 过大，正确合适步长应为更小值，如 $α=0.1\alpha=0.1$ 。

4.2.2 $α=0.1\alpha=0.1$

第1轮： $w_1=0 - 0.1×(-56)=5.6$
第2轮：梯度 $= 28 \times 5.6 - 56 = 156.8 - 56 = 100.8$ ， $w_2=5.6 -0.1×100.8=5.6-10.08=-4.48$

发现仍有问题，实际该函数为凸函数，学习率需更小，如 $α=0.01\alpha=0.01$ 。

4.2.3 $α=0.01\alpha=0.01$

第1轮： $w_1=0 -0.01×(-56)=0.56$ ；
第2轮：梯度 $= 28 \times 0.56 - 56 = 15.68 - 56 = - 40.32$ ， $w_2=0.56 -0.01×(-40.32)=0.56+0.4032=0.9632$ ；
第3轮：梯度 $= 28 \times 0.9632 - 56 \approx 26.9696 - 56 = - 29.0304$ ， $w_3≈0.9632 +0.2903≈1.2535$ ；

逐步逼近 $w = 2$ 。

4.2.4 $α=2\alpha=2$

第1轮： $w_1=0 -2×(-56)=112$ ；
第2轮：梯度 $= 28 \times 112 - 56 = 3136 - 56 = 3080$ ， $w_2=112 -2×3080=112-6160=-6048$ ；

参数远离最优解，无法收敛。

可见，步长的本质是每次移动的距离比例，需根据函数的陡峭程度调整——函数越陡峭（梯度绝对值越大），步长应越小，避免跳过最优解。

4.3 梯度下降的矩阵表示

代数表示适合理解，但在代码中用矩阵运算更高效（尤其对大规模数据）。通过矩阵表示，梯度下降的计算可简化为矩阵操作，避免循环。

4.3.1 矩阵定义

参数向量： $w^=(w1,w2,...,wd,b)\hat{w} = (w_1, w_2, ..., w_d, b)$ （包含所有权重和偏置，形状为 $1 \times (d + 1)$ ）；
特征矩阵： $X$ （形状为 $m \times (d + 1)$ ），每行是 $x_1^{(j)}, x_2^{(j)}, ..., x_d^{(j)}, 1)$ （最后一列全为1，对应偏置 $b$ 的系数）；
标签向量： $y$ （形状为 $m \times 1$ ），包含所有样本的标签。

4.3.2 损失函数与梯度的矩阵形式

模型预测值为 $X⋅w^TX \cdot \hat{w}^T$ （矩阵乘法，形状为 $m \times 1$ ），损失函数的矩阵表示为：
$L(w^)=12m(y−Xw^T)T(y−Xw^T) L(\hat{w}) = \frac{1}{2m}(y - X \hat{w}^T)^T(y - X \hat{w}^T)$
（ $(y−Xw^T)T(y - X \hat{w}^T)^T$ 是行向量，与列向量 $(y−Xw^T)(y - X \hat{w}^T)$ 相乘得到标量）

梯度的矩阵表示（对 $w^\hat{w}$ 求导）：
$∂L∂w^=1mXT(Xw^T−y) \frac{\partial L}{\partial \hat{w}} = \frac{1}{m}X^T(X \hat{w}^T - y)$
（推导：通过矩阵求导法则展开，结果为行向量，形状为 $1 \times (d + 1)$ ）

4.3.3 参数更新的矩阵形式

参数更新公式为：
$w^=w^−α⋅∂L∂w^ \hat{w} = \hat{w} - \alpha \cdot \frac{\partial L}{\partial \hat{w}}$
代入梯度表达式：
$w^=w^−αmXT(Xw^T−y) \hat{w} = \hat{w} - \frac{\alpha}{m}X^T(X \hat{w}^T - y)$

4.3.4 矩阵表示的优势

矩阵表示的核心优势是计算高效：PyTorch等框架对矩阵运算（如torch.mm矩阵乘法、torch.t转置）进行了深度优化，可利用GPU并行计算，大幅提升大规模数据下的运算速度。相比之下，代数表示的循环实现（逐样本计算梯度）在大数据集上会非常缓慢。

五、梯度下降的手动实现

基于上述矩阵表示，我们可以手动实现梯度下降算法。以简单线性回归为例，展示从数据准备、参数初始化到迭代优化的完整过程，帮助理解框架中优化器的底层逻辑。

5.1 问题定义

我们要拟合如下线性方程组（目标是找到 $a = 1, b = 1$ 的最优解）：
$\cdot a + b = 2$

$\cdot a + b = 4$
其中 $a$ 是特征权重， $b$ 是偏置，可统一表示为参数向量 $w^=(a,b)\hat{w} = (a, b)$ 。

5.2 数据与参数初始化

特征矩阵 $X$ ：包含两个样本，每行是 $(x, 1)$ （ $x$ 为自变量，1对应截距 $b$ ）：
```
X = torch.tensor([[1., 1], [3, 1]], requires_grad=True)
```

标签向量

y

：

y = torch.tensor([2., 4], requires_grad=True).reshape(2, 1)

初始参数 $w^=(a,b)T\hat{w} = (a, b)^T$ ：初始化为全0：
```
weights = torch.zeros(2, 1, requires_grad=True)
```

学习率

α=0.01\alpha = 0.01

：

eps = torch.tensor(0.01, requires_grad=True)

5.3 单轮迭代过程

计算梯度：根据矩阵公式 $∂L∂w^=1mXT(Xw^T−y)\frac{\partial L}{\partial \hat{w}} = \frac{1}{m}X^T(X \hat{w}^T - y)$ （ $m = 2$ ）：
```
# 计算预测值与标签的误差：X@weights - y
error = torch.mm(X, weights) - y
# 计算梯度
grad = torch.mm(X.t(), error) / 2  # X.t()是X的转置，mm是矩阵乘法
```
初始时， $weights=(0,0)^T$ ， $X@weights=(0,0)^T$ ，误差 $2, -4)^T$ ，梯度计算为：
$\frac{1}{2} \begin{bmatrix}1 & 3 \\ 1 & 1\end{bmatrix} \begin{bmatrix}-2 \\ -4\end{bmatrix} = \frac{1}{2} \begin{bmatrix}-14 \\ -6\end{bmatrix} = \begin{bmatrix}-7 \\ -3\end{bmatrix}$
更新参数： $\alpha \cdot grad$ ：
```
weights = weights - eps * grad
```
代入值： $weights = (0,0)^T - 0.01×(-7,-3)^T = (0.07, 0.03)^T$ 。

5.4 多轮迭代与收敛

通过循环执行上述步骤，参数会逐步逼近最优解。定义迭代函数：

def Grad_Descent(X, y, eps = torch.tensor(0.01, requires_grad = True), max_iter = 1000):m, n = X.shapeweights = torch.zeros(n, 1, requires_grad = True)for k in range(max_iter):grad = torch.mm(X.t(), (torch.mm(X, weights) - y))/2weights = weights - eps * gradreturn weightsweights = Grad_Descent(X, y)
print(f"weights：{weights}")SSE = torch.mm((torch.mm(X, weights) - y).t(), (torch.mm(X, weights) - y))
print(f"SSE：{SSE}")